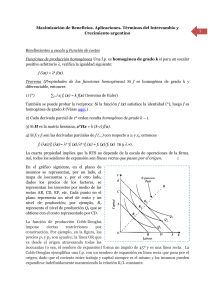
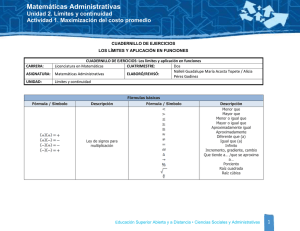
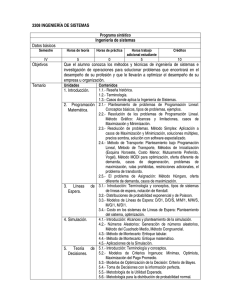
La Maximización del Beneficio Π = + + − − p y p y w x w x L L
Anuncio

Beneficios = Ingresos menos Costes La empresa usa factores j = 1…,m para producir bienes i = 1,…n. La Maximización del Beneficio Niveles de producción son y1,…,yn. Niveles de factores son x1,…,xm. Precios de los bienes son p1,…,pn . (dados) Precios (coste de oportunidad) de los factores son w1,…,wm. (dados) Π = p1y1 +L+ pnyn − w 1x1 −L w mxm . Flujos de ingresos y costes Maximización de beneficios a corto y largo plazo El objetivo de la empresa (SA) es maximizar el valor actual del flujo de beneficios. 1. Factores fijos: cosas que hay que pagar incluso si no produce nada (fábrica, maquinas,…) Es lo mismo que maximizar el valor actual de la empresa, o el valor en bolsa, que representa el valor actual de los dividendos pagados a los accionistas. 2. Factores variables: se puede utilizar en cantidades diferentes, sólo se paga lo que se utiliza (harina, huevos, mantequilla,…) Maximización del beneficio a corto plazo Rectas isobeneficio 1 bien, 1 factor variable ( x1), 1 factor fijo x 2 ≡ x~ 2 . La recta isobeneficio de $Π consiste de todas los planes de producción ( x1, ~ x2 , y) que generan un nível constante de beneficios $Π . Función de producción (corto plazo) Maximizar Solución ~ ). y = f ( x1 , x 2 ~ . Π = py − w 1x 1 − w 2 x 2 p PM1 ( x , ~ x2 ) = w1 * 1 Coste fijo 3. Factores cuasifijos: Se necesita en una cantidad fija en caso de producir algo, pero no se paga cuando no se produce nada (publicidad, electricidad,…) La ecuación de la recta isobeneficio es Es decir: ~ . Π ≡ py − w 1x1 − w 2 x 2 y= ~ Π + w 2x w1 2. x1 + p p Valor PM = precio 1 Rectas isobeneficio y B m io fic e en or ay Π ≡ Π′′ 19.01 Π ≡ Π ′′ Π ≡ Π′ Pendientes = + w1 p x1 Maximización del beneficio a largo plazo 19.02 1 bien, 2 factores variables ( Función de producción Maximizar Solución Maximización de beneficios y rendimientos de escala 1. Rendimientos constantes de escala implica beneficios zero (a largo plazo) 2. Rendimientos crecientos de escala no tiene sentido si el mercado es competitivo x1 , x 2 ), y= f (x1, x2). Π = py − w1x1 − w2 x2. p PM1 ( x1* , x2* ) = w1 p PM 2 ( x1* , x2* ) = w2 Rentabilidad revelada Si observamos en dos momentos distintos (t y s) dos elecciones (planes de producción) distintos, (pt, wt, yt, xt) y (ps, ws, ys, xs) y la empresa es maximizadora, entonces: ptyt - wtxt ≥ ptys - wtxs psys - wsxs ≥ psyt - wsxt 2 Rentabilidad revelada Es equivalente a ptyt - wtxt ≥ ptys - wtxs -psyt + wsxt ≥ -psys + wsxs Sumando las dos: (pt - ps)yt - (wt - ws)xt ≥ (pt - ps)ys - (wt - ws)xs Re-escribir: (pt - ps)(yt - ys) - (wt - ws)(xt - xs) ≥ 0 O ∆p∆y - ∆w∆x ≥ 0 Una manera rápida de hacer estática comparativa! 3