Teorema de Pitágoras

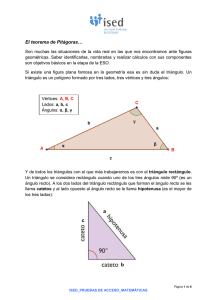
A. DEFINICIÓN TEOREMA DE PITÁGORAS
El Teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los dos catetos. Si un triángulo rectángulo tiene catetos de
longitudes a y b , y la medida de la hipotenusa es c , se establece que: a 2 b2 =c 2
Para calcular la hipotenusa, c, extraemos la raíz cuadrada a los dos miembros de la expresión anterior:
 c 2= a 2b 2  c= a 2b 2
.
Para calcular el cateto b, procederemos así:
a 2b 2=c 2  b 2=c 2− a 2  b=  c 2− a 2
Ejemplo 1: Calcula la hipotenusa de un triángulo rectángulo
de catetos a = 8 cm y b = 6 cm.
a=  826 2= 6436=  100=10 cm Se dice que 6, 8 y 10
forman una terna pitagórica.
Ejemplo 2: Calcula un cateto de un triángulo rectángulo, sabiendo que la hipotenusa mide 13 cm
y el otro cateto mide 5 cm.
a=  132−52= 169−25=  144=12 cm Se dice que 5, 12 y 13 forman una terna pitagórica.
B. DOS DEMOSTRACIONES GEOMÉTRICAS:
Comenzamos con dos cuadrados de lados a y b, respectivamente,
colocados lado a lado. La superficie total de los dos cuadrados es
a 2 b2 .
La construcción no se inició con un triángulo, pero ahora nos
acercamos a dos de ellos, tanto con los lados a y b y la hipotenusa
c.
Hay que tener en cuenta que el segmento común a los dos cuadrados se ha eliminado. En este punto tenemos, por tanto, dos triángulos y una forma de aspecto extraño.
Como último paso, giramos 90º los triángulos, cada uno en torno
a su vértice superior: El de la derecha se gira en sentido horario
mientras que el triángulo de la izquierda se gira en sentido antihorario.
Obviamente, la forma resultante es un cuadrado con el lado c de
área c 2 .
2
2
a b =c
2
Teorema de Pitágoras
Otra demostración sería:
Los cuadrados compuestos en el centro y a la derecha tienen áreas equivalentes. Quitándoles los
cuatro triángulos el teorema de Pitágoras queda demostrado.
b2
2
1
4
3
c2
1
2
a2
3
4
C. APLICACIÓN DEL TEOREMA DE PITÁGORAS
Ejemplo 3: Construye un hexágono de 3 cm de lado y calcula su área:
“l” es el radio de la circunferencia, que mide lo mismo
que el lado del hexágono.
“a” es la apotema del hexágono, que va desde el centro
al punto medio de un lado.
Fórmula del área de cualquier polígono regular:
A=
perímetro · apotema P · a
=
2
2
Perímetro=P =3· 6=18 cm
1º calculamos la apotema
Observa en el dibujo que la apotema,a, es un cateto de un triángulo cuya hipotenusa, l, mide 3
cm, y el otro cateto, c, mide 1,5 cm.
a= l 2−c 2= 32−1,52= 9−2,25= 6,75≃2,6 cm
2º Calculamos el área del hexágono:
A=
18 · 2,6
2
=23,4 cm
2
Teorema de Pitágoras