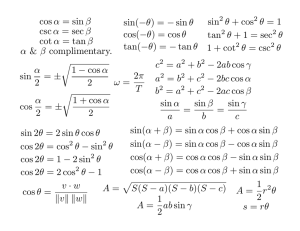Trigonometr´ıa plana - Universidad de Murcia

UNIVERSIDAD DE MURCIA
Óptica y Optometrı́a
Resúmenes
Curso 2004-2005
Departamento de Matemáticas
Trigonometrı́a plana
Relaciones entre razones trigonométricas:
tan α =
cos α
1
1
sen α
, cot α =
, csc α =
, sec α =
cos α
sen α
sen α
cos α
1
1
− 1 = sec2 α − 1, cot2 α =
− 1 = csc2 α − 1
2
cos α
sen2 α
Razones de ángulos suplementarios:
sen2 α + cos2 α = 1, tan2 α =
sen(π − α) = sen α, cos(π − α) = − cos α, tan(π − α) = − tan α
Razones de ángulos que difieren en π:
sen(π + α) = − sen α, cos(π + α) = − cos α, tan(π + α) = tan α
Razones de ángulos opuestos:
sen(−α) = − sen α, cos(−α) = cos α, tan(−α) = tan α
Razones de ángulos complementarios:
π
π
π
− α = cos α, cos
− α = sen α, tan
− α = cot α
sen
2
2
2
Suma y diferencia de ángulos:
sen(α ± β) = sen α cos β ± sen β cos α, cos(α ± β) = cos α cos β ∓ sen β sen α
tan(α ± β) =
tan α ± tan β
1 ∓ tan α tan β
Ángulo doble:
sen 2α = 2 sen α cos α, cos 2α = cos2 α − sen2 α, tan 2α =
2 tan α
1 − tan2 α
Ángulo mitad:
r
r
r
1 − cos α
α
1 + cos α
α
1 − cos α
α
, cos = ±
, tan = ±
sen = ±
2
2
2
2
2
1 + cos α
Transformaciones de sumas en productos:
α+β
α−β
α+β
α−β
cos
, sen α − sen β = 2 cos
sen
2
2
2
2
α+β
α−β
α+β
α−β
cos α + cos β = 2 cos
cos
, cos α − cos β = −2 sen
sen
2
2
2
2
α+β
tan 2
sen α + sen β
=
sen α − sen β
tan α−β
2
sen α + sen β = 2 sen
Dado un triángulo cualquiera, con la notación de la figura:
A
c
B
b
a
C
Teorema del coseno.- Se verifican las igualdades siguientes:
a2 = b2 + c2 − 2bc cos A, b2 = a2 + c2 − 2ac cos B, c2 = b2 + a2 − 2bc cos C
Teorema de los senos.- En todo triángulo cada lado en proporcional al seno de su ángulo
opuesto, es decir, se cumple:
a
b
c
=
=
sen A
sen B
sen C