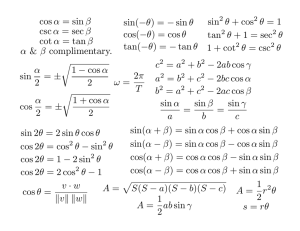Formulario de Trigonometr´ıa b ˆ C a ˆ B c A Razones principales sin
Anuncio

Formulario de Trigonometrı́a B̂ a c  b Ĉ Razones principales Razones inversas cateto opuesto c = hipotenusa a cateto contiguo b cos Ĉ = = hipotenusa a cateto opuesto c tan Ĉ = = cateto contiguo b hipotenusa a 1 = = cateto opuesto c sin Ĉ hipotenusa a 1 sec Ĉ = = = cateto contiguo b cos Ĉ cateto contiguo b 1 cot Ĉ = = = cateto opuesto c tan Ĉ sin Ĉ = csc Ĉ = Reducción del segundo al primer cuadrante sin(180 − α) = sin α cos(180 − α) = − cos α tan(180 − α) = − tan α sin(90 + α) = cos α cos(90 + α) = sin α tan(90 + α) = − cot α Reducción del tercero al primer cuadrante sin(270 − α) = − cos α cos(270 − α) = − sin α tan(270 − α) = cot α sin(180 + α) = − sin α cos(180 + α) = − cos α tan(180 + α) = tan α Reducción del cuarto al primer cuadrante sin(360 − α) = sin(−α) = − sin α cos(360 − α) = cos(−α) = cos α tan(360 − α) = tan(−α) = − tan α sin(270 + α) = − cos α cos(270 + α) = − sin α tan(270 + α) = cot α Ángulos suplementarios sin(90 − α) = cos α cos(90 − α) = sin α tan(90 − α) = cot α Reducción a la primera vuelta sin(360n + α) = sin α cos(360n + α) = cos α tan(360n + α) = tan α 1 Relaciones entre las razones trigonométricas Teorema de Pitágoras: sin2 α + cos2 α = 1. tan α = sin α cos α 1 + tan2 α = sec2 α 1 + cot2 α = csc2 α Fórmulas de la suma y resta de ángulos sin(α ± β) = sin α cos β ± cos α sin β cos(α ± β) = cos α cos β ∓ sin α sin β tan(α ± β) = tan α ± tan β 1 ∓ tan α tan β Fórmulas del ángulo doble Fórmulas del ángulo mitad sin(2α) = 2 sin α cos α sin cos(2α) = cos2 α − sin2 α α cos 2 tan α tan(2α) = 1 − tan2 α tan 2 α α 2 2 r 1 − cos α =± r 1 + 2cos α =± r 1 − 2cos α =± 1 + cos α Sumas y restas de senos y cosenos α+β α−β cos 2 2 α−β α+β sin α − sin β = 2 cos sin 2 2 α+β α−β cos 2 2 α−β α+β cos α − cos β = −2 sin sin 2 2 Teorema del seno Teorema del coseno sin α + sin β = 2 sin a sin  = b sin B̂ = cos α + cos β = 2 cos c a2 = b2 + c2 − 2bc cos  sin Ĉ o, equivalentemente b2 = a2 + c2 − 2ac cos B̂ sin  sin B̂ sin Ĉ = = a b c c2 = a2 + b2 − 2ab cos Ĉ 2