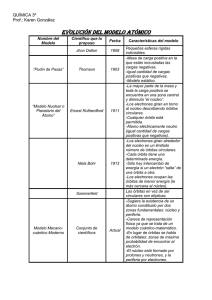
Max Plank determina que para la luz ΔE = h ν donde
Anuncio

Max Plank determina que para la luz ΔE = h ν donde ν es la frecuencia de la luz y h es la constante de Plank h = 6.62 10 -34 Js En 1913 Niels Bohr, desarrolló su modelo atómico de acuerdo a cuatro postulados fundamentales: 1. Los electrones orbitan el átomo en órbitas circulares a las que corresponden niveles discretos y cuantizados de energía. Por tanto, no todas las órbitas están permitidas, tan sólo un número finito de éstas. 2. Los electrones pueden saltar de un nivel electrónico a otro sin pasar por estados intermedios. 3. El salto de un electrón de un nivel cuántico a otro implica la emisión o absorción de un único cuanto de luz (fotón) cuya energía corresponde a la diferencia de energía entre ambas órbitas. 4. Las órbitas permitidas tienen valores discretos o cuantizados del momento angular orbital L de acuerdo con la siguiente ecuación: L = n h/2π Postulado 1: los electrones giran en órbitas estables alrededor del núcleo sin absorber o emitir energía radiante. Por tanto, la fuerza electromagnética actúa como centrípeta: F e= Keqq' r2 e2 F e =K e 2 r como q = carga del electrón e-, queda 2 La fuerza centrípeta será 2 Igualándolas: Ke m v e = e 2 r r F c= mv r donde m es la masa del electrón me 2 r= y despejando K e e2 mev2 Postulado 4: Sólo son posibles las órbitas en que el momento angular es múltiplo de h/2π Para órbitas circulares el momento angular L = r p = r mv Si debe ser múltiplo de h/2π y la masa de lo que gira es la masa del electrón, me, entonces: L = n h/2π y por tanto, L = r me v = n h/2π v =n Despejando v tenemos: r= Como el postulado 1 implica que 2 h ℏ v 2 =n 2 ℏ =n r 2 m e2 2 pi rm e rm e K e e2 mv 2 2 2 sustituimos v2 en esta expresión: K e e r me r= m e n 2 ℏ2 Cuando n=1, r = 0.0529 nm , el radio de Bohr 2 r =n 2 y despejando 2 ℏ =a n 2 2 K e e me Postulado 3: Al saltar de órbita, absorbe o emite energía según los quantos de Plank. ΔE = h ν Es decir, el incremento de energía será 1 e2 E =E c E p= m e v 2−K e 2 r Para un electrón, la energía total es 2 2 2 m v e e 2 K e 2= e m v = K e e r r r Pero en el postulado 1 hemos visto que luego y por tanto 1 e2 e2 e2 E = K e − K e =−K e 2 r r 2r y si sustituimos el radio del postulado 2: 2 ℏ r =n 2 =a n 2 K ee2 me tenemos que 2 2 4 e K e e me m e 1 e2 1 E =−K e =−K e =−K e 2 e 2 2 =−b 2 2 2 2r 2n ℏ 2ℏ n n Si un electrón salta ente dos órbitas de números cuánticos n1 y n2, la energía emitida o absorbida será: ΔE = E2 -E1 = −K e 2 m e e 4 2 ℏ2 K e2 m e e 4 1 1 1 1 − = 2 2 2 2− n2 n1 2ℏ n 1 n 22 = hν Este resultado coincidía con el que los espectroscopistas habían encontrado en los espectros del hidrógeno ya que, como para la luz su velocidad c es c= λ ν , podemos escribir: K e2 m e e 4 1 1 1 1 1/λ = ν/c = 2 2 − 2 =R 2− 2 ℏ c h n 1 n2 n 1 n 22 donde R es la constante de Rydberg