1 Comparación de varianzas, dos poblaciones nor
Anuncio

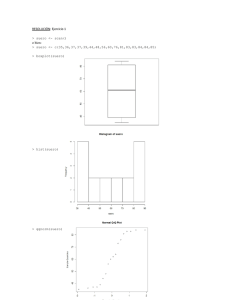
Inferencia Estadı́stica II Contrastes de hipótesis con R 1 Comparación de varianzas, dos poblaciones normales Se han hecho cuatro determinaciones quı́micas en dos laboratorios A y B con los resultados A: 26,24,28,27; B: 20 34 23 22. Se pide: • Comparar las varianzas de las dos muestras con nivel de significación 5%, encontrar la RR y el p-value > A<-c(26,24,28,27) > B<-c(20 ,34, 23 ,22) > var.test(A,B, alternative="two.sided") F test to compare two variances data: A and B F = 0.0737, num df = 3, denom df = 3, p-value = 0.05977 alternative hypothesis: true ratio of variances is not equal to 1 95 percent confidence interval: 0.004772546 1.137623965 sample estimates: ratio of variances 0.07368421 > var.test(A,B, alternative="less") F test to compare two variances data: A and B F = 0.0737, num df = 3, denom df = 3, p-value = 0.02988 alternative hypothesis: true ratio of variances is less than 1 95 percent confidence interval: 0.000000 0.683541 sample estimates: ratio of variances 0.07368421 1 > var.test(A,B, alternative="greater") F test to compare two variances data: A and B F = 0.0737, num df = 3, denom df = 3, p-value = 0.9701 alternative hypothesis: true ratio of variances is greater than 1 95 percent confidence interval: 0.007942995 Inf sample estimates: ratio of variances 0.07368421 • Comparar las varianzas de las dos muestras con nivel de significación 2%, encontrar la RR y el p-value > var.test(A,B, alternative="two.sided", coef.level=0.98) F test to compare two variances data: A and B F = 0.0737, num df = 3, denom df = 3, p-value = 0.05977 alternative hypothesis: true ratio of variances is not equal to 1 95 percent confidence interval: 0.004772546 1.137623965 sample estimates: ratio of variances 0.07368421 > #The Critical region is given by [0, 0.0339] union [29.4567] porque > qf(0.01, 3, 3, lower.tail=TRUE) [1] 0.03394814 > qf(0.01, 3, 3, lower.tail=FALSE) [1] 29.45670 > var.test(A,B, alternative="less", coef.level=0.98) 2 F test to compare two variances data: A and B F = 0.0737, num df = 3, denom df = 3, p-value = 0.02988 alternative hypothesis: true ratio of variances is less than 1 95 percent confidence interval: 0.000000 0.683541 sample estimates: ratio of variances 0.07368421 > #The Critical region is given by [0, 0.0552] > qf(0.02, 3, 3, lower.tail=TRUE) [1] 0.05521903 porque > var.test(A,B, alternative="greater", coef.level=0.98) F test to compare two variances data: A and B F = 0.0737, num df = 3, denom df = 3, p-value = 0.9701 alternative hypothesis: true ratio of variances is greater than 1 95 percent confidence interval: 0.007942995 Inf sample estimates: ratio of variances 0.07368421 > #The Critical region is given by [18.1097, Inf) > qf(0.02, 3, 3, lower.tail=FALSE) [1] 18.1097 3 porque 2 Comparación de medias de dos poblaciones con igual varianza Una compañia introduce un curso de mejora de las ventas para sus empleados. Se tomó una muestra aleatoria de 6 empleados y se grabaron los datos de ventas de estos empleados antes y después del curso. Empleado 1 2 3 4 5 6 Ventas antes del curso Ventas después del curso 12 18 18 24 25 24 9 14 14 19 18 21 Estudiar si hay suficiente evidencia para concluir que el curso fue un éxito al 5% de nivel de significación. Muestras independientes > x.B<-c(12 ,18 ,25,9,14,18) > x.A<-c(18,24,24,14,19,21) > ?t.test > mean(x.B) [1] 16 > mean(x.A) [1] 20 > t.test(x.A, x.B, alternative="g", mu=0, paired=FALSE, var.equal=TRUE) Two Sample t-test data: x.A and x.B t = 1.4384, df = 10, p-value = 0.09044 alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval: -1.040250 Inf sample estimates: mean of x mean of y 20 16 Muestras apareadas > t.test(x.A, x.B, alternative="g", mu=0, paired=TRUE, var.equal=TRUE) Paired t-test 4 data: x.A and x.B t = 3.6515, df = 5, p-value = 0.007363 alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval: 1.792625 Inf sample estimates: mean of the differences 4 3 Función cuantı́lica Experimentalmente se miden los tiempo de sedimentación de determinadas partı́culas coloreadas, flotando en un cierto lı́quido. Los tiempos observados, ya ordenados, fueron: 0.19, 0.78, 0.96, 1.31, 2.78, 3.16, 4.15, 4.67, 4.85, 6.5, 7.35, 8.01, 8.27, 12.06, 31.75, 32.52, 33.91, 36.71, 72.89. • Construir la función de distribución empı́rica. > x<-c(0.19, 0.78, 0.96, 1.31, 2.78, 3.16, 4.15, 4.67, 4.85, 6.5, 7.35, 8.01, 8.27, 12.06, 31.75, 32.52, 33.91, 36.71, 72.89) > summary.stepfun(Fn) Step function with continuity ’f’= 0 , 19 knots with summary Min. 1st Qu. Median Mean 3rd Qu. Max. 0.19 2.97 6.50 14.36 21.91 72.89 and 20 plateau levels (y) with summary Min. 1st Qu. Median Mean 3rd Qu. Max. 0.00 0.25 0.50 0.50 0.75 1.00 > summary(Fn) Empirical CDF: 19 unique values with summary Min. 1st Qu. Median Mean 3rd Qu. Max. 0.19 2.97 6.50 14.36 21.91 72.89 > postscript("ecdf.ps") > plot(Fn) > dev.off() 5 0.0 0.2 0.4 Fn(x) 0.6 0.8 1.0 ecdf(x) 0 20 40 60 80 x • Determinar los cuartiles de la distribución muestral. Funcion cuantı́lica empı́rica ## Default S3 method: quantile(x, probs = seq(0, 1, 0.25), na.rm = FALSE, names = TRUE, type = 7, ...) Por defecto type=7, que no es vlida para cuando buscamos el cuantil discreto... para esto necesitamos poner type=1 o type=2 o type=3 > quantile(x, prob=c(0.25,0.5, 0.75), type=1) 25% 50% 75% 2.78 6.50 31.75 Funcion cuantı́lica continua > quantile(x, prob=c(0.25,0.5, 25% 50% 75% 2.4125 5.6750 16.9825 > quantile(x, prob=c(0.25,0.5, 25% 50% 75% 2.8750 6.5000 26.8275 > quantile(x, prob=c(0.25,0.5, 25% 50% 75% 2.78 6.50 31.75 > quantile(x, prob=c(0.25,0.5, 25% 50% 75% 6 0.75), type=4) 0.75), type=5) 0.75), type=6) 0.75), type=7) 2.970 4 6.500 21.905 Contraste de χ2 de Pearson de bondad de ajuste Una compañia que hace tractores toma una muestra diaria de 4 tractores para una inspección de la calidad de su producto. El número de tractores que necesitaban algún ajuste se tomó durante 200 dı́as que dio como resultado la siguiente tabla. Contrastar si el model binomial con p = 0.1 es apropiado. N. necesitando ajustes/dı́a (xi ) 0 1 2 3 4 Total N. de dı́as (oi ) 102 78 19 1 0 200 pi = P (X = xi ) si X ∼Bin(4, 0.1) Frecuencia esperada (ei ) 0.6561 131.22 0.2916 58.32 0.0486 9.72 0.0036 0.72 0.0001 0.02 1 200 El problema es que las clases 3 y 4 tienen menos de 5 elementos cada una. Ası́ que las agrupamos con la clase 2 y la tabla queda N. necesitando ajustes/dı́a (xi ) 0 1 2, 3 y 4 Total N. de dı́as (oi ) 102 78 20 200 pi = P (X = xi ) si X ∼ Bin(4, 0.1) Frecuencia esperada (ei ) 0.6561 131.22 0.2916 58.32 0.0523 10.46 1 200 (oi −ei )2 ei 6.51 6.64 8.70 21.85 > o.i<-c(102,78,20) > p.i<-c(0.6561,0.2916 + ) > pbinom(2, 4, 0.1, lower.tail=FALSE) [1] 0.0037 > pbinom(1, 4, 0.1, lower.tail=FALSE) [1] 0.0523 > p.i<-c(0.6561,0.2916, 0.0523) > chisq.test(x=o.i, p=p.i) Chi-squared test for given probabilities data: o.i X-squared = 21.8486, df = 2, p-value = 1.802e-05 7 5 Contraste de Kolmogorov–Smirnov de bondad de ajuste Contrastar si la muestera siguiente de duraciones de vida puede suponerse exporencial: 16, 8, 10, 12, 6, 10, 20, 7, 2, 24 x Por lo tanto F (x) = 1 − e− x̄ donde x̄ = 11.50. Construimos una tabla con las discrepancias para cada valor de la muestra. David, el ks.test de R no parece funcionar bien. Para resolver el problema he hecho lo siguiente y el output no tiene sentido. Puedes hecharle un vistazo y ver si a encuentras la forma, gracias > x<-c(16, 8, 10,12,6,10,20,7,2,24) > y<-rexp(50, mean(x)) > ks.test(x,y) Two-sample Kolmogorov-Smirnov test data: x and y D = 1, p-value = 1.156e-07 alternative hypothesis: two-sided Warning message: cannot compute correct p-values with ties in: ks.test(x, y) > mean(x) [1] 11.5 > ks.test(x,"pexp", rate=mean(x)) One-sample Kolmogorov-Smirnov test data: x D = 1, p-value = 4.122e-09 alternative hypothesis: two-sided 6 Contrastes de normalidad > x<-c(20,22,24,30,31,32,38) > shapiro.test(x) 8 Shapiro-Wilk normality test data: x W = 0.9478, p-value = 0.7096 Esta muestra es pequeña, en general el test de Kolmogorov-Smirnov-Llliefords no es tan eficiente. Vamos a ver los resultados. > x<-c(20,22,24,30,31,32,38) > mean(x) [1] 28.14286 > var(x) [1] 40.80952 > sd(x) [1] 6.388233 > help.search("Kolmogorov-Smirnov") > ?ks.test > ks.test(x, "pnorm",mean=mean(x), sd=sd(x)) One-sample Kolmogorov-Smirnov test data: x D = 0.1858, p-value = 0.9345 alternative hypothesis: two-sided 9