Enunciados
Anuncio

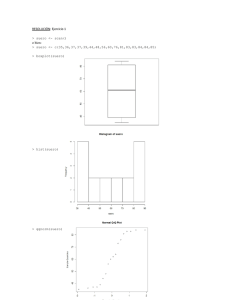
Examen final de ESTADÍSTICA APLICADA 16 de mayo de 2013 Primer Curso de Bioquı́mica APELLIDOS: NOMBRE: EXPLICAR DEBIDAMENTE LA RESOLUCIÓN DE CADA PROBLEMA 1. Interesada en el mecanismo de curación de las heridas, una bióloga tomó una colección de diez salamandras Notophtalmus viridescens. A todas ellas les amputó ambos cuartos traseros y en ellos hizo sendas pequeñas heridas cutáneas. Después mantuvo uno de los dos cuartos traseros en una solución que contenı́a benzamil y el otro cuarto en una solución de control. La investigadora pensaba que el benzamil perjudicarı́a la cicatrización. La tabla siguiente muestra la cantidad de cicatrización, expresada como el área (mm2 ) cubierta con nueva piel después de cuatro horas. Cuarto de Salamandra control (X) 1 0.55 2 0.15 3 0.00 4 0.13 5 0.26 6 0.07 7 0.20 8 0.16 9 0.03 10 0.42 Cuarto de benzamil (Y ) 0.14 0.08 0.00 0.13 0.10 0.08 0.11 0.00 0.05 0.21 a) (1 punto) A nivel α = 0.05, ¿hay suficiente evidencia a favor de la hipótesis de la investigadora? b) (0.5 puntos) Se introducen los datos en R: X = c(0.55, 0.15, 0, 0.13, 0.26, 0.07, 0.2, 0.16, 0.03, 0.42) Y = c(0.14, 0.08, 0, 0.13, 0.1, 0.08, 0.11, 0, 0.05, 0.21) Indica razonadamente cuál de los siguientes códigos serı́a el adecuado para resolver el problema planteado en (a). Interpreta los resultados del programa para el código elegido. Opción 1 > t.test(X,Y,alternative=’greater’) Welch Two Sample t-test data: X and Y t = 1.8344, df = 11.428, p-value = 0.04637 alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval: 0.00260478 Inf sample estimates: mean of x mean of y 0.197 0.090 1 Opción 2 > t.test(X,Y,alternative=’greater’,paired=TRUE) Paired t-test data: X and Y t = 2.5188, df = 9, p-value = 0.01642 alternative hypothesis: true difference in means is greater than 0 95 percent confidence interval: 0.02912925 Inf sample estimates: mean of the differences 0.107 Opción 3 > t.test(X,Y,paired=TRUE) Paired t-test data: X and Y t = 2.5188, df = 9, p-value = 0.03283 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: 0.01090343 0.20309657 sample estimates: mean of the differences 0.107 c) (1 punto) Determina la recta de regresión de Y sobre X, sabiendo que 10 X xi = 1.97 10 X i=1 i=1 10 X 10 X i=1 x2i = 0.6573 yi = 0.90 yi2 = 0.1180 i=1 10 X xi yi = 0.2492 . i=1 Dibújala (aproximadamente) sobre el diagrama de dispersión de los datos (Figura 1). Observación: Indica claramente cómo obtienes los parámetros de la recta a partir de medias, varianzas, etc. No se considera válido obtenerlos directamente mediante la función de regresión de la calculadora. d) (0.5 puntos) Determina el coeficiente de correlación r entre X e Y . Interpreta el valor obtenido de r, ası́ como el valor de la pendiente b de la recta de regresión. ¿Te parece que apoyan la hipótesis de la investigadora? 2 0.20 0.15 0.00 0.05 Y 0.10 0.0 0.1 0.2 0.3 X 0.4 0.5 Figura 1: Diagrama de dispersión de los datos del Problema 1 2. Se han llevado a cabo varios estudios para analizar la relación entre someterse a una vasectomı́a y padecer cáncer de próstata. En un trabajo de Giovanucci et al. (1993) aparecen los siguientes resultados: de 21300 hombres que no se habı́an hecho una vasectomı́a, 69 habı́an tenido cáncer de próstata, mientras que de 22000 hombres que se habı́a sometido a una vasectomı́a, 113 habı́an padecido posteriormente dicho tipo de cáncer. a) (1 punto) A un nivel de significación 0.01, ¿hay suficiente evidencia estadı́stica para afirmar que hacerse una vasectomı́a aumenta el riesgo de padecer cáncer de próstata? b) (0.5 puntos) Se realiza un análisis de los datos del enunciado con el programa R, obteniéndose: > prop.test(c(69,113),c(21300,22000),p=NULL,alternative="less",conf.level =0.99,correct=FALSE) 2-sample test for equality of proportions without continuity correction data: c(69, 113) out of c(21300, 22000) X-squared = 9.3038, df = 1, p-value = 0.001143 alternative hypothesis: less 99 percent confidence interval: -1.0000000000 -0.0004555946 sample estimates: prop 1 prop 2 0.003239437 0.005136364 Indica qué tipo de análisis estadı́stico se ha realizado e interpreta los resultados. 3 3. Un cruce dihı́brido entre una lı́nea pura de guisantes altos con semillas lisas y una planta de guisante enana con semillas rugosas produce, en la segunda generación, una planta que tiene probabilidad 9/16 de ser alta y lisa. a) (0.7 puntos) Si se toma una muestra de 5 descendientes de la segunda generación, ¿qué probabilidad hay de que salgan exactamente cuatro plantas altas y lisas? ¿y de que salgan como mucho cuatro? b) (0.8 puntos) Si se toma una muestra de cien descendientes, ¿cuál es la probabilidad de que al menos 60 de ellos sean plantas altas y lisas? 4