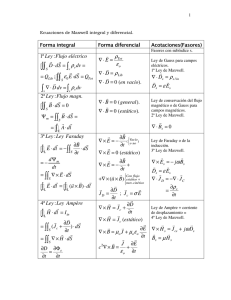
Ecuaciones de Maxwell en Forma Diferencial
Anuncio

Ecuaciones de Maxwell en Forma Diferencial 1 ECUACIONES DE MAXWELL: FORMA INTEGRAL Las ecuaciones de Maxwell son las leyes fundamentales para describir el comportamiento de los campos eléctricos y magnéticos. En el cuadro siguiente aparecen estas ecuaciones cuyos nombres son: Gauss para el campo eléctrico, Faraday, Gauss para el campo magnético y AmpèreMaxwell qenc E dS 0 d B E E dl dt B dS 0 d B dl 0 I 0 dt E 2 Teoremas de Gauss y Stokes Para transformar estas ecuaciones a la forma diferencial, aplicaremos los teoremas integrales de Gauss y Stokes dV G d S G Gx G y Gz donde G es la divergenci a de G x y z G d l x G d S iˆ donde xG x ˆj kˆ y z Gx Gy Gz es el rotacional de G, siendo i xi 3 Ecuaciones de Maxwell: Forma Diferencial Aplicando el Teorema de Gauss, podemos expresar las leyes de Gauss para E y B en forma diferencial 1 E d S E dV E 0 dV 0 0 dV E 0 B dS B dV 0 B 0 4 Ecuaciones de Maxwell: Forma Diferencial (II) De la misma manera, aplicando el Teorema de Stokes, podemos expresar las leyes de Faraday y Ampére-Maxwell en forma diferencial d B E dl xE dS dt B dS t dS B B xE t dS 0 xE t d B dl xB dS 0 J dS 0 0 dt E dS E E x B J d S 0 x B J 0 0 0 0 0 0 t t 5