Tema 1.- Correlación Lineal

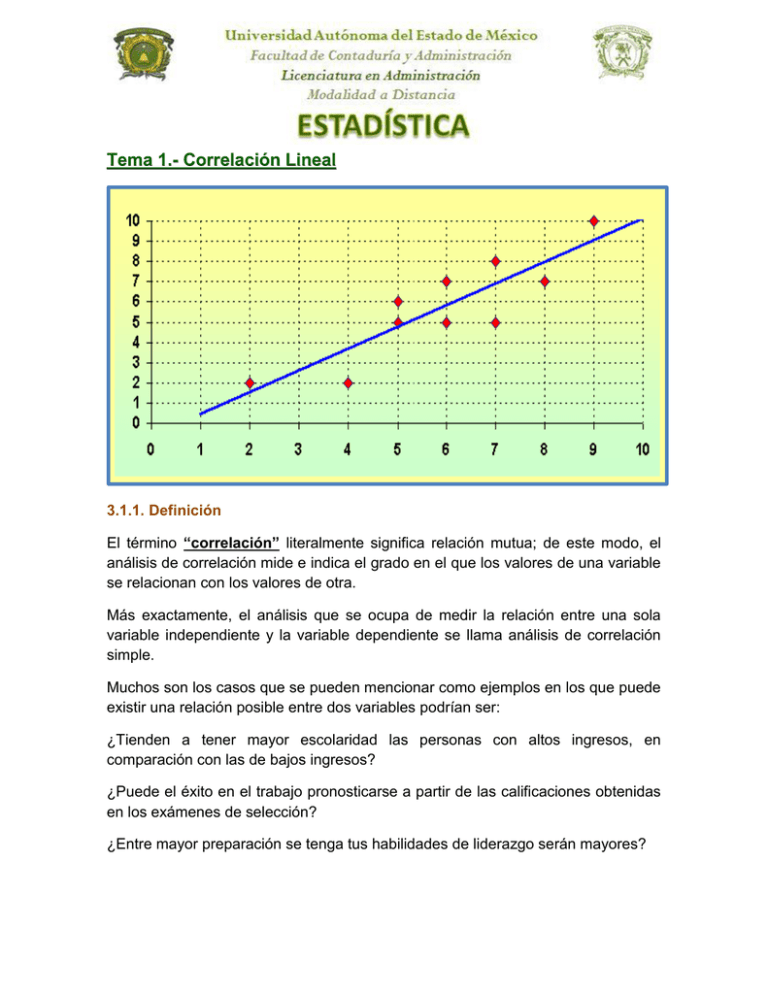
Tema 1.- Correlación Lineal
3.1.1. Definición
El término “correlación” literalmente significa relación mutua; de este modo, el
análisis de correlación mide e indica el grado en el que los valores de una variable
se relacionan con los valores de otra.
Más exactamente, el análisis que se ocupa de medir la relación entre una sola
variable independiente y la variable dependiente se llama análisis de correlación
simple.
Muchos son los casos que se pueden mencionar como ejemplos en los que puede
existir una relación posible entre dos variables podrían ser:
¿Tienden a tener mayor escolaridad las personas con altos ingresos, en
comparación con las de bajos ingresos?
¿Puede el éxito en el trabajo pronosticarse a partir de las calificaciones obtenidas
en los exámenes de selección?
¿Entre mayor preparación se tenga tus habilidades de liderazgo serán mayores?
Estos y problemas semejantes se prestan a un análisis de correlación. El resultado
de un análisis de este tipo es un coeficiente de correlación, valor que cuantifica
el grado de correlación.
Ahora dicho análisis de correlación parte de la base del estudio que podemos
hacer de dos variables estadísticas y que se denomina Distribución Bidimensional:
DISTRIBUCIONES BIDIMENSIONALES
Cuando sobre una población estudiamos
simultáneamente los valores de dos variables
estadísticas, el conjunto de los pares de valores
correspondientes a cada individuo se denomina
distribución bidimensional.
NUBE DE PUNTOS O DIAGRAMA DE DISPERSIÓN
La primera forma de describir una distribución
bidimensional es representar los pares de valores en el
plano cartesiano. El gráfico obtenido recibe el nombre de
nube de puntos o diagrama de dispersión
RECTA DE REGRESIÓN.
Cuando observamos una nube de puntos podemos apreciar si
los puntos se agrupan cerca de alguna curva. Aquí nos
limitaremos a ver si los puntos se distribuyen alrededor de
una recta. Si así ocurre diremos que hay correlación lineal.
La recta se denomina Recta de regresión.
En este caso podemos observar que empíricamente podemos saber sí existe o no
una correlación entre dos variables estadísticas, como Licenciado en
Administración en ocasiones el análisis de los datos tendrá que pasar por
comparar uno con otro para saber si existe dicha correlación por ejemplo
determinar cual de los gastos que tiene una empresa es que mayor influencia
tiene sobre las utilidades; o si el horario en que labora un trabajador depende de la
productividad en una planta ensambladora. Sin embargo aunque observando la
gráfica podemos definir cierto comportamiento; no sabremos a ciencia cierta si
esta correlación es fuerte, débil o nula; o dar un dato cuantitativo sobre ella.
Este grado o intensidad de relación entre dos variables continuas, se resume
mediante un coeficiente de correlación que se conoce como “r de Pearson” en
honor del matemático Karl Pearson (el mismo del coeficiente que mide la
asimetría). Dicha técnica es válida solamente si es posible establecer los
siguientes supuestos:
•
La relación entre las dos variables es lineal
•
Ambas variables son variables aleatorias
•
Los valores observados (muestreados) de cada variable
independientes de los demás valores observados de esa variable
•
Las distribuciones condicionales de cada variable, dados los
diferentes valores de la otra variable, son distribuciones normales.
son
3.1.2. Fórmula
Para calcular el coeficiente de Pearson se usa la siguiente fórmula:
3.1.3. Interpretación
El coeficiente de correlación así calculado presenta dos propiedades que
establecen la naturaleza de la relación entre dos variables, estas son
•
Su signo (+ ó – ), este es igual al de la pendiente de una recta que podría
“ajustarse” a los datos si éstos se graficaran en el llamado diagrama de dispersión
y que se muestra en el ejemplo más adelante
•
Su magnitud, ésta indica qué tan cerca están de la “recta” los puntos que en
el diagrama de dispersión resultan de graficar los valores de las dos variables
analizadas.
Por ejemplo, los valores próximos a -1.00 ó +1.00 indican que los valores están
bastante cerca de la recta o sobre ella, mientras que los valores próximos a 0
sugieren mayor dispersión dando lugar a la siguiente interpretación:
O de otra forma:
Ejemplo Cálculo de Coeficiente de Correlación de Pearson
Has sido nombrado Jefe del Departamento de Ventas de una compañía que
manufactura dispositivos electrónicos automotrices para el mercado mexicano.
Una de tus estrategias para lograr el aumento en la colocación de pedidos por
parte de tus clientes es el contacto telefónico con ellos.
Para fundamentar tu estrategia has decidido hacer notar a tus superiores la
importancia de hacer llamadas extras cada día. En tal virtud, has reunido cierta
información acerca de la relación entre el número de llamadas y el número de
productos vendidos, estos datos se muestran en la tabla siguiente:
¿Qué comentarios puedes hacer respecto a la relación entre el número de
llamadas y la cantidad de productos vendidas?
Solución:
Paso 1. Construir Diagrama de Dispersión
Se denomina diagrama de dispersión o nube de puntos a la
representación, en un sistema de ejes cartesianos (X, Y), de
los valores observados de las variables, en el que a cada par
(xi,yj) se le asocia su frecuencia conjunta de observación nij.
Un diagrama de dispersión ofrece una idea bastante aproximada
sobre el tipo de relación existente entre dos variables. Pero, además,
un diagrama de dispersión también puede utilizarse como una forma
de cuantificar el grado de relación lineal existente entre dos
variables: basta con observar el grado en el que la nube de puntos se
ajusta a una línea recta.
Paso 2. Construir cuadro para cálculos:
Paso 3. Sustituir valores en la fórmula:
Paso 4. Interpretar el resultado:
El signo positivo indica que hay una relación directa entre el número de llamadas a
clientes y la cantidad de productos vendidos. El valor 0.759 está bastante
cercano a 1.00, por lo que se concluye que la relación es fuerte.
Dicho de otra forma, un aumento de 25% en las llamadas posiblemente
representaría un aumento de 25% en las ventas.
Como se puede apreciar el coeficiente de correlación no tiene unidades y su
interpretación queda en términos de fuerte, media o débil relación, lo cual puede
no ser suficiente; para completar la interpretación existe el llamado:
Coeficiente de determinación, este se obtiene elevando al cuadrado a r, y se
interpreta como proporción o porcentaje de variación de la variable
dependiente que se explica por la variación en la variable independiente.
Es decir:
Para el ejemplo anterior, este coeficiente de determinación resultaría r2 = (0.759)2
= 0.576 que se interpretaría como sigue: 57.6% de la variación en el número de
artículos vendidos se explica por la variación en el número de llamadas.
Actividad Preliminar 1: (Recuerda que estas actividades son opcionales y será
tu asesor quien defina aquellos que serán evaluados en tu curso. Sin embargo te
recomiendo que las realices para verificar efectivamente el nivel de aprendizaje
logrado)
Resuelve los siguientes problemas:
COEFICIENTE DE CORRELACIÓN Y DE DETERMINACIÓN
No.
1
Problema
Se desea saber si el aprovechamiento escolar de nivel universitario está relacionado
con el aprovechamiento respectivo a nivel de bachillerato. Parecería razonable esperar
que los alumnos tiendan a obtener aproximadamente las mismas calificaciones en la
universidad que en la preparatoria. Para medir esto, supón que cuentas con la
información que se muestra en la tabla siguiente:
ESTUDIANTE
CALIFICACIÓN EN CALIFICACIÓN
PREPARATORIA
EN UNIVERSIDAD
1
2
3
4
5
6
7
8
9
10
11
12
a)
b)
c)
d)
8.7
2.1
8.8
1.7
8.2
1.0
9.8
4.0
9.1
2.7
8.0
1.0
9.1
2.4
8.8
2.0
9.1
2.4
9.6
3.6
9.4
3.9
9.2
3.0
Cuál es la variable independiente y cuál la dependiente
Construir diagrama de dispersión
Calcular coeficiente de correlación e interpretar resultado
Calcular coeficiente de determinación e interpretar resultado
2
En un empleo que consiste en conectar componentes electrónicos en miniatura, se
tomó una muestra de 12 trabajadores a los cuales se les preguntó la experiencia que en
semanas tienen realizando dicho trabajo así como el número de componentes que les
fueron rechazados en su última jornada de trabajo. Tales datos se presentan en la
siguiente tabla:
Obrero
1
muestreado
Semanas
de 7
experiencia
Número
de 2
rechazos
6
a)
b)
c)
d)
2
3
4
5
6
7
8
9
10
11
12
9
6
14
8
12
10
4
2
11
1
8
2
0
28
16
23
18
24
26
38
22
32
25
Cuál es la variable independiente y cuál la dependiente
Construir diagrama de dispersión
Calcular coeficiente de correlación e interpretar resultado
Calcular coeficiente de determinación e interpretar resultado