7. Posición relativa parábola-recta
Anuncio
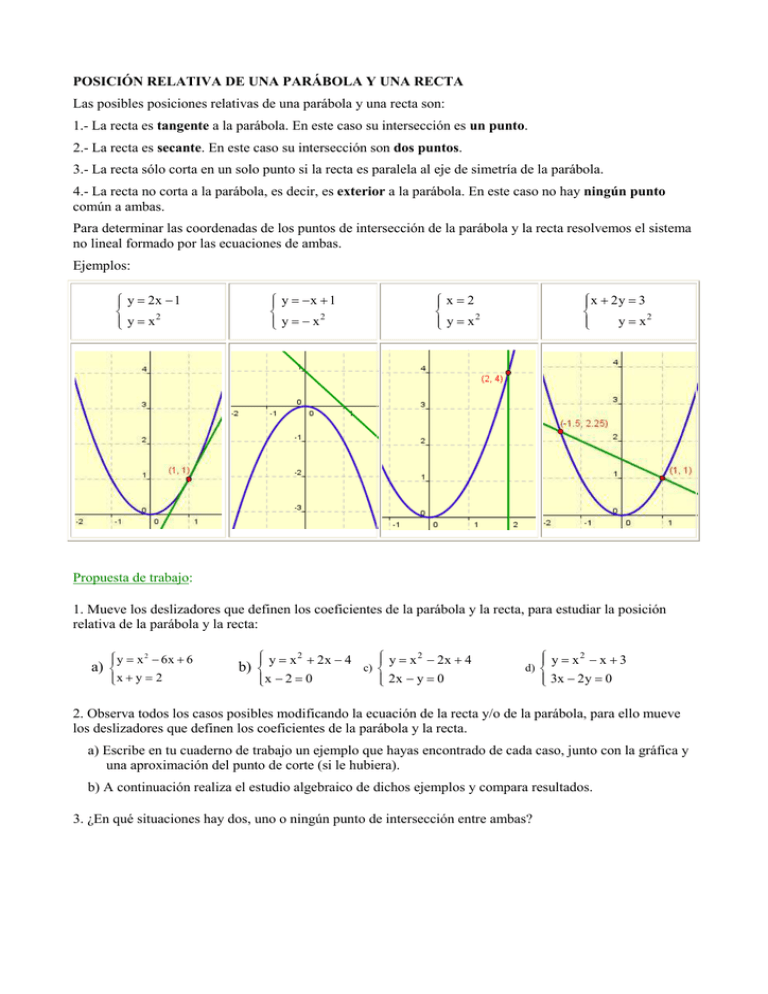
POSICIÓN RELATIVA DE UNA PARÁBOLA Y UNA RECTA Las posibles posiciones relativas de una parábola y una recta son: 1.- La recta es tangente a la parábola. En este caso su intersección es un punto. 2.- La recta es secante. En este caso su intersección son dos puntos. 3.- La recta sólo corta en un solo punto si la recta es paralela al eje de simetría de la parábola. 4.- La recta no corta a la parábola, es decir, es exterior a la parábola. En este caso no hay ningún punto común a ambas. Para determinar las coordenadas de los puntos de intersección de la parábola y la recta resolvemos el sistema no lineal formado por las ecuaciones de ambas. Ejemplos: y = 2x − 1 2 y = x y = − x + 1 2 y = − x x = 2 2 y = x x + 2y = 3 y = x2 Propuesta de trabajo: 1. Mueve los deslizadores que definen los coeficientes de la parábola y la recta, para estudiar la posición relativa de la parábola y la recta: y = x 2 − 6x + 6 a) x + y = 2 y = x 2 + 2x − 4 y = x 2 − 2x + 4 c) x − 2 = 0 2x − y = 0 b) y = x 2 − x + 3 3x − 2y = 0 d) 2. Observa todos los casos posibles modificando la ecuación de la recta y/o de la parábola, para ello mueve los deslizadores que definen los coeficientes de la parábola y la recta. a) Escribe en tu cuaderno de trabajo un ejemplo que hayas encontrado de cada caso, junto con la gráfica y una aproximación del punto de corte (si le hubiera). b) A continuación realiza el estudio algebraico de dichos ejemplos y compara resultados. 3. ¿En qué situaciones hay dos, uno o ningún punto de intersección entre ambas?


