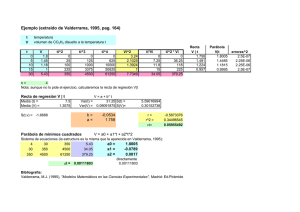
Consideremos la parabola de ecuacion y = x2. Calcular el punto B
Anuncio

Consideremos la parábola de ecuación y = x2. Calcula el punto B de esta parábola que está más cerca del punto A = (3, 0). Comprueba después que la recta BA es perpendicular a la tangente a la parábola en el punto B. SOLUCIÓN: - Lo que se nos pide es buscar el punto de la parábola en que la distancia a (3, 0) sea mínima. El punto B(x, y) al ser de la parábola y = x2, se puede escribir B(x, x2); que de esta forma se expresa con una sola incógnita. La función a minimizar es la distancia entre puntos: d(A, B) = x - 32 x2 0 = x4 x2 6x + 9 Como la raíz será mínima cuando el radicando sea mínimo, podemos minimizar: d2(A, B) = x4 + x2 - 6x + 9. Para hacerlo buscamos los ceros de su derivada. (d2(A, B))’ = 4x3 + 2x - 6. Como la suma de coeficientes es 0, el 1 será una raíz; descomponiendo por Ruffini: (d2(A, B))’ = (x - 1)(4x2 + 4x + 6) que sólo se anula en x = 1. Conociendo el signo de la derivada segunda en x = 1 podremos saber si se trata de un mínimo: (d2(A, B))’’ = 12x2 + 2, siempre positiva, por lo que en x = 1, la función es cóncava. Se tiene un mínimo en B(1, 1). - Dos rectas son perpendiculares cuando el producto de sus pendientes es -1. Un vector director de la recta AB es = (-2, 1), y la pendiente de la recta, la segunda componente dividida por la primera: m1 = - 1 . 2 Para calcular la pendiente de la recta tangente a la gráfica de la función y = x 2 en el punto B(1, 1), calcularemos la derivada en x = 1. f’(x) = 2x. f’(1) = 2, m2 = 2. m1m2 = - 1 2 = -1, por lo que las dos rectas son perpendiculares. 2