PANDEO El pandeo es un fenómeno de no linealidad geométrica
Anuncio
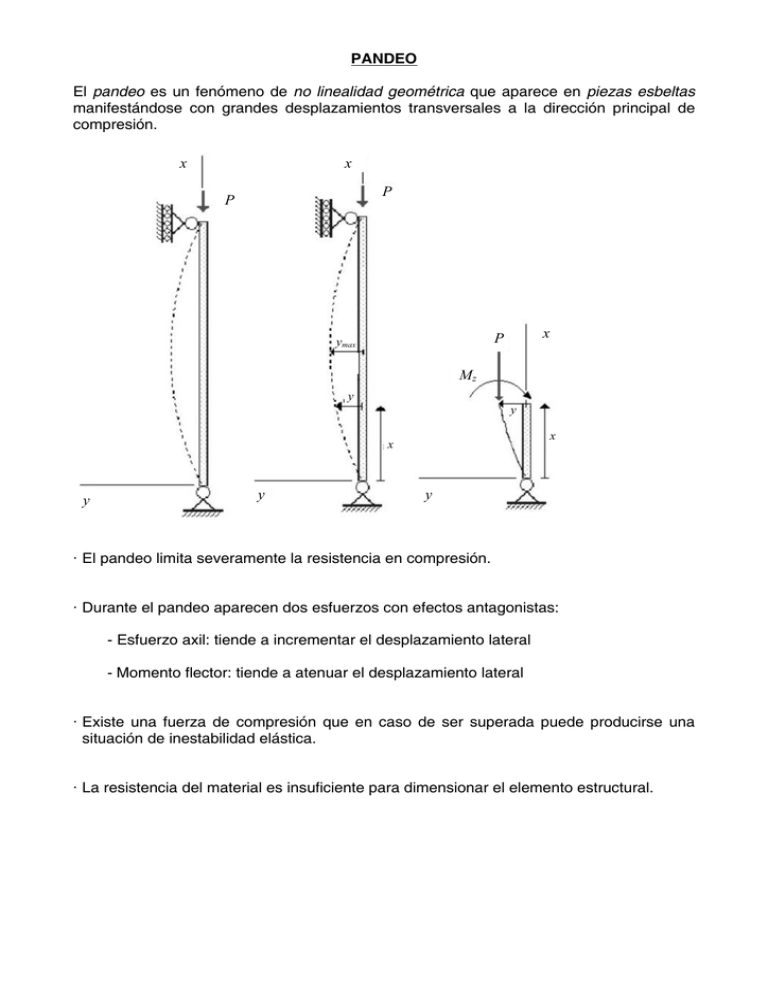
PANDEO El pandeo es un fenómeno de no linealidad geométrica que aparece en piezas esbeltas manifestándose con grandes desplazamientos transversales a la dirección principal de compresión. x x P P x P ymax Mz y y x x y y y · El pandeo limita severamente la resistencia en compresión. · Durante el pandeo aparecen dos esfuerzos con efectos antagonistas: - Esfuerzo axil: tiende a incrementar el desplazamiento lateral - Momento flector: tiende a atenuar el desplazamiento lateral · Existe una fuerza de compresión que en caso de ser superada puede producirse una situación de inestabilidad elástica. · La resistencia del material es insuficiente para dimensionar el elemento estructural. Barra esbelta doblemente articulada. Carga crítica de Euler. x P Mz y x y M z = − P y = EI z d2y dx 2 d2y P + y=0 2 EI z dx ⎛ ⎛ ⎞ P ⎞⎟ ⎜x P ⎟ y = C1 sin ⎜⎜ x cos C + 2 ⎟ ⎜ EI ⎟ z ⎠ ⎝ EI z ⎠ ⎝ Condiciones de contorno: x=0→ y=0 x=l → y=0 ⇒ C2 = 0 ⇒ ⎛ P ⎞⎟ C1 sin ⎜⎜ l ⎟=0 ⎝ EI z ⎠ ⎧• C1 = 0 ⎪ ⎛ ⇒⎨ P ⎜ ⎪• sin ⎜ l EI z ⎝ ⎩ ⎞ ⎟ = 0 ⇒ l P = nπ ⎟ EI z ⎠ P=n 2 π 2 EI z l2 (n = 1,2,...) (n = 1,2,...) La carga más pequeña corresponde a n = 1 Pcr = π 2 EI z l2 Carga Crítica de Euler OBS: La carga crítica de Euler no depende del límite de proporcionalidad σp del material. Deformada por pandeo Ecuación diferencial de la elástica: 1 ω= αz ρ = d2y ds 2 ⎡ ⎛ dy ⎞ 2 ⎤ ⎢1 + ⎜ ⎟ ⎥ ⎢⎣ ⎝ ds ⎠ ⎥⎦ 32 = Mz Py =− EI z EI z Si las deformaciones son pequeñas: αz αz d2y ds 2 ⎡ ⎛ dy ⎞ 2 ⎤ ⎢1 + ⎜ ⎟ ⎥ ⎢⎣ ⎝ ds ⎠ ⎥⎦ 32 d2y ≈ 2 ds ⇒ Py d2y =− 2 EI z ds Esta ecuación corresponde a la empleada en la determinación de la carga crítica de Euler. Volviendo a la ecuación diferencial de la elástica: ω= 1 ρ = dα z M z Py = =− ds EI z EI z dα z P y + =0 ds EI z d 2α z P dy + =0 2 EI z ds ds d 2α z P + sin α z = 0 2 EI z ds La flecha máxima se obtiene en el punto medio: l α z =0 y max = f = ∫ 2 dy = ∫ 0 α z = α z0 P Pcr f l 0º 20º 40º 60º ≤ 1 1.015 1.064 1.152 0 0.11 0.211 0.296 α z =α z 0 sin α z ds Longitud de pandeo Supóngase barras esbeltas sometidas a compresión con distintos tipos de enlace: · Se define la Longitud de Pandeo L como: L=βl l : longitud de la barra β : Coef. función del tipo de enlace · Carga crítica de Euler: Pcr = π 2 EI z L2 Tensión crítica de Euler. Esbeltez mecánica σ cr = iz : Radio de giro i z = Pcr π 2 EI z π 2 Ei z2 S π 2E π 2E = = = = 2 2 S λ SL2 SL2 ⎛L⎞ ⎜⎜ ⎟⎟ ⎝ iz ⎠ Iz S λ : Esbeltez mecánica L iz λ= σcr : Tensión crítica de Euler σ cr = π 2E λ2 Dominio de aplicación de la fórmula de Euler Hipérbola de Euler Validez de tensión crítica de Euler: π 2E σ cr = 2 ≤ σ p λ OBS.: · Piezas de esbeltez muy elevada · Piezas de esbeltez muy pequeña ⇒ λ ≥ λL = π 2E σp ⇒ La tensión crítica es muy pequeña ⇒ La tensión crítica de Euler carece de sentido Pandeo en el dominio anelástico ( λ < λ L ) Engensser-Shanley Tensiones superiores al límite elástico σ e el módulo de elasticidad tangente disminuye σ Módulo elástico tangente ET = dσ = tan β dε ε σ cr = π 2 ET λ2 Formula de Tetmajer Es una fórmula empírica σ cr = a − bλ + cλ2 E Acero dulce Fundición Madera de pino σe [kg/cm2] [kg/cm2] 106 1620 2.1·106 0.1·106 1900 99 λL a b c 105 3100 11.4 0 80 7760 120 0.53 100 293 1.94 0 Coeficiente de seguridad a pandeo γp Imperfecciones: las cargas descentradas y piezas con ligera curvatura inicial ⇓ Se aplica un coeficiente de seguridad que aumenta con la esbeltez (σ adm ) p = σ cr γp Método de los coeficientes ω de cálculo del pandeo ω= σ adm (σ adm ) p ⇒ ω = f (λ ) donde ya se ha tenido en cuenta (σ adm ) p = σ= σ cr γp & σ adm = σ P ≤ (σ adm ) p = adm S ω Tres planteamientos: σω = λ 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250 P ω ≤ σ adm S 0 1.01 1.03 1.07 1.12 1.19 1.30 1.45 1.65 1.89 2.18 2.50 2.86 3.25 3.68 4.14 4.63 5.15 5.70 6.28 6.90 7.54 8.22 8.92 9.66 1 1.02 1.04 1.07 1.12 1.20 1.31 1.47 1.67 1.92 2.21 2.53 2.90 3.29 3.72 4.18 4.68 5.20 5.76 6.34 6.96 7.61 8.29 8.99 S≥ P σ adm ω Coeficientes ω para aceros St 33 y St 37 2 3 4 5 6 7 1.02 1.02 1.02 1.02 1.02 1.03 1.04 1.04 1.04 1.05 1.05 1.06 1.08 1.08 1.08 1.09 1.09 1.10 1.13 1.14 1.14 1.15 1.16 1.17 1.21 1.22 1.23 1.24 1.25 1.26 1.33 1.34 1.36 1.37 1.39 1.40 1.49 1.51 1.53 1.55 1.57 1.59 1.70 1.72 1.74 1.77 1.79 1.82 1.95 1.97 2.00 2.03 2.06 2.09 2.24 2.27 2.30 2.33 2.37 2.40 2.57 2.60 2.64 2.68 2.71 2.75 2.94 2.97 3.01 3.05 3.09 3.13 3.33 3.38 3.42 3.46 3.50 3.55 3.77 3.81 3.86 3.90 3.95 4.00 4.23 4.28 4.33 4.38 4.43 4.48 4.73 4.78 4.83 4.88 4.94 4.99 5.26 5.31 5.36 5.42 5.48 5.53 5.81 5.87 5.93 5.99 6.05 6.11 6.40 6.46 6.53 6.59 6.65 6.71 7.03 7.09 7.15 7.22 7.28 7.35 7.67 7.74 7.81 7.88 7.94 8.01 8.36 8.43 8.49 8.57 8.64 8.71 9.07 9.14 9.21 9.29 9.36 9.43 P≤ 8 1.03 1.06 1.10 1.17 1.28 1.42 1.61 1.84 2.12 2.43 2.78 3.17 3.59 4.04 4.53 5.04 5.59 6.16 6.77 7.41 8.08 8.78 9.51 S σ adm 9 1.03 1.06 1.11 1.18 1.29 1.44 1.63 1.87 2.15 2.47 2.82 3.21 3.63 4.09 4.58 5.09 5.64 6.22 6.84 7.48 8.15 8.85 9.58 ω λ 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 σe γ








