masa y densidad
Anuncio

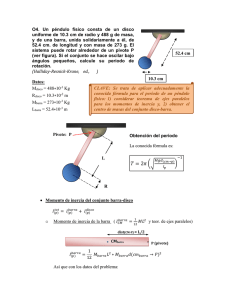
1 2 Introducción a la Física Paralelos 10 y 13. Profesor RodrigoVergara R MASA Y DENSIDAD Introducción a la Física Paralelos 10 y 13. Profesor RodrigoVergara R • Si v1 = v2, entonces M1 = M2. • Si v1 > v2, entonces M1 < M2 • Si v1 = 2·v2, entonces M1 = M2/2 • Si v1 < v2, entonces M1 > M2. • Si v1 = v2/2, entonces M1 =2·M2 En general, se puede demostrar que 1) Masa • Definir operacionalmente masa. • Indicar y utilizar unidades de masa: kg, lb, ton. • Conocer y describir prácticos para medir masas: balanzas y pesas. Masa e inercia M1 v 2 = ⇒ M1 ⋅ v 1 = M 2 ⋅ v 2 M 2 v1 Piense en las siguientes situaciones: • • Si camina con un vaso de agua en la mano y se detiene bruscamente, derrama agua. Si viaja en un bus concentrado en la lectura de un libro y el chofer frena bruscamente, resultará lanzado hacia delante. En ambas situaciones, se aprecia que los cuerpos oponen resistencia a los cambios en su estado de movimiento. Ese hecho se denomina INERCIA. El primer principio de Newton se refiere a ella. La expresión cuantitativa de la inercia se denomina MASA. En el lenguaje diario se suelen usar las palabras “masa” y “peso” como sinónimos. Por ejemplo, cuando uno va a la feria a comprar papas y pide que “le pesen un kilo de papas”, o cuando uno se sube a una balanza y dice “peso 80 kilos”. Sin embargo, masa y peso son cantidades físicas conceptualmente diferentes, aunque relacionadas. En el capítulo de fuerzas se tratará este asunto en detalle. Definición operacional de masa Unidades de masa. En el sistema MKS la unidad patrón de masa es el kilogramo o [kg], cuya definición operacional es la siguiente: “Un kilogramo es la masa de un cilindro particular de una aleación de platino e iridio sancionado por la 1º Conferencia General de Pesos y Medidas, celebrada en Paris en 1889, y que se encuentra depositado en la Oficina Internacional de Pesos y Medidas, en Sevres, Francia.” Además, 1 [kg] corresponde a la masa de 1 [litro] de agua en estado líquido. La medición de masas de cuerpos como automóviles, buques o containers se suele hacer en toneladas o [tons] En el sistema CGS la unidad patrón de masa es el gramo o [g]. Para definir operacionalmente el concepto de masa, vamos a considerar un fenómeno físico similar al siguiente: “Dos hombres están sobre patines idénticos. Los patines pueden rodar sin ningún impedimento sobre una superficie horizontal muy lisa. Los hombres se colocan frente a frente con las palmas de sus manos juntas y se empujan mutuamente. Si observamos que después de separarse, ellos retroceden con distinta rapidez, diremos que el que lo hace con menor rapidez tiene mayor masa” Este resultado va a ser posteriormente demostrado usando dinámica (FIS 100 y FIS 110) y Moméntum Lineal (FIS 110) cuerda M1 En el sistema británico, la unidad patrón de masa es la libra o [lb] M2 v1 v2 M1 M2 Figura 1) Definición operacional de masa Consideremos la siguiente situación, ilustrada en la figura 1. Dos cuerpos de masa total (considerando las ruedas) M1 y M2 comprimen un resorte y están sujetas por una cuerda. En cierto instante se corta la cuerda, y ambas masa salen disparadas en direcciones opuestas, con velocidades de magnitud v1 y v2, respectivamente. A través de diversas observaciones y mediciones se puede establecer que: 1[Kg ] ≅ 10 3 [g ] 1[ton ] ≅ 10 3 [Kg ] 1[lb] ≅ 453,59237 [g ] ≅ 0.454 [kg ] Medición de masas Existen tres instrumentos típicos para medir masas: las balanzas, las romanas y las básculas. Las balanzas se utilizan para pesar masas pequeñas de solo unos kilos de peso y a nivel de laboratorio. Éstas consisten en dos platos unidos por una viga pivoteada en su centro. Masas patrón Figura 2) Balanza para medir masas 3 4 Introducción a la Física Paralelos 10 y 13. Profesor RodrigoVergara R Para medir masas en ellas, se colocan “masas patrones” (colección de objetos de masa conocida, indicadas en [Kg.] o submúltiplos de [Kg.]) en un plato de la balanza y el cuerpo que se quiere “masar” en el otro. Cuando los platos estén equilibrados, podemos determinar Pesas para balanzas Balanza de platos la masa del cuerpo sumando las masas patrón. Las básculas se usan para medir masas de mayor valor. Típicamente tienen una plataforma a ras de suelo, donde resulta fácil colocar la masa que se quiere medir. Balanza electrónica Balanza de cocina Figura 3) Algunos tipos de balanzas Existen dos tipos de básculas: • Las mecánicas, basada en un juego de palancas que se activaban al colocar la masa en la plataforma y que luego se equilibra con el desplazamiento de una aguja conectada a un resorte pilón a Báscula de pesaje para vehículos Báscula de baño lo largo de una barra pesados graduada donde se lee la Figura 4) Algunos tipos de básculas masa. • Las electrónicas, que utilizan un sensor (mejor conocido como celda de carga) que varía su resistencia conforme aumenta o disminuye la masa sobre ellas. La romana es aún usada por vendedores ambulantes, aunque ya está quedando obsoleta. Es un instrumento ligero y fácil de manipular, aunque su exactitud no es muy grande. Su principio de funcionamiento está basado en la Ley de Hooke, donde el peso de una materia se contrarresta con la fuerza de compresión de un resorte a lo largo de la regla graduada. La materia que se va a pesar se coloca en un plato o se cuelga de los ganchos que tienen. Para mayor exactitud de la medición obtenida, la romana debe colocarse totalmente en posición vertical, efecto que se obtiene moviendo el pilón de la romana a lo largo de la regla graduada, en el punto de la regla que está situado el pilón cuando la barra graduada está totalmente horizontal se lee directamente el peso de la mercancía que se pesa. Figura 5) Romana de muelle Introducción a la Física Paralelos 10 y 13. Profesor RodrigoVergara R Masa y relatividad Con la introducción de la teoría de relatividad, el concepto de masa fue reexaminado. Se ha demostrado que la masa de cada partícula aumenta con la rapidez según: mv (v ) = Donde • • • • m0 ( c) 1− v 2 c: rapidez de propagación de la luz en el vacío. v: rapidez de la partícula. m0: masa de la partícula cuando está en reposo. mv: masa de la partícula cuando se mueve con rapidez v. La variación de la masa con la rapidez del cuerpo se aprecia en la figura 3. Figura 6) Relación entre masa y Para todas las aplicaciones de la vida diaria y en la práctica velocidad corriente en la ingeniería, en donde las velocidades son mucho menores que la de la luz, podemos considerar que la masa de un cuerpo es constante. 5 6 Introducción a la Física Paralelos 10 y 13. Profesor RodrigoVergara R 2) Densidad • Definir y aplicar los conceptos: densidad de un objeto y densidad de un material. • Conocer y usar unidades de densidad kg/dm3 = g/cm3 • Conocer y usar los conceptos: densidad volumétrica, densidad superficial y densidad lineal. • Conocer y usar los conceptos: densidad de sólidos, de líquidos y de gases • Conocer y usar el concepto densidad de cosas. • Plantear y resolver problemas de masa y densidad. Introducción. El tamaño o volumen de un objeto no puede ser usado como medida de la masa del objeto. Por ejemplo, una bola (esfera) de acero puede perfectamente tener el mismo diámetro de una pelota de tenis de mesa (ver figura 7), pero sus masas van a ser evidentemente diferentes. Asimismo, 1 [kg] de acero no tiene el mismo volumen de 1 [kg] de agua. M1 M 2 M M = = = i = = n = ρ mat V1 V2 Vi Vn Estos cuocientes definen una propiedad del material de que está confeccionado el cuerpo: la densidad del material, que es la masa por unidad de volumen de un cuerpo homogéneo confeccionado con ese material. La densidad volumétrica de un cuerpo se mide típicamente en: • [Kg./m3] (Sistema MKS) • [g/cm3] (Sistema CGS) • [Kg./dm3] ó [Kg./litro] (la más usada) kg g kg Equivalencia: 1 ≡ 1 3 ≡ 10 3 3 3 dm cm m En las siguientes tablas se muestran valores de densidad para diversos cuerpos sólidos, líquidos y gaseosos Figura 7) Pelotas de tenis de mesa v/s Bolas de acero Se necesita establecer una relación entre la masa y el volumen de un objeto. Un método útil para comparar cantidades físicas es establecer el cuociente entre ellas. Eso es lo que se conoce como la densidad (volumétrica) de un cuerpo Densidad media de un cuerpo En general, los cuerpos están compuestos de diferentes tipos de materiales, y tienen una forma irregular. Consideremos el caso de un cuerpo sólido con una cavidad interior. Suponiendo que la cavidad esté vacía, podemos definir la “densidad media del material” como: ρobjeto = Introducción a la Física Paralelos 10 y 13. Profesor RodrigoVergara R mobjeto masa del objeto = volumen del objeto v objeto Mobj, Vobj Materiales sólidos Material Aluminio Zinc Hierro Acero Bronce Cobre Plata Plomo Oro Platino Figura 8) Cuerpo de forma irregular Densidad de un material En un cuerpo homogéneo las masas de porciones del cuerpo que tiene igual volumen son iguales. Si en distintas zonas de cuerpo homogéneo como el de la figura 9 se toman N “pedazos” de volúmenes V1, V2, …., VN, sus masas M1, M2, …, MN son tales que: Figura 9) Cuerpo homogéneo ρ [g/cm3] 2,70 7,20 7,80 7,83 8,50 8,90 10,60 11,40 19,30 21,50 Material Hielo Arcilla Vidrio Cuarzo Mármol Diamante Corcho Pino Roble Hulla Azúcar ρ [g/cm3] 0,92 2,00 2,50 2,60 2,70 3,50 0,30 0,40 0,70 1,30 1,60 Materiales líquidos Material ρ [g/cm3] Agua Gasolina Éter Alcohol Etílico 1,00 0,70 0,74 Benceno 0,80 Kerosene 0,88 0,79 Material Agua de mar Leche Glicerina Tetracloruro de carbono Ácido Sulfúrico Yoruro de Metileno Mercurio ρ [g/cm3] 1,0250 1,0310 1,2600 1,6000 1,8400 3,3000 13,6000 7 8 Introducción a la Física Paralelos 10 y 13. Profesor RodrigoVergara R Materiales gaseosos Material Hidrógeno ρ [kg/m3] Metano Nitrógeno Aire Etano 0,72 1,25 1,29 1,36 Material Oxígeno Bióxido de carbono Propano Kriptón Xenón Radón 0,09 ρ [kg/m3] 1,43 Densidad Lineal 1,98 2,02 3,70 5,85 9,73 Considere una barra o alambre, donde una de las dimensiones (la longitud) es mucho mayor que las otras dos. Observaciones. • Salvo el mercurio, los líquidos tienen en general menor densidad que los sólidos. • Los gases tienen densidades tres órdenes de magnitud menores que los sólidos y líquidos. Así, en cualquier situación donde hayan mezclados sólidos y líquidos con gases, la densidad de estos últimos se puede despreciar. Para un cuerpo compuesto de dos materiales homogéneos (ver figura 10) de masas M1 y M2, volúmenes V1 y V2 y densidades ρ1 y ρ2, la densidad media está dada por M M + M 2 ρ1V1 + ρ 2V2 ρ = total = 1 = Vtotal V1 + V2 V1 + V2 ρ= M total = Vtotal ∑M ∑V ∑ρ V n n =1 N n = n n =1 M M 1 M 1 = = ⋅ = ⋅λ V Ltr ⋅ Ast Ast Ltr Ast M barra barra La idea de densidad también puede ser aplicada a diversas cosas con el fin de establecer cuocientes de comparación. Así, hablamos por ejemplo de “partículas por metro cúbico”, “ovejas por hectárea”, “automóviles por habitante”, etc. n Ejemplos: • n =1 N ∑V ρ= Figura 12) Barra o alambre Densidad de cosas Figura 10) Cuerpo compuesto por dos materiales homogéneos N Sea una barra homogénea, de longitud Ltr y área de sección transversal “Ast” constante y uniforme. Se puede establecer que donde λ es la densidad lineal de la barra, que se define como λ = Para un cuerpo compuesto de N materiales homogéneos (ver figura 10) de masas M1, M2,…y MN, volúmenes V1, V2,…y VN y densidades ρ1, ρ2,…y ρN, la densidad media está dada por N Introducción a la Física Paralelos 10 y 13. Profesor RodrigoVergara R M plancha donde σ es la densidad superficial de la plancha, que se define como σ = Aplancha n Chile continental tiene un área de 756.523 [km2], y sus habitantes en 1975 estaban estimados en 10.557.000. Con estos datos, podemos decir que la densidad media de población del país es de: n =1 Densidad Superficial D= Considere una plancha o lámina como la de la figura 11, en la cual una de las dimensiones (el espesor) es mucho menor que las otras dos Sea una plancha homogénea y con espesor “e” constante y uniforme. Consideremos un trozo de la plancha de área Atr. Se puede establecer que ρ= M M 1 M 1 = = ⋅ = ⋅σ V e ⋅ Atr e Atr e Población [Habitante ] 10557000 habitante habitante = ≈ 14 2 2 2 A Km 756623 km km [ ] Es muy conocido el hecho de que la densidad de habitantes cambia en las diferentes zonas de Chile. Mientras en la Región Metropolitana es muy grande, en las zonas extremas (Arica, Aysén) es muy baja. Figura 11) Plancha o lámina • En una propaganda de pinturas nos dicen que un galón sirve para cubrir 60 [m2]. Sabiendo que un galón equivale aproximadamente a 3,8 [litro], podemos calcular el rendimiento de la pintura en [m2/litro]. Rendimiento de la pintura = [ ] m2 60 m 2 ≈ 16 3,8 [litro ] litro