Problema disco con barra
Anuncio
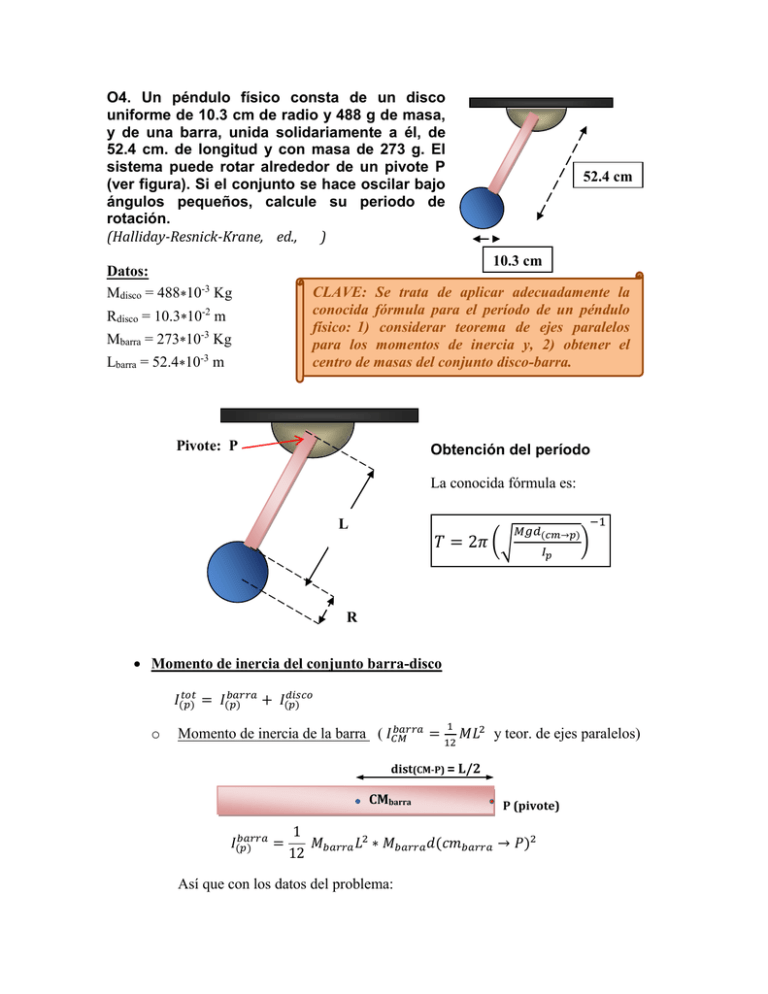
O4. Un péndulo físico consta de un disco uniforme de 10.3 cm de radio y 488 g de masa, y de una barra, unida solidariamente a él, de 52.4 cm. de longitud y con masa de 273 g. El sistema puede rotar alrededor de un pivote P (ver figura). Si el conjunto se hace oscilar bajo ángulos pequeños, calcule su periodo de rotación. (Halliday-Resnick-Krane, ed., ) Datos: Mdisco = 488*10-3 Kg -2 Rdisco = 10.3*10 m Mbarra = 273*10-3 Kg Lbarra = 52.4*10-3 m 52.4 cm 10.3 cm CLAVE: Se trata de aplicar adecuadamente la conocida fórmula para el período de un péndulo físico: 1) considerar teorema de ejes paralelos para los momentos de inercia y, 2) obtener el centro de masas del conjunto disco-barra. Pivote: P Obtención del período La conocida fórmula es: L 𝑇 = 2𝜋 (√ 𝑀𝑔𝑑(𝑐𝑚→𝑝) 𝐼𝑝 −1 ) R Momento de inercia del conjunto barra-disco 𝑡𝑜𝑡 𝑏𝑎𝑟𝑟𝑎 𝑑𝑖𝑠𝑐𝑜 𝐼(𝑝) = 𝐼(𝑝) + 𝐼(𝑝) o 1 𝑏𝑎𝑟𝑟𝑎 Momento de inercia de la barra ( 𝐼𝐶𝑀 = 12 𝑀𝐿2 y teor. de ejes paralelos) dist(CM-P) = L/2 CM cmbarra barra 𝑏𝑎𝑟𝑟𝑎 𝐼(𝑝) = P (pivote) 1 𝑀𝑏𝑎𝑟𝑟𝑎 𝐿2 ∗ 𝑀𝑏𝑎𝑟𝑟𝑎 𝑑(𝑐𝑚𝑏𝑎𝑟𝑟𝑎 → 𝑃)2 12 Así que con los datos del problema: 1 𝑏𝑎𝑟𝑟𝑎 𝐼(𝑝) = [12 (0.273 ∗ 0.5242 ) + 0.273 ∗ 0.2622 ] = 0.02499 Kg.m2 o 1 𝑑𝑖𝑠𝑐𝑜 Momento de inercia de la barra ( 𝐼𝐶𝑀 = 12 𝑀𝐿2 y teor. de ejes paralelos) CMdisco P (pivote) dist (cmdisco-pivote) = R + L 𝑑𝑖𝑠𝑐𝑜 𝐼(𝑝) = 1 𝑀 𝑅 2 ∗ 𝑀𝑑𝑖𝑠𝑐𝑜 𝑑(𝑐𝑚𝑑𝑖𝑠𝑐𝑜 → 𝑃)2 2 𝑑𝑖𝑠𝑐𝑜 1 𝑑𝑖𝑠𝑐𝑜 𝐼(𝑝) = [2 (0.488 ∗ 0.1032 ) + 0.488(0.524 + 0.103)2 ] = 0.1944 Kg.m2 o Momento de inercia total Centro de masas del conjunto barra-disco Hemos de recordar que si un objeto sólido se divide artificial o realmente en partes podemos aplicar, para el cálculo del centro de masas, una fórmula similar a la del centro de masas de un conjunto de masas puntuales (supòngamos que lo dividimos en 4 partes): 𝑡𝑜𝑡 𝐼(𝑝) = 0.2194 𝐾𝑔𝑚2 CMparte1 CMparte2 𝑟⃗ 𝑐𝑚1 CMparte3 𝑟⃗ 𝑐𝑚2 𝑟⃗ 𝑐𝑚3 𝑟⃗ 𝑐𝑚3 CMparte4 𝑟⃗ 𝑐𝑚4 𝑟𝑐𝑚 = 𝑟𝑐𝑚1 𝑀1 + 𝑟𝑐𝑚2 𝑀2 + 𝑟𝑐𝑚3 𝑀3 + 𝑟𝑐𝑚4 𝑀4 𝑀1 + 𝑀2 +𝑀3 + 𝑀4 Dividimos entonces nuestro cuerpo dos partes, las dos naturales del mismo (y ello, porque de cada una conocemos la ubicación de su centro de masas). Para facilitar el trabajo algebraico, colocamos nuestro sistema de coordenadas en el centro del disco, tal como muestra la figura. Entonces la fórmula que se adapta nuestro caso evidentemente será: 𝑟𝑐𝑚 (𝑑) (𝑏) 0 ∗ 𝑀𝑑 + (𝐿⁄2 + 𝑅)𝑀𝑏 𝑟𝑐𝑚 𝑀𝑑 + 𝑟𝑐𝑚 𝑀𝑏 = = 𝑀𝑑 + 𝑀𝑏 𝑀𝑑 + 𝑀𝑏 𝑟𝑐𝑚 = (0.262 + 0.103) ∗ 0.273 = 0.1312𝑚 0.723 + 0.488 Finalmente, el valor del perìodo o 𝑀𝑡𝑜𝑡 = 𝑀𝑑𝑖𝑠𝑐𝑜 + 𝑀𝑏𝑎𝑟𝑟𝑎 = 0.488 + 0.273 = 0.761 𝐾𝑔 o d(CM → P) = L + R − 𝑟𝐶𝑀 = (0.540 + 0.103) − 0.1312 = 0.4960 𝑡𝑜𝑡 o 𝐼(𝑝) = 0.2194 𝐾𝑔𝑚2 (antes calculado) Entonces: 𝐓 = 2π (√ 0.761∗9.8∗0.4960 0.2194 −1 ) = 1.53 s










