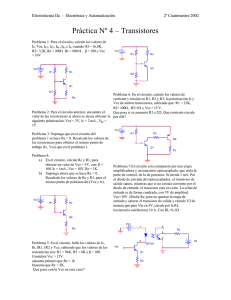
circuitos con dispositivos de dos terminales

UNIVERSIDAD NACIONAL EXPERIMENTAL POLITÉCNICA
ANTONIO JOSÉ DE SUCRE”
VICERRECTORADO BARQUISIMETO
DEPARTAMENTO DE INGENIERÍA ELECTRÓNICA
APUNTES DE ELECTRÓNICA I
EL1154
Dimas Mavares T.
Barquisimeto, Mayo de 2000
i
INTRODUCCIÓN ........................................................................................................................................................................ III
CIRCUITOS CON DISPOSITIVOS DE DOS TERMINALES ..................................................................................................... 1
MODELOS DE DISPOSITIVOS DE DOS TERMINALES ........................................................................................................................ 1
Introducción ........................................................................................................................................................................... 1
Métodos de análisis ................................................................................................................................................................ 2
DIODOS DE UNIÓN PN................................................................................................................................................................... 7
Métodos de análisis ................................................................................................................................................................ 7
DIODO ZENER ............................................................................................................................................................................ 10
CIRCUITOS RECORTADORES (LIMITADORES)............................................................................................................................. 12
CIRCUITOS RECTIFICADORES..................................................................................................................................................... 14
Rectificador de media onda.................................................................................................................................................. 14
Circuito demodulador AM.................................................................................................................................................... 16
Rectificadores de onda completa.......................................................................................................................................... 17
Fuente de alimentación con carga no resistiva .................................................................................................................... 17
CIRCUITOS CONFORMADORES.................................................................................................................................................... 21
P.1) Análisis dado un circuito, para determinar iS /vS .......................................................................................................... 22
P.2) Análisis dado un circuito, para determinar vo /vS ......................................................................................................... 27
P.3) Síntesis de un circuito a partir de su característica iS /vS ............................................................................................. 29
CIRCUITOS CON DISPOSITIVOS DE TRES TERMINALES ................................................................................................. 35
INTRODUCCIÓN .......................................................................................................................................................................... 35
MODELO DEL BJT PARA BAJAS FRECUENCIAS .......................................................................................................................... 36
Resistencia en pequeña señal del puerto de salida .............................................................................................................. 37
Modelo de transconductancia del BJT ................................................................................................................................. 37
Resistencia en pequeña señal del puerto de entrada del BJT............................................................................................... 38
Modelo del BJT considerando regiones distintas a la activa............................................................................................... 38
Dependencia de los BJTs de la temperatura ........................................................................................................................ 39
TRANSISTORES DE EFECTO DE CAMPO (FETS) ........................................................................................................................... 39
MOSFET incremental o de enriquecimiento ........................................................................................................................ 39
MOSFET decremental o de empobrecimiento...................................................................................................................... 40
Transistor de efecto de campo de unión (JFET) .................................................................................................................. 40
Transistor de efecto de campo de metal semiconductor (MESFET) de arseniuro de galio (GaAs).....................................41
Modulación de la longitud del canal.................................................................................................................................... 41
FETs canal p ........................................................................................................................................................................ 42
Modelo de FETs para bajas frecuencias.............................................................................................................................. 42
Dependencia de los FETs de la temperatura ....................................................................................................................... 43
POLARIZACIÓN DE DISPOSITIVOS DE TRES TERMINALES............................................................................................................. 44
Conceptos fundamentales..................................................................................................................................................... 44
a) Método analítico .............................................................................................................................................................. 46
b) Método gráfico................................................................................................................................................................. 48
c)Método de linealización por tramos.................................................................................................................................. 50
TÉCNICAS DE POLARIZACIÓN PARA LOS BJTS ........................................................................................................................... 53
Conceptos básicos ................................................................................................................................................................ 53
Polarización fija ................................................................................................................................................................... 54
Polarización fija con estabilidad mediante resistencia de emisor ....................................................................................... 56
Estabilidad de polarización mediante resistencia de emisor ............................................................................................... 58
Estabilización mediante resistencia de realimentación entre colector y base ..................................................................... 61
Estabilización mediante diodos............................................................................................................................................ 61
Técnicas de polarización de FETs ....................................................................................................................................... 63
Polarización fija ................................................................................................................................................................... 64
Autopolarización y polarización fija combinadas (estabilización mediante resistencia de surtidor) .................................. 64
Polarización de FETs como fuente de corriente .................................................................................................................. 65
Estabilización mediante resistencia entre drenador y fuente............................................................................................... 65
Polarización de un amplificador NMOS .............................................................................................................................. 66
ANÁLISIS DE PEQUEÑA SEÑAL EN CIRCUITOS CON DISPOSITIVOS DE TRES TERMINALES ................................ 67
TIPOS DE AMPLIFICADORES ....................................................................................................................................................... 67
Amplificadores de voltaje..................................................................................................................................................... 67
ii
Amplificadores de corriente ................................................................................................................................................. 68
Amplificadores de transresistencia ...................................................................................................................................... 68
Amplificadores de transconductancia .................................................................................................................................. 69
ANÁLISIS DE PEQUEÑA SEÑAL EN CIRCUITOS CON DISPOSITIVOS DE TRES TERMINALES ............................................................. 69
Análisis lineal de circuitos de con BJTs............................................................................................................................... 71
Rectas de carga de DC y AC ................................................................................................................................................ 79
Circuitos con FETs............................................................................................................................................................... 80
AMPLIFICADORES DE TRANSISTORES EN CASCADA .................................................................................................................... 84
Comparación de configuraciones de amplificadores con BJTs ........................................................................................... 84
Comparación de configuraciones de amplificadores con FETs........................................................................................... 85
ANÁLISIS DE POTENCIA EN CIRCUITOS CON DISPOSITIVOS DE TRES TERMINALES ............................................. 89
CONCEPTOS FUNDAMENTALES .................................................................................................................................................. 89
Distorsión:............................................................................................................................................................................ 89
Distorsión armónica............................................................................................................................................................. 90
Eficiencia.............................................................................................................................................................................. 90
CONFIGURACIÓN DE SALIDA CON POLARIZACIÓN LINEAL (CIRCUITO TIPO A) ............................................................................ 91
CONFIGURACIÓN DE SALIDA DE PAR COMPLEMENTARIO (AMPLIFICADOR TIPO B)..................................................................... 92
AMPLIFICADOR CLASE AB......................................................................................................................................................... 94
Polarización de amplificadores completarios tipo AB ......................................................................................................... 95
Circuito manejador (driver stage)........................................................................................................................................ 97
BIBLIOGRAFÍA .......................................................................................................................................................................... 98
iii
INTRODUCCIÓN
El propósito de este trabajo es proporcionar al estudiante de la materia ELECTRÓNICA I. EL-1154, de la
UNEXPO VR BARQUISIMETO, de una guia de estudios completa y ordenada. El material que aquí se presenta es
una recopilación de temas que aparecen normalmente en la literatura, por lo que la intensión de publicar estos
apuntes es la de guiar al estudiante de manera acorde a la forma como se imparte la materia ELECTRÓNICA I en
nuestra Universidad, más que presentar material novedoso. Por otra parte, se ha hecho incapié en las explicaciones
que normalmente causan confusión al estudiante, incluyendo ejemplos que pueden ser aclaratorios.
El primer capítulo trata sobre circuitos con dispositivos de dos terminales. En primer lugar se estudian los
métodos de análisis de dispositivos genéricos (ficticios) de dos terminales, particularizando luego para diodos de
unión pn, tratándolos como un caso particular de los dispositivos genéricos. Más adelante se describe el
funcionamiento de diodo zener, para que puedan ser estudiados circuitos recortadores y fuentes de alimentación que
los incluyan. Por último se estudian los circuitos conformadores, usando métodos gráficos y analíticos para hallar su
característica corriente-tensión o de transferencia o sintetizarlos a partir de ellas.
El segundo capítulo trata sobre circuitos con dispositivos de tres terminales. Se analizan los circuitos usando los
mismo métodos que en el capítulo 1, usando también dispositivos genéricos. Luego se analizan las características de
entrada y salida de los BJTs y los FETs, para poder hallar los modelos tanto de polarización como de pequeña señal
de estos dispositivos. Más adelante se estudia la polarización de circuitos con BJTs, incluyendo configuraciones que
mediante realimentación contribuyen a la estabilización del punto de polarización, analizandolos y sintetizandolos si
se especifican los puntos de polarización deseados para diferentes temperaturas o cambios de los parámetros del
dispositivo. Por último se estudia la polarización de circuitos con FETs y los FETs usados como fuentes de
corriente o cargas no lineales.
El tercer capítulo trata sobre el análisis de pequeña señal de circuitos con dispositivos de tres terminales,
describiendo brevemente los diferentes tipos de amplificadores clasificados en función de las señales de entrada y
salida. Seguidamente se particulariza para circuitos con BJTs, estudiandose las configuraciones de emisor común,
colector común y base común, para hallar la resistencia de entrada, de salida y las ganancias de corriente, tensión,
transresistencia y transconductancia. Por último se hace el mismo tratamiento para circuitos con FETs.
El cuarto y último capítulo trata sobre análisis de potencia en circuitos con dispositivos de tres terminales,
restringuiendose a circuitos de potencia con BJTs. Se habla primero de los conceptos fundamentales en el análisis
de potencia, como distorsión y eficiencia, para luego describir y analizar los circuitos tipo A, B y AB.
Quisiera agradecer a mis padres, Hernán y Margarita, a mis hermanos Ricardo y Andreína, a Jorge Aguero y
Roberto Uzcátegui por su amistad incondicional, y a los profesores Jesús Machado y Rafael Sánchez por sus
explicaciones y recomendaciones.
1
CIRCUITOS CON DISPOSITIVOS DE DOS TERMINALES
Modelos de dispositivos de dos terminales
Introducción
Los circuitos que contienen elementos no lineales no necesariamente tienen que ser resueltos mediante cálcullos
matemáticos directos. Se pueden aplicar los siguientes métodos:
a) Método analítico
b) Método gráfico
c) Método de linealización por tramos
La selección del método depende de:
la exactitud deseada
la disponibilidad de datos, como curvas y expresiones que caractericen el funcionamiento de los dispositivos.
Al obtener soluciones exactas, deben tomarse en cuenta la variabilidad de los dispositivos aún cuando sean del
mismo tipo
iii. la disponibilidad de potencia de cómputo.
i.
ii.
Nota: las convenciones utilizadas en este curso son:
– Letras mayúsculas con subíndices en mayúsculas para valores constantes o señales DC. Por ejemplo, VTR para
voltaje umbral (constante) o VS para la componente DC de vS
– Letras minúsculas con subíndices en minúsculas para señales AC. Por ejemplo, vs para la componente AC de vS
– Letras minúsculas con subíndices en mayúsculas para señales totales (niveles AC y DC). Por ejemplo, vS
– Letras mayúsculas con subíndices duplicados en mayúsculas para fuentes o valores DC en un punto del circuito.
Por ejemplo, VCC para una fuente de tensión DC ubicada en el terminal C de un circuito o para un voltaje DC en
el punto C de un circuito.
– Dispositivos no lineales
Su representación se hace mediante ecuaciones no lineales. Al analizar el funcionamiento de circuitos que
incluyan estos dispositivos, no debe aplicarse el teorema de superposición, que es válido sólo para sistemas lineales.
Al utilizarse equivalentes de Thevening y/o Norton, no se deben incluir dispositivos no lineales dentro de la sección
del sistema a sustituir mediante el circuito equivante. Sin embargo, se recomienda en general el uso los equivalentes
de Thevening y/o Norton, siempre que la sección a sustituir esté compuesta sólo por elementos lineales.
ƒ
Ejemplo de dispositivo no lineal: dispositivo de ley cuadrática
El dispositivo de ley cuadrática es un dispositivo genérico, caracterizado por las siguientes expresiones:
iS (mA)
 A(v S − VTR ) 2 ∀v S ≥ VTR
iS = 
0
∀v S < VTR
donde :VTR = voltaje umbral
(2.1)
iS
+
vS
-
A(vS - VTR) 2
A = factor de escala
vS - VTR
Fig. 2.1. Dispositivo de ley cuadrática
vS (V)
2
En la figura 2.1 podemos observar la representación del dispositivo de ley cuadrática y su característica corriente
tensión (i/v). Nóte que la corriente es igual a cero a menos que se supere el voltaje umbral VTR. A partir de este
valor, el incremento de corriente será una función no lineal de la tensión en exceso vS - VTR . Para comprender
porqué no es válido el teorema de superposición, supongamos que se aplica una tensión ∆V, de tal forma que el
voltaje en exceso sea ∆V - VTR , al cual corresponde un incremento de corriente ∆Ι1. Si aplicamos en seguida otro
incremento ∆V, el voltaje en exceso será 2∆V - VTR y el incremento de corriente será ∆Ι2 ≠ ∆Ι1. Para que sea válido
el teorema de superposición, es necesario que iguales incrementos de voltaje produzcan iguales incrementos de
tensión, sin importar el punto donde opere el dispositivo, de donde concluimos que la aplicación del teorema de
superposición en este caso conducirá a resultados erróneos.
Apliquemos ahora los distintos métodos de solución a circuitos que incluyan el dispositivo de ley cuadrática
Métodos de análisis
Método analítico
5 kΩ
10 kΩ
iS
iS
12 V
110 kΩ
+
vS
-
+
vS
-
6V
a)
b)
Fig. 2.2. a) circuito simple con dispositivo de ley cuadrática como carga b) equivalente de Thevening
Donde el dispositivo de ley cuadrática tiene las siguientes características: A = 1 mA/V2 y VTR = 0 V
Primero supongamos que el dispositivo de ley cuadrático opera en la zona de vS ≥ VTR, entonces
 A(v S − VTR ) 2

⇒ v S 2 + 0.2v S − 1.2 = 0 ⇒ v s = 1 V
(2.2)
iS =  6 − v S
- 1.2 V
 5 k
Note que la solución a la ecuación cuadrática resultante arroja dos resultados: el resultado positivo es tal que está
de acuerdo con la suposición que tomamos, o sea, que vS es mayor que cero, mientras que la restante nos dice que vS
es menor que cero, lo que contradice nuestra suposición. Note también que la segunda solución corresponde a un
punto imposible de funcionamiento del dispositivo, ya que para todo valor de vS menor que cero, la corriente iS debe
ser igual a cero, y sin embargo, si sustituimos el valor de vS obtenido para encontrar la corriente en el dispositivo en
la ecuación utilizada, tenemos que iS = Av s 2 = 1.44 mA , lo que nos lleva a una contradicción. Esta contradicción
debe interpretarse como una solución matemáticamente correcta, pero fisicamente imposible para este sistema.
Luego, concluimos que iS = 1 mA, y el punto de funcionamiento del dispositivo es (iS , vS) = (1 mA, 1 V).
Generalmente las expresiones resultantes de combinar las características del dispositivo y del circuito son
demasiado complicadas como para ser resueltas simbolicamente y luego evaluadas. Por lo tanto, es necesario
apoyarse en métodos iterativos que nos permitan hallar las raices de una expresión sin resolverla simbolicamente.
Uno de estos métodos es el de Newton-Raphson; veamos como se aplica en nuestro caso. Combinando las
ecuaciones del sistema 2.2, tenemos que
v S 2 + 0 .2 v S − 1 .2 = 0
Si definimos una función de error f(vS) tal que el error en la i-ésima iteración esté dado por
E i = f (v S ) v = v
S
Si
deseamos que este error sea lo más próximo posible a cero. Por lo tanto, en nuestro caso
f ( v S ) = v S 2 + 0 .2 v S − 1 .2
(2.3)
(2.4)
(2.5)
3
Luego, concluimos que, dado un sistema de ecuaciones, lo reducimos a una sola expresión y la igualamos a cero,
siendo esta nuestra función de error. Esta función de error la podemos evaluar en distintos puntos, y los que
correspondan a las raices de la función nos darán un error próximo a cero. Ahora nos queda por resolver la cuestión
de cómo nos aproximamos a estas raices. Indudablemente debemos inicializar el método y a partir de este valor
inicial “movernos” hacia la solución, para ello usamos el método de Newton-Raphson que nos dice que la solución
en la iteración i-ésima está dada por
f ( xi −1 )
(2.6)
xi = xi −1 −
df ( x)
dx x = xi −1
lo que quiere decir que la solución en la iteración i-ésima está dada por la solución en la iteración i-ésima menos
uno menos un paso, que será directamente proporcional al error e inversamente proporcional al gradiente del error.
El factor que determina la velocidad y exactitud del método es precisamente el paso, y en el método de NewtonRaphson, al ser directamente proporcional al error, significa que al estar alejados de la solución, nos moveremos
más rapidamente hacia ella, ya que tendremos un paso mayor. Al ser el paso inversamente proporcional al gradiente
del error, significa que a medida que la función de error cambie más rapidamente, nos aproximaremos con un paso
menor, y viceversa. La principal desventaja del método de Newton-Raphson, es que es vulnerable a los óptimos
locales, por lo que si queremos hallar el óptimo global, debemos inicializar en un número considerable de puntos,
dependiendo del espacio de búsqueda en que trabajemos.
Luego
df (v S )
= 2v S + 0.2
f ( v S ) = v S 2 + 0 .2 v S − 1 .2 y
dv S
3.2
f (2)
Si tomamos como punto de inicialización v S 0 = 2 ⇒ v S1 = 2 −
=2−
= 2 − 0.7619 = 1.238 V
4.2
df (v S )
dv S
vS = 2
(el punto de inicialización se puede seleccionar aleatoriamente, sin embargo, si tenemos alguna sospecha sobre el
rango donde puede estar la solución, es conveniente escoger un punto dentro de ese rango. De la inicialización
depende la convergencia, la velocidad de convergencia y la obtención de óptimos locales o globales).
Repitiendo el procedimiento tenemos que
f (1.238)
0.58
= 1.238 −
= 1.238 − 0.2167 = 1.0212 V
v S 2 = 1.238 −
2.676
df (v S )
dv S v =1.238
S
v S 3 = 1.0212 −
f (1.0212)
df (v S )
dv S
= 1.0212 −
0.047
= 1.0212 − 0.021 = 1.000022 V
2.2423
vS =1.0212
El método también necesita un criterio de finalización, o sea, que como teoricamente sólo en un número infinito
de iteraciones podemos obtener un error igual a cero, debemos establecer cual es un error aceptable para nuestra
aplicación. En este caso, vemos que para la tercera iteración tenemos un error bastante pequeño, por lo que podemos
aceptarla como solución. En general, se calcula la diferencia entre la iteración actual y la anterior, y cuando esta
diferencia sea menor que cierto valor predeterminado, diremos que el método ha convergido, y la iteración actual
será nuestra solución.
Método gráfico
Si contamos con las gráficas de la característica i/v del dispositivo, podemos hallar el punto de funcionamiento en
forma gráfica. Cuando un dispositivo trabaja en un circuito, este le impone limitaciones en cuanto a los posibles
puntos de funcionamiento. Por ejemplo, si tenemos un circuito equivalente de Thevening como el de la figura 2.2
b), podemos concluir que cualquieras que sean las características del dispositivo que actúa como carga (en este caso
el dispositivo de ley cuadrática), el voltaje entre sus terminales no puede ser mayor que 6 V (a menos que sea un
dispositivo activo, el cual no es el caso). Otra limitación es que la corriente que circula por la carga no puede ser
4
mayor que 6 V/5 kΩ = 1.2 mA, que es el caso limite cuando la resistencia de carga es nula. El conjunto de los
posibles puntos de funcionamiento que resultan de las restricciones que impone el circuito a la carga, sin importar
las características de ella, la llamamos recta de carga; los posibles puntos forman una recta pues el circuito al que
está conectada la carga es un sistema lineal, de otra forma, los posibles puntos podrían formar lugares geométricos
distintos a una recta.
Si trazamos la recta de carga, considerando lo explicado en el párrafo anterior, y la intersectamos con la
característica i/v del dispositivo, podemos obtener en forma gráfica el punto de funcionamiento, como en la figura
2.3.
iS (mA)
vS (V)
Fig. 2.3. Punto de funcionamiento según el método gráfico
Método de linealización por tramos
Aún cuando la característica i/v de la carga sea una función no lineal, podemos analizar el sistema como si fuera
lineal si consideramos la característica como dividida en tramos, y para cada tramos hallamos un circuito
equivalente lineal con un comportamiento similar al de la carga en ese intervalo. Por ejemplo, la característica i/v
del dispositivo de ley cuadrática, la podemos dividir en intervalos, como en la figura 2.4, y hallar para cada uno de
los intervalos una función lineal equivalente. En la figura 2.5, se muestran los tramos lineales productos de la
linealización de la figura 2.4.
iS (mA)
V1
V2
Fig. 2.4. Linealización por tramos
V3
vS (V)
5
iS (mA)
iS (mA)
Para vS < 0
Para 0 < vS < V1
1/R1
vS (V)
iS (mA)
V1
iS (mA)
Para V1 < vS < V2
Para V2 < vS < V3
1/R3
1/R2
V1
vS (V)
V2 vS (V)
V2
V3 vS (V)
Fig. 2.5. Tramos lineales
Cada uno de estos tramos corresponderá a una recta, con pendiente igual a la conductancia del circuito
equivalente, y un desplazamiento en el eje vS , que corresponde a una fuente de tensión en el circuito equivalente.
Por lo tanto, podemos definir tantos tramos como deseemos en la linealización, y a cada uno de ellos asociamos un
circuito equivalente correspondiente a una resistencia y una fuente de tensión, como se muestra en la figura 2.6.
...
Do
D1
D2
Dn
Ro
R1
R2
Rn
Vo
V1
V2
Vn
...
Fig. 2.6. Estructura del circuito equivalente
Para hallar el valor de la pendiente de la recta, y por lo tanto de la resistencia en el circuito equivalente, podemos
derivar la ecuación del dispositivo en uno de los puntos del intervalo, o simplemente hallar las ecuaciones de las
rectas mediante la ecuación punto pendiente. Sabemos que para el intervalo cero, R0 = ∞ . Para el intervalo 1, V1 =
0Vy
0.4356 − 0
1
= 0.66 mmho ⇒ R 1 =
= 1.5152 kΩ
m1 =
0.66 − 0
m1
1.706 − 0.4356
para el intervalo 2, V2 = 0.66 V y
= 1.96 mmho
m2 =
1.3 − 0.66
para obtener esta pendiente, hay que añadir a R1 una resistencia en paralelo de
1
= m2 − m1 = 1.3 mmho ⇒ R 2 = 769.2 Ω
R2
1 3.61 − 1.706
para el intervalo 3, V3 = 1.3 V y
=
= 3.2 mmho ⇒ R = 312.5 Ω
R
1.9 − 1.3
6
y para obtener esta pendiente, hay que añadir a R2 una resistencia en paralelo de
1
= m3 − m2 = 1.24 mmho ⇒ R 3 = 806.5 Ω
R3
Para analizar el circuito de la figura 2.2b mediante el método de linealización por tramos, sustituimos el
dispositivo no lineal por su modelo lineal. Suponemos que el dispositivo opera en un punto tal que V2 < vS < V3 , y
por lo tanto estarán conduciendo los diodos D1 y D2, mientras D3 estará polarizado en inverso. Luego, la tensión vS
está dada por
V
6
6
.66
+ 2
+
5k R2
5 k 769.2
=
= 0.9528 V
vS =
1
1
1
1
1
1
+
+
+
+
5 k R 1 R 2 5 k 1.5152 k 769.2
Sin embargo, conocemos la solución dada por el método analítico, de donde concluimos que el error cometido fué
de ∆ = 1 - 0.9528 = 0.1699, o sea, un error del 4.96 %, lo que puede ser considerable para algunas aplicaciones.
Esto se justifica pues es precisamente alrededor de vS = 1 donde se comete el mayor error de aproximación, o sea,
donde hay mayor diferencia entre la aproximación por tramos y la característica del dispositivo; para reducir el error
podemos aumentar el número de tramos. Hagamos la linealización en el tramo número dos tomando la tangente a la
característica del dispositivo en vS = 1, y deberíamos obtener un error nulo.
D1
1.5152 Ω
0V
D2
D3
769.2 Ω
806.5 Ω
0.66 V
1.3 V
Fig. 2.7. Circuito equivalente del dispositivo de la figura 2.4
Sabemos que
m=
diS
dv S
= 2v S . Para el segundo intervalo, sea V = 1 ⇒ m2 =
vS =V
diS
dv S
= 2 mmho.
vS =1
por lo tanto, para obtener esta pendiente, hay que añadir a R1 una resistencia en paralelo de
1
= m2 − m1 mmho = 1.34 ⇒ R 2 = 746.3 Ω
R2
pero el valor de V1 también ha variado. Para hallar el nuevo valor, si queremos dejar inalterado el primer tramo,
debemos hallar la intersección de las rectas de los tramos 1 y 2, este punto es (0.7463 V, 0.5569 mA), o sea, V2 =
0.7463. Luego, vS está dado por:
6 V2
6 .7463
+
+
5 k R2
5 k .7463
=
=1V
vS =
1
1
1
1
1
1
+
+
+
+
5 k R 1 R 2 5 k 1.5152 k .7463
el cual es el resultado que esperabamos.
Note que para usar el método de linealización por tramos, debe tenerse al menos un estimado del punto de
funcionamiento, por lo que debemos tener una idea de cual es la solución. Normalmente en el análisis de circuitos
usando este método, se hace una predicción del intervalo en el que está ubicado el punto y se hace el análisis; si el
resultado está acorde con la predicción, esa es la solución, sino , se debe hacer una nueva predicción y repetir el
análisis. Este es un proceso iterativo, que concluye cuando la solución y la predicción concuerden.
7
Diodos de unión pn
Como hemos indicado en el tema I de este curso, un diodo está constituido por dos uniones, una p y una n.
Cuando se le aplica un voltaje externo, las concentraciones de portadores en las fronteras de la unión varían
exponencialmente con el voltaje aplicado, haciendo que la corriente a través del diodo sea igual a
I D = I S (e
vD / ηVT
− 1) = I S (e λvD − 1)
(2.7)
donde:
IS : Corriente de saturación (entre 10-8 y 10-14 A para diodos de Silicio)
η : Coeficiente de emisión. Toma en cuenta la recombinación en la región de agotamiento y depende del
semiconductor y la corriente de funcionamiento. Para diodos discretos con una corriente de 10 mA, η = 2, para
diodos integrados de silicio, η = 1.
VT = Voltaje equivalente térmico; VT = kT/q .
Donde:
K = 1.381 10-23 Joules/ºK (constante de Boltzman)
q = 1.602 10-19 C (carga del electrón
T = Temperatura en ºK (ºK = ºC + 273)
Luego, VT ≅ T/11600 ≅ 25 mV a 300 ºK.
Para el siguiente circuito simple con un diodo de unión pn como carga, hallemos el punto de funcionamiento
mediante los diferentes métodos estudiados. Supongamos que el diodo tiene las siguientes características:IS = 1x10-5
mA, η = 2 y T = 300 ºK.
5 kΩ
10 kΩ
iD
iD
12 V
10 kΩ
a)
+
vD
-
+
vD
-
6V
b)
Fig. 2.8. a) circuito simple con diodo de unión pn como carga b) equivalente de Thevening
Métodos de análisis
Método analítico
La recta de carga permanece igual que cuando usamos el método gráfico para analizar el circuito con el
dispositivo de ley cuadrática como carga, ya que la recta de carga no depende de ella. Sin embargo, al combinarla
con la ecuación característica del dispositivo, obtenemos una solución distinta.
 I (e vD / ηVT − 1)
 S
⇒ 0.2v D + I S e vD /ηVT − 1.2 = 0
iS =  6 − v
S

 5
Note que no es posible hallar una solución en forma cerrada para la ecuación anterior, por lo que, si deseamos
usar el método analítico, debemos recurrir a un mecanismo de búsqueda, como el de Newton-Raphson.
sustituyendo para VT = 25 mV, e IS, tenemos que
df (v D )
y
f (v D ) = 0.2v D + 1x10 −5 e 20vD − 1.2
= 2 x10 −4 e 20vD + 0.2
dv D
Inicializando en x0 = 1.5 V y después de 26 iteraciones, observamos que el algoritmo converge a x26 =
0.57968210096134 V.
8
Método gráfico
Para hallar la solución por medio del método gráfico, seguimos el mismo procedimiento que cuando analizamos el
circuito con el dispositivo de ley cuadrática, o sea, trazamos la curva característica del dispositivo y la recta de carga
en la misma gráfica, la intersección de ambas curvas nos dá el punto de funcionamiento. Una vez más, el método
gráfico presenta el inconveniente de que la precisión de la solución está limitada por la resolución de la gráfica y
por los instrumentos de medición, así como los errores de apreciación del observador. Por otra parte para la mayoría
de las aplicaciones prácticas, el error cometido es intrascendente. El resultado obtenido es de iS = 1.0841 mA y vS =
0.5796 V.
Método de linealización por tramos
Para aplicar este método debemos primero hallar linealizar por tramos la curva i/v del dispositivo, lo que podemos
hacer de la siguiente forma: si tenemos la expresión de iD en función de vD , la derivamos y evaluamos en distintos
puntos. Sabemos que para nuestro diodo (figura 2.10)
di D
= 2 x10 −4 e 20vD mA
dv D
mi =
pero
df (v D )
dv D v
D = Vi
si evaluamos en vS = 0.4, 0.5 y 0.55 V, tenemos que m1 = 0.5962 mmho ⇒ R1 = 1.6773 kΩ; m2 = 4.4053 mmho y
m3 = 11.976 mmho. Luego
1
= m2 − m1 = 3.8091 mmho ⇒ R 2 = 262.5 Ω
R2
y para el intervalo 3
1
= m3 − m2 = 7.5708 mmho ⇒ R 3 = 132.1 Ω
R3
iS (mA)
vS (V)
Fig. 2.9. Punto de funcionamiento según el método gráfico para un
circuito con diodos
Calculamos los valores de V1 , V2 y V3 , buscando el punto de intersección entre las rectas de los intervalos. De
esta forma obtenemos V1 = 0.35 V, V2 = 0.4657 V y V3 = 0.5291 V. El modelo para nuestro diodo entonces será
9
1.6773 k
0.35
262.5
806.5
0.4657
0.5291
Fig. 2.10. Circuito equivalente del diodo utilizado
iS (mA)
vS (V)
Fig. 2.11. Linealización por tramos mediante diferenciación de la
característica i/v
5 kΩ
6V
1.6773 k
0.35
262.5
0.4657
132.1
0.5291
Fig. 2.12. Circuito equivalente de la figura 2.8b.
Supongamos que la solución es tal que 0.4657 < vS < 0.5291, de donde estarán activas las dos primeras ramas del
modelo, y
V
V
6
6
0.35
0.4657
+ 1+ 2
+
+
5 k R 1 R 2 5 k 1.6773 k 262.5
=
= 0.691 V
vS =
1
1
1
1
1
1
+
+
+
+
5 k R1 R 2
5 k 1.6773 k 262.5
pero este resultado va en contra de nuestra suposición inicial; como asumimos, en función de esa suposición, que la
rama 3 estaría inactiva, y la solución contradice esa hipótesis, debemos concluir que erramos en la suposición inicial
y por lo tanto la solución no es válida, ya que aplicamos un modelo inadecuado para el dispositivo en el rango en
10
que opera. Supongamos ahora que vS > 0.529, por lo que las tres ramas estarán activas, y el punto de
funcionamiento del dispositivo está dado por
6 V1 V2 V3
6
0.35
0.4657 0.5291
+
+
+
+
+
+
5 k R 1 R 2 R 3 5 k 1.6773 k 262.5
132.1 = 0.5904 V
vS =
=
1
1
1
1
1
1
1
1
+
+
+
+
+
+
5 k R1 R 2 R 3
5 k 1.6773 k 262.5 132.1
Este resultado está de acuerdo con nuestra suposición, luego, podemos tomarlo como válido. Podemos observar
que la solución obtenida mediante el método de linealización por tramos presenta un error del 1.84 % respecto a la
solución analítica. Note que la solución está ubicada en un punto donde nos alejamos de la curva original al
linealizar, por lo tanto, si queremos aumentar la precisión, debemos añadir al menos un tramo en esa zona.
Diodo Zener
Tiene propiedades simulares a las de un diodo de unión pn. En la dirección de polarización directa, el zener
obedece la característica exponencial normal v/i, dada por
para v Z > 0
iZ = I s (e vZ / ηVT − 1)
En la región de polarización inversa, se comporta como una unión pn hasta el voltaje – VZK (voltaje zener), donde
la corriente comienza a fluir en dirección inversa. Está elaborado dopando fuertemente las regiones p y n, lo que
produce un gran campo interconstituido . En polarización inversa, este campo se incrementa, y los electrones de
enlace son arrancados de sus átomos (ruptura zener) o colisionan con otros átomos, arrancando a los electrones de
estos átomos de sus enlaces y formando iones (ruptura de avalancha). La mayoria de los zener utiliza ruptura por
avalancha, siendo solamente los que tienen un voltaje zener por debajo de los 6 V los que utilizan la ruptura zener.
Si la disipación de energía en el zener no excede un valor máximo permitido (que depende del tamaño, forma y
capacidad de disipación de calor del zener), el proceso de ruptura inversa no daña al dispositivo.
iZ
iZ (mA)
+
vZ
-
-VZK
Región de
polarización directa
- Is
Vγ
vZ (V)
Región de
polarización inversa
Región de
ruptura
inversa
Fig. 2.13. Diodo zener a) símbolo b) característica i/v
Ejemplo: Utilizando un diodo zener, diseñe un circuito de reducción de voltaje que permita un radio portátil,
diseñado para ser alimentado por una batería portatil de 9 V, sea alimentado por una batería de automóvil, que
puede variar en un rango de 12 a 13.6 V, dependiendo de la corriente consumida. La radio requiere de un máximo
de 0.5 W de energía a todo volumen.
11
R1
iZ
Vbat
iL
+
VZK
-
+
vL
-
Fig. 2.14. Circuito simple con regulación por zener
Como la radio está diseñada para ser alimentada por baterías portátiles de 9 V, entonces, vL = 9 V. Por lo tanto, si
usamos el circuito de la figura 2.14, debemos seleccionar un zener tal que VZK = 9 V. Por otra parte, la potencia
máxima (a todo volumen) es de 0.5 W, así que
P
0.5 W
= 55.56 mA
I Lmax = Lmax =
9V
vL
Para que el zener actúe como regulador, debe circular a través de él una corriente mínima. En la figura 2.13 se
puede observar que si el voltaje entre los terminales del zener es mayor que -VZK (menor en módulo que VZK), éste
sale de la región de ruptura inversa y entra en la región de polarización inversa, con una corriente Is , donde no
efectúa labores de regulación, ya que el voltaje entre sus terminales es menor a 9 V y no es capaz de drenar la
corriente excedente de la carga. Asi que debe circular una corriente mayor que cero por el zener cuando esté
actuando como regulador; el valor de ella varía entre dispositivos, pero se puede tomar un valor de 1 mA para la
mayoría de los zener. Luego, sea IZmin = 1 mA. Además
V − vL
e I1 = i L + iZ
I 1 = bat
R1
vemos que I1 varía con Vbat , pero el valor de esta tensión varía entre 12 y 13.6 V, entonces ¿que valor de Vbat
debemos tomar para calcular I1?. La respuesta es que depende de para que usamos I1. Tengamos en cuenta que por
R1 circula la corriente que alimenta la carga, y por lo tanto, si queremos asegurar que la corriente de carga sea de,
por ejemplo, 55.56 mA, debemos pensar en el peor de los casos, esto es, cuando la tensión en la bateria caiga a 12
V, en cuyo caso I1 será menor que cualquier otro, y si el valor de la bateria fuese mayor de 12 V, la corriente
excedente a 55.56 mA que circule por I1 se drenará por el zener. Luego
12 − 9
e i Zmin = I 1min − i Lmax = 1 mA
I 1min =
R1
12 − 9
⇒
− 55.56 = 1 ⇒ R 1 = 53 Ω ≈ 51 Ω
R1
la aproximación de R1 a 51 Ω la hacemos para especificar un valor estándar de resistencia en el diseño. Pudimos
haber aproximado a 56 Ω, pero si aumentamos la resistencia al aproximarla, obtendremos una corriente menor a la
especificada, lo que no es conveniente en este caso. Por lo tanto, la aproximación correcta es para un valor por
debajo del calculado.
Calculemos la corriente máxima en el zener
13.6 − 9
− 0 = 90.2 mA
i Zmax = I1max − i Lmin =
51
y la potencia en el zener será
PZmax = I Zmax VZK = 0.8118 W
la potencia disipada en R1 es
(13.6 − 9) 2
= 0.4149 W
PR1max =
51
Una solución al problema es: Zener con VZK = 9 V y 1 W. Resistor de 51 Ω y 0.5 W.
12
Circuitos Recortadores (Limitadores)
Los circuitos recortadores se emplean para seleccionar la parte de una onda arbitraria que esté por encima o por
debajo de un nivel de referencia.
En la figura 2.15 se muestra un circuito recortador y función de transferencia del sistema y señales de entrada y
salida. Empleando el modelo lineal aproximado, se obtiene la característica de transferencia mostrada de la
siguiente forma. Si el diodo no conduce la tensión en sus terminales será vD < Vγ y vi < Vγ + VR. Por otra parte, con
el diodo bloqueado no hay corriente en R y vo = vi. Para vi > Vγ + VR
vo
vo
Rf
Rf + R
Vγ + VR
vi
t
Vγ + VR
vi
R
+
+
vi
-
vo
VR
-
t
Fig. 2.15. Circuito recortador con diodo
R
R
+
+
vi
-
vo
+
+
vi
-
Rf
vo
VR + Vγ
a)
b)
Fig. 2.16. Circuitos resultantes en función de los estados del diodo
13
vi
R
+
+
vi
-
t
vo
VR
vo
t
VR
a)
vi
R
+
+
vi
-
t
vo
VR
vo
t
VR
b)
vi
R
t
+
+
vi
-
vo
-VR
R
t
-VR
+
+
vi
-
t
-
c)
vi
vo
vo
vo
-VR
d)
t
-VR
-
Fig. 2.17. Circuitos recortadores con diodo
En la figura 2.17 se muestra varios circuitos recortadores o limitadores. Las figuras 2.17 a) y c) corresponden a
recortadores de la parte superior de la señal de entrada, variando entre ellas solamente el nivel de referencia, como
en c) el nivel es más bajo, el diodo conducirá para valores superiores a –VR ; el funcionamiento de ambos circuitos
es idéntico. Las figuras 2.17 b) y d) corresponden a recortadores del nivel inferior de la señal, variando entre ellas
solamente el nivel de referencia.
El recorte a dos niveles se puede conseguir combinando los circuitos de la figura 2.17 o utilizando diodos zener,
con lo que se logran circuitos más sencillos, como en la figura 2.18.
La fijación consiste en desplazar la señal de entrada de tal forma que quede montada sobre un nivel DC. La figura
2.19 muestra un circuito sencillo de fijación. Cuando se conecta la señal de entrada, podemos suponer que el
capacitor C está descargado, y durante el intervalo en que la señal de entrada es positiva, el capacitor se cargará
hasta un voltaje Vm – VR, donde Vm es el voltaje pico de la señal de entrada. En lo sucesivo el capacitor no tendrá
una ruta por la cual descargarse, así que mantendrá su carga y la salida estará dada por Vi – VC = Vi – (Vm – VR), o
14
sea, una réplica de la entrada desplazada en Vm – VR , o sea, fijada en VR. Podemos también fijar la señal a un nivel
superior si cambiamos la polaridad del diodo.
vi
R
VZK2
DZ1
+
vi
-
t
vo
+
vo
t
-VZK1
DZ2
-
Fig. 2.18. Circuito recortador de dos niveles con diodos zener
C
vi
+
t
vo
VR
+
vi
-
vo
t
VR
Fig. 2.19. Circuito fijador
Circuitos Rectificadores
La función de estos circuitos es cambiar un voltaje de entrada bipolar en un voltaje de salida unipolar.
Rectificador de media onda
Se puede consturir un circuito rectificador partiendo de cualquier elemento que solamente permita el flujo de
corriente en una dirección. El tipo más sencillo es el rectificador de media onda.
rd
Vγ
Si vi > Vγ
+
D
+
+
vi
-
Carga
a)
vo
-
+
vi
-
Carga
vo
-
Si vi < Vγ
+
+
vi
-
Carga
b)
Fig. 2.20. Circuito rectificador de media onda a) diagrama circuital b)
circuitos equivalentes
vo
-
15
 RL
(vi − Vγ ) para vi > Vγ

Si la carga es resistiva, v o =  R L + rd
0
para vi < Vγ

La gráfica de la función de transferencia del rectificador de media onda se muestra en la figura 2.21
RL
R L + rd
vo
vi
Vγ
Fig. 2.21. Función de transferencia del retificador de media onda
de la figura 2.20 con una carga resistiva
D
+
RL
vi
vo
-
Fig. 2.22a. Circuito rectificador de media onda con un capacitor en paralelo a una carga resistiva
vo
Vm
V m – Vγ
Diodo apagado. Capacitor
descargándose
A
B
C
Vrizo
Diodo conduciendo.
Capacitor cargándose
t
-Vm
Fig. 2.22b. Voltaje en la carga para el rectificador de media onda de la figura 2.20
La finalidad del capacitor de la figura 2.22a es proporcionar corriente a la carga durante aquellos intervalos en que
el diodo tiene polarización inversa. El capacitor se vuelve a cargar durante los intervalos en los cuales el diodo
conduce. En la figura 2.22b se muestran la señales de entrada y salida aplicadas al circuito de la figura 2.22a;
durante el primer cuarto de ciclo de la señal senoidal, el diodo estará polarizado en directo y el capacitor se cargará
con una constante de tiempo dada por la resistencia del diodo, que típicamente es tan corta que la carga del
16
capacitor puede considerarse como instantánea. Cuando el voltaje de entrada llega a su valor pico Vm, el capacitor
estará cargado al valor pico del voltaje de entrada menos el voltaje umbral del diodo Vγ. Durante la porción negativa
de la señal de entrada, el capacitor no se carga a través del diodo, ya que este está polarizado en inverso, pero si se
descarga a través de la carga, proporcionándole corriente; la constante de tiempo de descarga generalmente es
mucho mayor que la de carga, por lo que la señal de salida tiene la forma de la línea continua presentada en la figura
2.22b. La diferencia entre los valores máximo y mínimo de voltaje a la salida se llama voltaje de rizo. En una fuente
de alimentación bien diseñada, el capacitor será lo suficientemente grande para que entre los períodos de recarga su
voltaje baje en forma mínima hacia la carga, y el voltaje visto por la carga se conserve aproximadamente constante.
Si la carga es una resistencia de valor RL, en el intervalo durante el capacitor se descarga, el diodo estará en
polarización inversa y el capacitor quedará aislado de todo, excepto de la carga. Si hacemos coincidir el eje del
tiempo con el inicio del ciclo de descarga del capacitor, la reducción de voltaje del capacitor puede quedar descrita
mediante la siguiente ecuación.
− t / R LC
(2.8)
vC (t ) = (Vm − Vγ )e
Conforme el tiempo avanza, el voltaje del capacitor sigue reduciéndose, hasta que vi(t) pueda otra vez aplicar
polarización directa al diodo. Esta transición ocurre en el punto B de la figura 2.22, y el capacitor se vuelve a cargar
hasta Vm – Vγ .
La diferencia entre el voltaje de descarga del capacitor y la forma de onda de entrada rectificada (punto A de la
figura 2.22b) no ocurre exactamente en el pico vi. El punto exacto lo podemos calcular tomando en cuenta que
dv
v
(2.9)
i D = iC + i L = C L + L
RL
dt
si hacemos coincidir el eje de tiempo con el punto A, la ecuación 2.9 se convierte
d (Vm cos wt − Vγ ) Vm cos wt − Vγ
V cos wt Vγ
+
= − wCVm sen wt + m
−
(2.10)
iD = C
dt
RL
RL
RL
pero normalmente para circuitos de fuente de alimentación, Vm>>Vγ , por lo que podemos despreciar el último
término. Si resolvemos esta ecuación para iD = 0 (que corresponde al momento donde comienza la descarga),
tenemos que
 1 

tan −1 
wR L C 
1

⇒ t1 =
(2.11)
tan( wt1 ) =
wR L C
w
por ejemplo, para RL = 200 Ω, w = 120π rad y C = 1000 µF, tenemos que t1 = 35.2 µs. Si tomamos en cuenta que el
período de la señal usada es de 16.7 ms, t1 solo representa el 0.21% del período de la señal.
Circuito demodulador AM
En una transmisión de radio AM la amplitud de la onda de alta frecuencia (portadora) varía de acuerdo con la
información de audio que se transmite. Este proceso se denomina amplitud modulada. Puede verse una onda así
Señal demodulada
Envolvente (información)
Portadora de alta frecuencia
Fig. 2.23. Onda modulada en amplitud y señal de audio detectada
17
modulada en la figura 2.23. La información de audio está contenida en la envolvente (el lugar geométrico de los
valores de pico) de la onda modulada. El proceso de extracción de la señal de audio se denomina demodulación.
Con un rectificador de media onda como el de la figura 2.22 y usando la señal modulada como entrada, la salida
es la curva señalada con trazo más grueso en la figura 2.24, bajo el supuesto que la constante de tiempo se haya
escogido adecuadamente, o sea, RLC debe ser bastante pequeña para que, cuando la envolvente decrezca en
amplitud, la diferencia de potencia entre los extremos de C disminuya con suficiente rapidez para seguir a la
envolvente, pero lo suficientemente grande para no introducir excesivo rizado.
Rectificadores de onda completa
Una forma de dividir a la mitad el rizo de una fuente de alimentación, sin aumentar su capacitancia, involucra el
uso de la rectificación de onda completa, de tal forma que se pueda utilizar también la porción negativa de la señal
de entrada para recargar el capacitor.
En el rectificador de onda completa con derivación central, el circuito es alimentado por el embobinado de un
transformador, como en la figura 2.24 b). Cada mitad del secundario con derivación central es responsable de
alimentar uno de los diodos rectificadores. El diodo D1 se pone en polarización directa y carga al capacitor durante
la mitad positiva del ciclo de voltaje de entrada, mientras el dido D2 lo hace durante la parte negativa del ciclo.
Advierta que la polaridad de ambos embobinados secundarios está en la misma dirección. En una fuente con
rectificador de onda completa, el capacitor es recargado durante las porciones tanto positiva como negativa del
ciclo, por lo tanto el capacitor reduce su voltaje aproximadamente sólo durante la mitad del período de la señal. El
voltaje de rizo tiene aproximadamente la mitad del rizo de una fuente de media onda para la misma corriente de
carga y la misma frecuencia de voltaje de entrada.
Otra forma de lograr la rectificación de onda completa es mediante el puente rectificador, que se muestra en la
figura 2.24 c). Durante el semiciclo positivo de la señal de entrada, los diodos D1 y D4 conducen y los diodos D2 y
D3 actúan como circuitos abiertos. Durante el semiciclo negativo, se invierte la situación y son los diodos D2 y D3
los que conducen, estando inactivos D1 y D4. Note que no importa que pareja de diodos conduzca,la polaridad del
voltaje de salida siempre es positiva según está definida en la figura.
Fuente de alimentación con carga no resistiva
En la mayor parte de las aplicaciones electrónicas, la carga no es un resistor simple. Lo más probable es que se
trate de un circuito o una red electrónica compleja, que imponga sobre las terminales de la fuente de alimentación
un conjunto de condiciones de carga que varían con el tiempo, sin embargo, son aplicables los mismos principios
básicos. La corriente utilizada por muchos circuitos electrónicos es una función del tiempo que varían lentamente,
En estas condiciones, la corriente de carga puede considerarse como constante durante varios ciclos de vi. Cuando la
corriente de carga es constante, se puede deducir el descenso de voltaje el capacitor durante su intervalo de descarga
directamente de la relación v/i del capacitor
dv desc arg a (t ) i L
=
(2.12)
dt
C
donde iL es la corriente en la carga y vC(t) es el voltaje en el capacitor. Luego, el voltaje del capacitor en función del
tiempo está dado por
i
(2.13)
vC (t ) = Vmax − v descaga (t ) = Vmax − L t
C
donde Vmax es el voltaje pico de carga del capacitor. Por lo tanto, la reducción del voltaje en el capacitor, que nos dá
el voltaje de rizo, está dada por
i
(2.14)
= L ∆T
Vrizo = v desc arg a
t = ∆T
C
donde ∆T es el período de la señal de entrada para un rectificador de media onda, y el período medio para un
rectificador de onda completa.
D
+
+
vlinea
vi
-
-
vo
+
RL
vo
-
a)
RL
R L + rd
+
+
vi
+
vi
-
vlinea
-
RL
D2
+
vlinea
vi
-
-
D3
D4
b)
-Vγ
+
RL
vi
Vγ
RL
R L + 2rd
D1
D2
RL
R L + rd
vo
vo
-
+
vi
Vγ
D1
+
18
RL
R L + rd
RL
R L + 2rd
vo
vo
-
-2Vγ
c)
vi
2Vγ
Fig. 2.24. Rectificadores de a) media onda b) onda completa con derivación
central c) onda completa con puente rectificador
Ejemplo: Diseñe una fuente de alimentación con un regulador zener y un puente rectificador, que proporcione 10 V
de salida y una corriente de 50 mA a la carga. Asuma que en el puente rectificador se utilizan diodos ideales (rd = rz
= 0) con Vγ = 0.6 V.
Solución
En primer lugar, podemos establecer que el diodo zener debe ser tal que su tensión zener VZ = 10 V, ya que este es
el voltaje que se va a regular, usando el circuito de la figura 2.25. La corriente mínima de regulación de los zener
rara vez es mayor a 1 mA, por lo que podemos tomar este valor; si se desean valores más exactos, se puede recurrir
a los datos proporcionados por los fabricantes. Despreciaremos la resistencia dinámica del zener. La relación del
transformador se determina tomando en cuenta el voltaje pico necesario en el secundario para obtener el voltaje pico
al que se carga el capacitor. El voltaje en el capacitor está dado por los 10V de salida más la caida de tensión a
través de R1 , por lo que es conveniente en primer instancia darle un valor algo mayor a 10V; si Vγ = 0.6 V, entonces
I1
+
120 Vrms
60 Hz
-
+
vi
-
iL
R1
n:1
C1
+
+
vC
VZ
-
-
+
IZ
Carga
vL
-
Fig. 2.25. Fuente de alimentación con puente rectificador y regulador zener
19
120
2 = 17 V y el voltaje pico en C será Vmax = V p − 2Vγ = 15.8 V ,
10
sabemos que I 1 = I L + I Z = I Lmax + I Zmin = I Lmin + I Zmax ya que cuando la carga exija la máxima corriente, la
corriente en el diodo debe ser mayor o igual que la corriente IZmin, de tal forma que continue regulando aún en esa
situación. Cuando la corriente en la carga sea mínima, el diodo zener debe ser capaz de drenar una corriente IZmax.
Entonces
I 1 = I Lmax + I Zmin = (50 + 1) mA = 51 mA
una vez que tengamos la corriente I1, como conocemos la caida de tensión en R1, podemos hallar su valor
− V Z 15.8 − 10
V
=
≈ 114 Ω
R 1 = max
51
I1
pero este no es un valor comercial de resistor, asi que debemos aproximar nuestro resultado, pero siendo cuidadosos
de cumplir aún con los requerimientos cuando hagamos la aproximación. Sea R1 = 120 Ω, entonces
15.8 − 10
= 48.33 mA
I1 =
120
valor que está por debajo de la corriente necesaria. Hemos aproximado por arriba el valor de R1, de 114 a 120 Ω,
limitando asi la corriente a un valor por debajo del especificado. Eso significa que debemos aproximar R1 a un valor
por debajo de 114 Ω. Sea R1 = 110 Ω, entonces
15.8 − 10
= 52.72 mA
I1 =
110
que es mayor a 51 mA.
En el circuito de la figura 2.25 ya tenemos especificados el valor de R1 y VZ. Nos queda por especificar la potencia
que soportan el zener y R1, asi como el valor de C. Calculemos la potencia máxima en el zener
n = 10 ⇒ V p =
I Zmax = I 1 − I Lmin = 52.72 − 0 = 52.72 mA
Luego, la potencia máxima disipada por el zener será
PZ = VZ I Zmax = 10 x52.72 = 0.5272 W
y la potencia disipada en R1
PR1 = I 1 ' ' (Vmax − VZ ) = 305.78 mW
Calculemos C en función del rizo. Sabemos que
dv
1
1
iC = C C ⇒ vC = ∫∆T iC dt = ∫∆T − I 1dt
dt
C
C
I1
si I1 es constante, entonces vC = − ∆T . Como usamos un rectificador de onda completa, ∆T = T/2; luego,
C
I1 T
, lo que significa que hay una reducción de ese valor durante la descarga, por lo tanto, el voltaje de rizo
vC = −
C 2
está dado por esa caida y
IT
C= 1
2Vrizo
Hasta ahora hemos asumido que I1 es constante, sin embargo, sabemos que, a pesar que la regulación por zener
nos permite drenar la corriente que no utilice la carga, esta aún es función del voltaje en el condensador, y que este
baja hasta un valor mínimo vCmin, lo que provoca el voltaje de rizo. Podemos calcular el rizo máximo permitido de
tal forma que I1 nunca sea menor a 51 mA. Luego
vCmin − 10
= 51 ⇒ vCmin = 15.61 = Vmax − Vrizo ⇒ Vrizo = 0.19 V
R1
que representa el voltaje de rizo máximo permitido. Entonces
C=
sea C = 2.4 mF, entonces, el rizo será
(51 mA) x(16.7 ms)
= 2.2413 mF
2 x0.19 V
20
Vrizo =
(51 mA) x(16.7 ms)
= 177.44 mV
2 x 2.4 mF
y la corriente por R1 será
I1 =
v min − 10 Vmax − Vrizo − 10
=
= 51.1 mA
110
110
o, para ser más exactos, podemos resolver el siguiente sistema de ecuaciones:
y el resultado es:
Vmax − Vrizo − 10

 I 1 =
V − Vo
R1
⇒ Vrizo = max

2CR1
V = I 1 T
+1
rizo
T
C 2

Vrizo = 177.8 mV
e
I 1 = 51.11 mA .
Resultado
Capacitor C = 2.4 mF
Zener con VZ = 10 V y con capacidad de disipar hasta 1 W de potencia
Resistor de 110 Ω y con capacidad de disipar hasta 0.5 W de potencia
Si tomamos en cuenta que la tolerancia de la resistencia podria generar una situación en que la corriente I1 esté
por debajo de los 51 mA especificados. Si la tolerancia de R1 es de ±5%, vemos que R1 puede tomar valores desde
R1’’ = R1(0.95) = 104.5 Ω. Si R1’ = 115.5 Ω,
R1’ = R1(1.05) = 115.5 hasta
15.8 − 10
= 50.22 mA < 51 mA
I1 ' =
115.5
por lo tanto, el valor de 110 Ω con una tolerancia de ±5% no nos sirve. Sea R1 = 100 Ω.
Entonces
y
R 1 ' = R 11.05 = 105 Ω; R 1 ' ' = R 1 0.95 = 95 Ω
15.8 − 10
15.8 − 10
= 55.52 mA > 51 mA; I 1 ' ' =
= 61.05 mA > 51 mA
I1 ' =
105
95
luego, en el peor de los casos, en que R1 = 105 Ω, la corriente que circula por esa resistencia será mayor a la
necesaria para suministrar 50 mA a la carga y mantener al zener regulando.
En el circuito de la figura 2.25 ya tenemos especificados los valores de R1 y su tolerancia, así como VZ. Nos queda
por especificar la potencia que soportan el zener y R1, asi como el valor de C. Calculemos la potencia máxima en el
zener
I Zmax = I 1 ' '− I Lmin = 61.05 − 0 = 61.05 mA
hemos tomado el valor de I1’’ por representar el peor de los casos. Luego, la potencia máxima disipada por el zener
será
PZ = V Z I Zmax = 10 x61.05 = 0.61 W
y la potencia disipada en R1
PR1 = I 1 ' ' (Vmax − VZ ) = 0.354 W
Calculemos C en función del rizo. Sabemos que
dv
1
iC = C C ⇒ v C =
dt
C
1
∫∆T iC dt = C ∫∆T − I1dt
21
si I1 es constante, entonces vC = −
I1
∆T . Como usamos un rectificador de onda completa, ∆T = T/2; luego,
C
I1 T
, lo que significa que hay una reducción de ese valor durante la descarga, por lo tanto, el voltaje de rizo
C 2
está dado por esa caida y
IT
C= 1
2Vrizo
Hasta ahora hemos asumido que I1 es constante, sin embargo, sabemos que, a pesar que la regulación por zener
nos permite drenar la corriente que no utilice la carga, esta aún es función del voltaje en el condensador, y que este
baja hasta un valor mínimo vCmin, lo que provoca el voltaje de rizo. Podemos calcular el rizo máximo permitido de
tal forma que I1 nunca sea menor a 51 mA. Luego
vCmin − 10
= 51 ⇒ vCmin = 15.355 = Vmax − Vrizo ⇒ Vrizo = 0.445 V
R1 '
que representa el voltaje de rizo máximo permitido. Si establecemos que Vrizo = 0.4 V, entonces
(51 mA) x(16.7 ms)
= 1.0625 mF
C=
2 x0.4 V
sea C = 1.2 mF, entonces, el rizo será
(51 mA) x(16.7 ms)
= .3542 V
Vrizo =
2 x1.2 mF
y la corriente por R1 será
v
− 10 Vmax − Vrizo − 10
=
= 51.9 mA
I 1 ' = min
105
105
Note que asumimos que la corriente I1 era constante para calcula la capacitancia, pero como el rizo causa una
variación en esta corriente, nuestro calculo es aproximado. Sin embargo, la diferencia entre el valor de I1 usado para
calcular C y el resultante producto del rizo varia en un 1.73%, por lo que podemos concluir que nuestro calculo es
bastante exacto. Si se requiere un mayor nivel de precisión, se puede iterar sucesivamente en el cálculo de C con el
valor I1’ calculado en función del rizo, o se puede resolver el siguiente sistema de ecuaciones:
vC = −
resultando:
Vmax

 I 1 =

V = I 1
 rizo C
− Vrizo − 10
V − Vo
105
⇒ Vrizo = max
2CR1
T
+1
T
2
Vrizo = 360.5 mV
e
I1 = 51.8 mA .
Resultado
Capacitor C = 1.2 mF
Zener con VZ = 10 V y con capacidad de disipar hasta 1 W de potencia
Resistor de 100 Ω ± 5 % y con capacidad de disipar hasta 0.5 W de potencia
Circuitos conformadores
Algunos circuitos sencillos con diodo útiles para construir circuitos complejos se muestran en el figura 2.26. Al
trabajar con circuitos conformadores nos enfrentamos a los siguientes problemas básicos:
ƒ
Problemas de análisis: Consiste en, dado un circuito, determinar:
P.1) Su característica iS contra vS
P.2) Su característica de transferencia vO contra vS
ƒ
Problemas de síntesis: Consiste en sintetizar un circuito, dada:
22
P.3) Su característica iS contra vS
P.4) Su característica vO contra vS
D1
P.1) Análisis dado un circuito, para determinar iS /vS
Ilustremos el procedimiento mediante un ejemplo.
Hallemos la característica iS /vS del siguiente circuito:
+
iS
1
D2
1
2
5
1
2
23
+
i
i
A
+
1/R
R
v
V
i
-
+
C
i
V
R
+
i
B
V
V
i
D
i
-V
v
V
1/R
1/R
-
i
i
v
-V
R
v
V
-
i
1/R
R
-
+
+
E
i
i
F
I
R
I
R
-
+
i
G
i
I
R
-
v
1/R
I
-I
-
+
1/R
v
1/R
i
i
R
v
I
-
Fig. 2.26. Elementos compuestos
H
I
-I
v
1/R
24
D1
Pasos 1) Identifiquemos las ramas con números.
iS
+
1
2
1
D2
1
1
2
5
3
2
2) Grafiquemos la característica i/v de cada una. En nuestro ejemplo
1
i1
i2
2
1
3
1/2
i3
1
2.5
-2
1
v1
-5
2
v2
v3
-2
2) Sumemos las características i/v de los elementos. Para obtener la característica del sistema constituido por la
combinación de las ramas 2 y 3, debemos tomar en cuenta en que forma están conectadas estas ramas. Vemos que
están en conectadas en paralelo, así que el sistema compuesto por 2 y 3, que llamaremos 23, sería
i23
23
+
D2
i2
2
5
1
i3
2
Com las ramas 2 y 3 están conectadas en paralelo, la corriente i23 resultante de esta combinación será la suma de i2
e i3 , mientras que el voltaje v23 será igual a v2 y v3 . Por lo tanto, la característica i23 /v23 la obtenemos como la suma
en corriente de i2 /v2 e i3 /v3 , o sea, como el voltaje v23 se conserva igual a v2 y v3 , tomamos un valor de tensión y
buscamos las corrientes i2 e i3 correspondiente; la corriente i23 será igual a la de estas corrientes. Veamos como se
aplica esto en nuestro ejemplo.
Para v 23 = −5 : en 2 i 2 = 0
 ⇒ i 23 = −7
en 3 i3 = −7 
Para v 23 = −7 : en 2 i2 = 0 
 ⇒ i 23 = −9
en 3 i3 = −9
Para v 23 = 0 : en 2 i 2 = 2.5
 ⇒ i 23 = 0.5
en 3 i3 = −2 
Hemos obtenido la caracterítica i23 /v23 mediante la adición de corrientes en cada punto, sin embargo, pudimos
obtenerla mediante la suma de las pendientes de las características de 2 y 3 en cada tramo. Por ejemplo
25
Para v 23 < −5 : en 2 m2 = 0
 ⇒ m 23 = m2 + m3 = 1
en 3 m3 = 1 
2
1
Para v 23 > −5 : en 2 m2 = 
3
2  ⇒ m 23 = m2 + m3 =
2
en 3 m3 = 1 
i2
1/2
23
2.5
-7
-7
-5
-5
i23
3/2
0.5
v23
v2
3
i3
⇒ 2 + 3 = 23 ⇒
(i)
1
1
2
-7
-9
v3
-2
-7
-9
Luego, podemos concluir que cuando las ramas están en paralelo sumamos en corriente, lo que significa que
sumamos las corrientes de las características de las ramas para valores dados de voltaje, o sumamos las pendientes
de las características para cada tramo.
Vemos que ahora tenemos que añadir a la rama resultante 23 la rama conectada en serie 1, para obtener la
característica iS /vS .
D1
1
+
i123
1
v
1
2
3
1
23
Al sumar estos elementos debemos tomar en cuenta que están conectados en serie, por lo tanto, ahora es la
variable i123 la que será común a ambas ramas. Por lo tanto tomamos valores de corriente y sumamos las tensiones
v1 y v23 correspondientes.
26
1
Para i = −9 : en 1 v = 0 
 ⇒ v = −7
en 23 v = −7 
Para i = −7 : en 1 v = 0 
 ⇒ v = −5
en 23 v = −5
Para i = 0.5 : en 1 v = 0
⇒v =0
en 23 v = 0 
Para i = 2 : en 1 v = 1 
⇒v =2
en 23 v = 1
i1
123
23
1
i123
3/5
i23
2
2
1
3/2
1
v1
-7
-5
0.5
-7
1/3 1
1
-5
1/3 2 v123
v23
⇒ 23 + 1 = 123 ⇒
(v)
3/2
-7
1
-9
1
Si tomamos las pendientes
Para i123 < −7 : en 1 m1 = ∞ 
1
1
1
=
+
= 1 ⇒ m123 = 1
⇒
en 23 m 23 = 1 m123 m1 m23
Para - 7 < i123 < 1 : en 1 m1 = ∞ 
1
1
1
2
3

=
+
= ⇒ m123 =
3 ⇒
2
en 23 m 23 =  m123 m1 m23 3
2
Para i123 > 1 : en 1 m1 = 1
1
1
1
5
3

=
+
= ⇒ m123 =
3 ⇒
5
en 23 m23 =  m123 m1 m23 3
2
-7
-9
Luego, podemos concluir que cuando las ramas están en serie sumamos en tensión o voltaje, lo que significa que
sumamos los voltajes de las características de las ramas para valores dados de corriente, o sumamos el inverso de
las pendientes de las características para cada tramo, para obtener el inverso de la pendiente en la característica
resultante.
La característica iS /vS es igual a la correspondiente a 123, ya que hemos incluido todas las ramas del circuito.
27
P.2) Análisis dado un circuito, para determinar vo /vS
D1
2
1
iS
+
1
D2
1
2
5
1
3
2
Para resolver este problema se debe determinar el estado de los diodos D1 y D2 y los valores de vS para los cuales
cambian de estado; esto lo podemos hacer mediante suposiciones, procedimiento que hemos descrito anteriormente.
Otra forma de saber cual es el circuito resultante para cada intervalo es utilizando la característica iS/vS del circuito,
característica que obtuvimos cuando resolvimos el problema P.1. La característica que obtuvimos anteriormente es
De la característica iS /vS podemos obtener la siguiente información: Como la pendiente para vS < -5 V es igual a 1,
podemos concluir que D1 conduce y D2 no conduce, ¿porqué?, porque no existe otra combianción de estados para
D1 y D2 que resulte en un circuito que presente una resistencia R = 1. Comprobemos esto ensayando todas las
combinaciones posibles:
– Si D1 off y D2 off, el circuito resultante será
iS
3/5
+
1
iS
-7
1
2
1
+
-5
1/3 2 vS
1
3/2
2
-7
-9
1
La pendiente de la característica iS /vS para este circuito es ½, y no corresponde a ninguno de los tramos de la
característica iS /vS que obtuvimos, asi que este estado no es posible.
– Si D1 on y D2 off, el circuito resultante será
+
iS
+
1
2
La pendiente de la característica iS /vS para este circuito es 1, y podemos
observar que pertence al primer tramo, asi que podemos concluir que este
estado se presenta para vS < -7 V.
28
– Si D1 off y D2 on, el circuito resultante será
+
iS
1
+
La pendiente de la característica iS /vS para este circuito es
1
2
1
5
2
−1
1
3
1 
m −1 =  + 1 + ⇒ m = , y podemos observar que
2
1
5


pertence al tercer tramo, asi que podemos concluir que este
estado se presenta para vS > 2 V.
– Si D1 on y D2 on, el circuito resultante será
La pendiente de la característica iS /vS para este circuito es
iS
1
3
+
+
m = + 1 ⇒ m = , y podemos observar que pertence al segundo tramo,
2
2
asi que podemos concluir que este estado se presenta para –7 < vS < 2 V.
1
2
5
2
Entonces podemos notar que podemos conocer los estados de los diodos, y por lo tanto la constitución del
circuito, por intervalos, observando la característica iS /vS . Para identificar los estados de los diodos, debemos hallar
la combinación de resistencias en el circuito que nos dé una pendiente como la del intervalo. En circuitos sencillos
como el utilizado en este ejemplo, es posible considerar todas la opciones posibles, pero si aumenta el número de
diodos, aumenta también el número de posibilidades, llegando a ser prohibitivo explorarlas todas; por ejemplo, para
un circuito con sólo cuatro diodos, tenemos 42 = 16 posibilidades, o sea, 16 posibles circuitos, sin embargo,
generalmente la característica iS /vS tendrá sólo cinco tramos. Si podemos deducir los estados de los diodos a partir
de la característica iS /vS , nos ahorraremos el tiempo invertido en considerar nueve estados que no son posibles.
Hasta ahora hemos ido desde los circuitos posibles a la característica iS /vS , sin embargo, lo que deseamos es
conocer los estados a partir de la característica iS /vS , o sea, el proceso inverso. Consideremos la característica iS /vS
que reproducimos a continuación. En el tramo 1 m = 1, asi que debemos hallar una combinación de resistencias que
nos dé esa pendiente. Examinando el circuito vemos que la rama 3 siempre está activa, por lo tanto esa pendiente
sólo es posible si D1 está en corto circuito y D2 abierto, o sea, D1 on y D2 off. Por lo tanto el circuito equivalente
es
iS
iS
3/5
+
+
2
3
1
1
-7
-5
y vo = vS para vS < -5 V
1/3 2 vS
2
2
3/2
1
-7
-9
1
29
En el tramo 2 m = 3/2, lo que es posible si tanto D1 como D2 están en corto circuito, o sea, D1 on y D2 on. Por lo
tanto el circuito equivalente es
+
1
iS
1
y vo = vS para –5 < vS < 1/3 V
+
2
1
5
2
En el tramo 3 m = 3/5, lo que es posible si D1 está abierto y D2 está en corto circuito, o sea, D1 off y D2 on. Por
lo tanto el circuito equivalente es
iS
2
5 2
1
+
+
y v o =  i S + 2 −  =  i S −  , pero
2 3
2
3
1 
1 3
4
iS =
 v S + 1 +  =  v S +  , luego
1
2
2
3 5 
3
1+ 
3
5
23
4 1 2
4 1 2
1
v o =   v S +  −  =  v S +  − =  v S + 
2
35
3 2 5
3 3 5
2
para vS > 1/3 V
Luego, la característica vo/vS será como se muestra en la siguiente gráfica
vo
2/5
-7
1/3
1/3
vS
1
-7
P.3) Síntesis de un circuito a partir de su característica iS /vS
Para resolver este problema debemos considerar lo siguiente:
a) Para obtener una característica i/v con N puntos singulares se requiere
un circuito con N diodos. Por ejemplo, considere el circuito que hemos
analizado
iS
-7
3/5
2
1
-5
1/3 2
Puntos
singulares
3/2
-7
-9
1
vS
30
D1
1
iS
+
D2
1
1
2
5
2
b) Al agregar un elemento en serie a la entrada de un circuito, la pendiente de la característica i/v disminuye en
algunos tramos, dejando otros sin modificación. Los tramos que no sufren alteración son aquellos en que el
elemento añadido tiene un valor constante de tensión, o sea, que se pueden representar como una fuente de tensión
o un corto circuito. Por ejemplo
D1
i23
D1
+
1
iS
D2
+
i1
D2
1
1
+
=
2
(serie)
1
1
i2
i3
2
5
1
2
5
+
v1
2
i1
i23
-7
-5
v23
+
(v)
1
v1
=
Tramo
inalterado
-7 -5
-9
2
1
Tramo
alterado
1/3 2
3/2
-7
1
3/5
1
-2
3/2
0.5
iS
Tramo
inalterado
vS
-7
-9
1
Al agregar un elemento en paralelo a la entrada de un cirucito, la pendiente de algunos tramos aumenta,
mientras otros queda inalterada. Los tramos inalterados son aquellos en que el elemento añadido se puede
represetar como una fuente de tensión o es un circuito abierto. Por ejemplo
c)
31
+
i23
+
+
D2
1
+
(paralelo)
i3
1
i3
5
2
i23
1/2
i3
2.5
1
+
(i)
=
2
v2
-5
2
i2
5
2
i2
=
2
i2
D2
-7
Tramo
alterado
v23
0.5
-5
3/2
v3
-2
-7
-9
1
Tramo
inalterado
Luego de estas consideraciones, ilustremos el procedimiento para
sintetizar un circuito a partir de su característica i/v a utilizando un
ejemplo. Dada la siguiente característica i/v, hallar un circuito que la
produzca
iS
5
-5
1. Se identifican los segmentos de la característica iS /vS . En este caso
hemos identificados con los números romanos I, II y III.
2. Se identifica la característica i/v del primer tramo y se busca un
elemento que la produzca. En nuestro ejemplo podemos escoger
1/2
III
II
1
I
5
vS
-5
1/2
i
+
-5
5
-2.5
I
v
≡
2
i
-5
1/2
-
5
3. Se busca un elemento que modifique la característica i/v de I para obtener II. En nuestro caso debemos dejar
invariante I antes de (-5,-5) y aumentar la pendiente a partir de este punto en ½. Por lo tanto, debemos colocar un
elemento en paralelo que tenga una resistencia de 2 y actúe a partir de –5V.
32
D1
i
i
1
5
+
5
v
≡
1
v
i
+
D
v
i
1/2
≡
2
2.5
5
-
-5
v
y el circuito resultante es
i
5
i
II
+
D
v
-5
2
2
5
≡
5
-
5
I
v
-5
1/2
4. Se busca ahora un elemento que modifique II a III, o sea, que reduzca la pendiente a ½. Como hay una reducción
de pendiente, el elemento a añadir debe estar en serie, y debe tener una resistencia tal que
−1
1 1 1 
1
=  +  ⇒ 2 = 1 + ⇒ m = 1 . Luego, debemos añadir un elemento en serie que contenga una resistencia de
2 1 m 
m
valor 1 y que actúe a partir de (5,5). Como la suma es en tensión y queremos dejar inalterado II antes de (5,5), el
nuevo elemento debe tener una tensión v = 0 para i < 5, y a partir de ahí una pendiente de 1. Luego
i
D1
i
1
+
5
v
≡
5
1
v
-
33
5. El circuito resultante es
iS
+
iS
vS
1
1/2
5
5
2
-
-5
≡
2
III
II
1
5
I
5
5
vS
-5
1/2
Problema tipo.
– Sabiendo que V1 = V2 = 20 V , V3 = V4 = 5 V y que cada diodo presenta un rd = 0 y Vγ = 0.7 V.
a) Determine el valor de Vo
b) Determine el valor de la corriente para cada diodo
V1
D1
D3
D5
Vo
D4
V2
D2
20 kΩ
5 kΩ
D6
V3
V4
5 kΩ
25 V
Solución
Sabemos que el estado de D1 y D2 es el mismo, ya que V1 = V2, igualmente, el estado de D5 es el mismo que D6.
Luego, podemos obviar una de las ramas, tomando en cuenta que la corriente se divide entre ambas. Luego,
podemos dibujar el circuito de la siguiente forma:
20 V
ID12
ID3
D1
D3
Vo
ID4
ID56
D4
20 kΩ
D6
5 kΩ
5V
5 kΩ
25 V
Donde ID12 = ID1 + ID2
ID56 = ID5 + ID6
Supongamos que D1, D4 y D6 conducen y D3 no conduce. Sustituyendo los diodos qur conducen por su modelo
equivalente, tenemos que
34
ID12
20 V
Vγ
V’’ ID3
Vo
- vD3 +
ID4
V’
ID56
Vγ
Vγ
20 kΩ
5 kΩ
5V
5 kΩ
25 V
Luego Vo = 25 − 20 I D 4 , pero Vo = 5 − Vγ + Vγ = 5 V , entonces I D 4 =
25 − 5
= 1 mA . Como ID4 > 0, D4 conduce,
20
com habiamos supuesto.
4.3
− I D 4 = −0.14 mA . Por lo tanto, D5 y D6 no
5
conducen, contradiciendo nuestra suposición. Ahora debemos suponer otra combinación de estados.
Supongamos que D1 y D4 conducen y D3 y D5 no conducen. El circuito equivalente es
Sin embargo, V ' = 5( I D56 + I D 4 ) = 5 − 0.7 = 4.3 ⇒ I D 56 =
ID12
20 V
Vγ
V’’ ID3
- vD3 +
Vo
ID4
Vγ
20 kΩ
5 kΩ
V’
ID56
- vD5 +
5V
5 kΩ
25 V
V ' ' 20 − 0.7
=
= 3.86 mA , por lo tanto, D1 y D2 conducen.
5
5
25 − 0.7
= 0.972 mA , y por lo tanto, D4 conduce.
Vo = 25 − 20 I D 4 = 0.7 + V ' = 0.7 + 5 I D 4 ⇒ I D 4 =
25
V '+V D5 − 5 = 0 ⇒ V D5 = 5 − V ' = 5 − 5 I D 4 = 0.14 V , y como supusimos, D5 no conduce.
I D12 =
Vo = 25 − 20 I D 4 = 5.56 V , V D3 = Vo − V ' ' = 5.56 − 5 I D12 = 5.56 − 19.3 = −13.74V , por lo tanto, D3 no conduce
Hemos comprobado que nuestra hipótesis era válida, así que procedemos a calcular la corriente en cada diodo.
I
I D1 = I D 2 = D12 = 1.93 mA , I D5 = I D 6 = I D3 = 0 , I D 4 = 0.972 mA
2
Respuesta: Vo = 5.56V , I D1 = 1.93 mA , I D 2 = 1.93 mA , I D3 = 0 I D 4 = 0.972 mA , I D5 = 0 , I D 6 = 0 .
35
CIRCUITOS CON DISPOSITIVOS DE TRES TERMINALES
Introducción
Es posible describir un dispositivo de tres terminales considerando sólo dos de ellos, tomando un terminal como
común.
Puerto 3
i1
i2
+
v2
-
+
v1
-
Puerto 1
Puerto 2
Fig. 3.1. Dispositivo de tres terminales, modelado con dos de sus puertos
En general, un puerto funciona como puerto de entrada o de control, y el otro como puerto de salida o controlado.
Por ejemplo, el MOSFET canal n en configuración surtidor común tiene como puerto de entrada el puerto puertasurtidor (G-S), y como salida el puerto drenador-surtidor (D-S), siendo un dispositivo controlado por voltaje. Su
característica i/v de salida es
iD (mA)
D
iD
iG
G
+
vDS
-
+
vGS
-
a)
vGS = 6V
20
vGS = 5V
vGS = 4V
10
vGS = 3V
vGS = 2V
S
vDS (V)
b)
Fig. 3.2. a) símbolo de un MOSFET-n. b) característica i/v del puerto de salida
mientras que el BJT es un dispositivo controlado por corriente, y su característica i/v de salida es
iC (mA)
iB = 60 µA
C
iC
B
iB
+
vCE
-
+
vBE a)
20
iB = 50 µA
iB = 40 µA
10
iB = 30 µA
iB = 20 µA
E
b)
Fig. 3.3. a) símbolo de un BJT npn. b) característica i/v del puerto de salida
vCE (V)
36
Modelo del BJT para bajas frecuencias
Como la característica i/v del puerto de entrada del BJT se parece a la de un diodo de unión pn, podemos
modelarla mediante segmentos lineales usando una resistencia rbe y una fuente de voltaje Vγ. Como
I
di
i
1
= B
= ES e vBE / ηFVT
≅ B
i B = I ES (e vBE / ηFVT − 1) ⇒
i
I
=
η F VT
η F VT i = I
rb'e dv BE B BQ
v =V
v BE =VBEQ
rb 'e =
luego,
η F VT
iB
=
iB = I BQ
BE
BEQ
B
BQ
η F VT
.
IB
(3.1)
Tomemos en cuenta que la corriente total de base iB es tal que iB = IB + ib, donde IB es la corriente de polarización
de base e ib es la corriente de pequeña senal de base. Por lo tanto, debemos modelar el dispositivo para cada región
como constituido por elementos de polarización y elementos de pequeña señal, que combinados forman el modelo
completo del dispositivo.
Para modelar el puerto de salida, consideremos primero el componente de polarización. Supondremos que las
curvas i/v de salida son horizontales en la región activa (región de corriente constante). Luego, i/v es una línea
horizontal cuya altura depende de iB, o sea, IC = β FIB; por lo tanto, podemos modelar al dispositivo en esta región
como una fuente de corriente de valor β FIB. Una vez polarizado el dispositivo, una fuente de pequeña señal produce
variaciones de iC tales que ∆ iC = β o ∆iB ⇒ ic = β o ib. Notese que hemos distinguido entre β F y β o. La primera
representa la ganancia de corriente de gran señal, y se aplica al componente de polarización, mientras que la última
se refiere a la ganancia de corriente incremental o de pequeña señal, y se define como
∂i
i
(3.2)
βο ≡ C
= c
∂i B iC = ICQ
ib
vCE =VCEQ
El factor βo expresa los cambios incrementales en iC que resultan del desplazamiento ib a partir de IB .
iC (mA)
∆iC = ic = βo ib
Q
IC = βF IB
vCE (V)
Fig. 3.4. Representación gráfica de diferencia entre βF y βo
Si iC contiene componentes tanto de polarización (IC) como de pequeña señal (ic), el modelo resultante es
37
B iB
+
+
vbe
-
vBE
Componentes
de señal
B’
rx
iC
C
+
rb’e = rπ
IC = β F IB
ic = β o ib
rce
vCE
Vγ
E
iE
Componentes de
polarización
E -
Fig. 3.5. Modelo del BJT en la región activa
Resistencia en pequeña señal del puerto de salida
La modulación del ancho de la base del BJT ocasiona una inclinación de las curvas i/v de salida en la región de
corriente constante (efecto Early). Este efecto puede representarse en el modelo de segmentos lineales del
dispositivo agregando una resistencia en paralelo con las fuentes de corriente
∂v
V + VCE
V
,
(3.3)
= A = A
rce = CE
∂iC iC = IC
iC (0)
IC
vCE =VCE
los valores típicos de rce para el BJT están alrededor de los 100 kΩ.
1/rce
iC (mA)
(IC , VCE)
iC (0)
-VA
vCE (V)
Fig. 3.6.Interpretación gráfica del voltaje Early y la resistencia de salida
Modelo de transconductancia del BJT
Se puede utilizar un modelo alternativo para el BJT, donde la corriente de pequeña señal del colector está
controlada por la caida de tensión vbe a través de rbe . La estructura de este modelo se presenta en la figura 3.7. Note
que la única diferencia respecto al modelo de la figura 3.5 está en la fuente de corriente que representa la corriente
de colector de pequeña señal. La transconductancia gm se define como
∂i
∂i ∂vb 'e
∂i
∂i
∂i
v
⇒ g m vb'e = C vb 'e = C ib rb 'e = C
gm = C
ib = C ib = β o ib ⇒ β o = g m b'e = g m rb 'e y
∂vb 'e I ,V
∂vb'e
∂vb'e
∂vb 'e ∂ib
∂ib
ib
C
CE
finalmente
gm =
βo
rb 'e
(3.4)
38
Componentes
de señal
B’
rx
B iB
iC
+
+
vbe
-
vBE
C
+
rb’e = rπ
IC = β F IB
rce
ic = β o ib
vCE
Vγ
E
iE
Componentes de
polarización
E -
Fig. 3.7. Modelo de transconductancia del BJT en la región activa
Resistencia en pequeña señal del puerto de entrada del BJT
La resistencia en pequeña señal del puerto de entrada del BJT (rx) toma en cuenta los efectos de cualquier
resisitencia ohmica que pudiera aparecer en serie con el terminal de entrada, debida a los contactos físicos y a la
trayectoria de conducción transversal en la región de base. rx representa una resistencia física real y no una
resistencia derivada de una pendiente o de una característica i/v. Para un dispositivo dado, el valor de rx puede
medirse o estimarse, dependiendo su valor de las técnicas de fabricación del dispositivo. En la literatura
generalmente se llama hie a la suma de rx y rb’e; sin embargo, rb’e es generalmente mucho mayor que rx, y por lo tanto
para corrientes moderadas de base se puede despreciar este valor. Sin embargo, rx es la que limita la corriente en la
unión base emisor para polarización directa elevada, por lo que debe considerarse cuando la corriente de base
alcance valores del orden de las decenas de mA.
Modelo del BJT considerando regiones distintas a la activa
Los modelos de las figura 3.5 y 3.7 no consideran regiones distintas a la región activa, y por lo tanto son válidos
solo cuando el transistor opere en ella. Para considerar las regiones de corte y saturación, debemos agregar
elementos a la entrada y a la salida de los modelos. Consideremos solamente las modificaciones en el modelo de la
figura 3.5, tomando en cuenta que las mismas se aplican al modelo de conductancias de la figura 3.7.
Para incluir la operación en corte, debemos colocar un diodo ideal a la entrada, de tal forma que mientras no se
supere el voltaje umbral Vγ , la corriente de base sea nula, al igual que la corriente de colector. Para tomar en cuenta
la región de saturación, debemos considerar que en esta región la tensión colector emisor es practicamente constante
e igual a un valor VCE(sat) . En serie a una fuente que represente este valor, debemos colocar un diodo que conduzca
sólo cuando la tensión colector emisor caiga bajo VCE(sat) . Hasta ahora se ha omitido la corriente inversa de
saturación ICO , corriente que puede despreciarse sin mucho error a temperatura ambient, pero puede llegar a ser
significativa a altas temperaturas. El modelo completo quedaría como se ilustra en la figura 3.8.
B
+
vBE
E
iB
B’
rx
+
vbe
-
iC
rb’e = rπ
Vγ
C +
vCE
rce
β F IB
(β F +1) ICO
ic = βoib
VCE (sat)
iE
E
-
Fig. 3.8. Modelo de del BJT considerando las regiones activa, de corte y de saturación
En función de las regiones de funcionamiento que podemos diferenciar en el BJT, podemos concluir que la
corriente de colector estará dada por las siguiente expresiones
39
Región de corte
0
∀ v BE < Vγ

Región de saturación

iC = cualquier valor
∀ v BE > Vγ ∧ vCE = VCE ( sat )

Región de corriente constante o saturación

vCE
∀ v BE > Vγ ∧ vCE > VCE ( sat )
 β F I B + β o ib + ( β F + 1) I co +

rce
(3.5)
Dependencia de los BJTs de la temperatura
Al variar la temperatura a la que operan estos dispositivos, esperamos una variación de su punto de
funcionamiento. Sabemos que la tensión umbral del dispositivo disminuye 2.5 mV por ºC, o sea
∆Vγ ≈ −(2.5 mV/º C)∆T .
La corriente inversa de saturación de las uniones pn aumenta con la temperatura, duplicandose aproximadamente
por cada diez ºC
T2 −T1
I CO (T2 ) = I CO (T1 ) x 2 10 .
La variación de β es una relación compleja, generalmente incremental con la temperatura. Generalmente se describe
en forma gráfica.
Transistores de efecto de campo (FETs)
MOSFET incremental o de enriquecimiento
Debido a la capa de óxido conectada al terminal de puerta, la corriente de puerta es
cero o muy pequeña. La corriente no puede fluir de drenaje a fuente a menos que vGS
sea mayor que un voltaje umbral VTR , que es un parámetro fijo para cada dispositivo
y es positivo para un canal MOSFET incremental canal n. La cantidad que vGS exceda
a VTR se llama voltaje excedente de compuerta. El MOSFET “se encenderá” cuando
se aplique un voltaje excedente de compuerta mayor que cero. En la característica i/v G
de salida del dispositivo pueden diferenciarse tres regiones de operación: 1) Una
región de corte, donde el voltaje excedente de compuerta es menor que cero 2) una
región resistiva o triodo (llamada así por su similitud con el triodo de vacío),
correspondiente a la parte no lineal de las curvas y 3) una región de corriente
constante, correspondiente a la porción plana o casi plana de la característica i/v de
salida.
Región de corte
0
∀ vGS < VTR

Región triodo o resistiva

iD = 
2
 K 2(vGS − VTR )v DS − v DS ∀ vGS > VTR ∧ 0 < v DS < vGS − VTR
Región de corriente constante o saturación

 K (vGS − VTR ) 2
∀ vGS > VTR ∧ v DS > vGS − VTR
[
]
D
iD
iG
+
vGS
+
vDS
-
S
(3.6)
40
Región de corriente
constante
Región triodo
iD (mA)
vDS = vGS - VTR
vGS = 5V
vGS = 4V
vGS = 3V
vGS = 2V
Región de corte
vDS (V)
Fig. 3.9.Regiones de la característica i/v de salida de un MOSFET-n
En la región triodo, iD es función de vGS y vDS , mientras que en la región de corriente constante es sólo función del
voltaje excedente de compuerta. En todas las regiones, iG = 0, pues la compuerta está aislada por medio de una capa
de óxido.
MOSFET decremental o de empobrecimiento
Es un MOSFET con un voltaje umbral de signo contrario al incremental, o sea, si es
canal n, VTR será negativo, y si es canal p, VTR será positivo; en todo caso, el dispositivo
estará fuera del corte aún con un vGS igual a cero. El dispositivo decremental tiene
“construido” un canal conductor entre su drenaje y surtidor. Cuando se aplica un vGS
positivo, se incrementa la conductividad del canal, aumentando iD . Cuando se aplica un
vGS negativo se reduce el valor de iD , pudiendo ser llevado al corte. El dispositivo se
fabrica construyendo un canal entre drenador y surtidor, implantando en el sustrato tipo
p (n) una capa microscópica muy delgada de iones donadores (aceptadores). Esta capa
sirve como canal conductor aún en ausencia de vGS .
D
iG
G
+
vGS
iD
+
vDS
-
-
S
Transistor de efecto de campo de unión (JFET)
El JFET tiene características i/v muy similares a las del MOSFET decremental, y al
igual que este, es un dispositivo controlado mediante la tensión en el puerto de entrada;
sin embargo, los procesos físicos que permiten el funcionamiento del dispositivo son
muy distintos, como hemos estudiado en la primera parte del curso. Como en esta
sección nos encargamos del estudio del comportamiento del dispositivo cuando forma
parte de un circuito, podemos ignorar esas diferencias.
El JFET presenta regiones de corte, triodo y saturación similares a las del MOSFET-n
decremental, pero su voltaje umbral (VTR) es de signo contrario; pero a diferencia del
MOSFET-n decremental, no es posible aplicar un vGS positivo, porque estariamos
polarizando la unión pn de compuerta a canal, y la corriente de compuerta fluirá de la
misma manera que en un diodo en directo.
Región de corte
0
∀ vGS < VTR

Región triodo o resistiva

.
iD = 
2
 K 2(vGS − VTR )v DS − v DS ∀ vGS > VTR ∧ 0 < v DS < vGS − VTR
Región de corriente constante o saturación

 K (vGS − VTR ) 2
∀ vGS > VTR ∧ v DS > vGS − VTR
[
]
D
G
+
vDS
-
iG
+
-
vGS
S
D
G
(3.7)
iD
iG
+
vDS
-
+
vGS
iD
S
41
Algunas veces se especifican la corriente drenadora en corte (IDSS) y la tensión de estricción para un dispositivo
decremental o tensión umbral para un dispositivo incremental (VP). La relación entre los parámetros que ya
conocemos y estos es la siguiente
I
(3.8)
K = DSS2
V P = VTR
VP
y podemos obtener un conjunto de ecuaciones alternas para el JFET
Región de corte
0
∀ vGS < V P

Región triodo o resistiva

2
 I DSS
(3.9)
i D =  2 2(vGS − VTR )v DS − v DS ∀ vGS > V P ∧ 0 < v DS < vGS − V P .
 VP
Región de corriente constante o saturación

 I DSS (v − V ) 2
∀ vGS > V P ∧ v DS > vGS − V P
P
 V 2 GS
 P
[
]
Transistor de efecto de campo de metal semiconductor (MESFET) de arseniuro de galio (GaAs)
Las características del GaAs son similares a las del silicio, pero la movilidad de los
D
electrones es de 5 a 10 veces la movilidad en el silicio, razón por la cual el dispositivo
iD
puede pasar entre estados extremos (entre corte y saturación) con mayor velocidad. Se
utilizan en circuitos de radio frecuencia y circuitos digitales de alta velocidad.
iG
+
Su construcción es parecida a la de un MOSFET decremental, pero su G
vDS
+
funcionamiento muy similar al de un JFET. Su comportamiento circuital es similar
vGS
tanto al del MOSFET como al del JFET, con la diferencia que la corriente depende en
forma más marcada de vDS . La razón es que los MESFET se construyen con canales
S
cortos para aumentar su velocidad de respuestas, asi que cuando aumenta vDS y la
longitud del canal se reduce, esta reducción afecta en mayor medida a estos
dispositivos. Este fenómeno llamado modulación de la longitud del canal se cuantifica en la constante λ, llamada
parámetro de modulación de la longitud del canal.
Modulación de la longitud del canal
Las características i/v de salida tanto de los FETs como de los BJTs no son planas en la región donde la corriente se
mantiene constante respecto al voltaje del puerto de salida (llamada región de saturación para los BJTs y de
corriente constante para los FETs); sin embargo, la pendiente es mayor para los FETs, especialmente para el
MESFET. Cuando aumentamos vDS por encima del valor necesario para lograr el estrechamiento en el lado D del
canal, el voltaje vDS excedente forma parte del campo interconstituido que se forma entre el implante de drenaje y el
sustrato, sin embargo, este voltaje excedente también causa que el canal se estreche antes de llegar al drenador,
reduciendo así su longitud. La corriente que fluye por el canal es inversamente proporcional a la longitud del canal,
y por lo tanto cuando este se reduce producto del aumento de vDS , iD aumenta, produciendose una pendiente
positiva en la característica i/v de salida del dispositivo. Este efecto se cuantifica en el parámetro de modulación del
canal λ, cuyos valores típicos están entre 0.05 y 0.2 V-1 para el MESFET, entre 0.005 y 0.05 V-1 para el MOSFET y
es del orden del 10-4para el JFET.
Tomando en cuenta el parámetro de modulación de la longitud del canal, tenemos que tanto para el JFET como
para el MOSFET y el MESFET, la corriente de drenador está dada por
42
Región de corte
0
∀ vGS < VTR

Región triodo o resistiva

iD = 
2
 K 2(vGS − VTR )v DS − v DS (1 + λv DS ) ∀ vGS > VTR ∧ 0 < v DS < vGS − VTR
Región de corriente constante o saturación

 K (vGS − VTR ) 2 (1 + λv DS )
∀ vGS > VTR ∧ v DS > vGS − VTR
[
]
(3.7)
FETs canal p
El comportamiento tanto funcional como circuital de los FETs canal p es idéntico a los de canal n, pero con todos
los voltajes y corrientes con signos invertidos. La tabla 3.1 muestra la polaridad de algunos de los parámetros para
los dispositivos descritos
Tipo de dispositivo
VTR
K
vGS
vDS
iD
MOSFET-n incremental
MOSFET-p incremental
+
-
+
-
+
-
+
-
+
-
MOSFET-n decremental
-
+
+
MOSFET-p incremental
+
-
+ o -. |iD| aumenta con +
vGS más positivo
+ o -. |iD| aumenta con vGS más negativo
JFET-n
JFET-p
+
+
-
+
+
-
+
-
Modelo de FETs para bajas frecuencias
El modelo de los transistores de efecto campo se puede hallar de la misma manera que encontramos el modelo
para el BJT, o sea, identificamos la resistencia en las características i/v de los puertos de entrada y salida como las
pendientes de ellas, y asociamos fuentes de corriente de pequeña y gran señal a las características planas del
dispositivo a la salida. El resultado es un modelo como el que se presenta en la figura
G
+
rx
iD
D
iG = 0
+
+
rds
vGS = VGS + vgs
vGS
-
K(VGS – VTR)2
vDS
gmvgs
_
_
S
iS S
Fig. 3.10. Modelo de los FETs para bajas frecuencias en la región de corriente constante
43
Donde
gm =
rds ≡
∂i D
∂vGS
dv DS
di D
⇒ g m = 2 K (VGS − VTR )(1 + λV DS )
VGS , I D
=
VDS , I D
1
λK (VGS − VTR ) 2
i D = K (VGS − VTR ) 2 + g m v gs +
⇒ i D = K (VGS − VTR ) 2 +
Región de corriente constante
(3.8)
v DS
rds
V DS
v
+ g m v gs + ds
rds
rds
Dependencia de los FETs de la temperatura
La tensión umbral de estos dispositivos varía con la temperatura de la misma forma que el voltaje umbral de una
unión pn.
∆VTR ≈ # (2.5 mV/º C) ∆T para dispositivos canal n (p).
La variación de K con la temperatura se debe al aumento de las colisiones de electrones en la red cristalina,
reduciendo la movilidad. Sin embargo, la dependencia de K con la temperatura es una relación compleja, razón por
la cual se describe generalmente en forma gráfica.
44
Polarización de dispositivos de tres terminales
Conceptos fundamentales
Fuente de alimentación
Potencia de
alimentación (DC)
Amplificador (circuito con
dispositivo de tres terminales)
vi
vo
Potencia de señal (AC)
Alimentación
(DC)
señal
(AC)
Potencia de señal
amplificada (AC)
Amplificador (circuito con
dispositivo de tres terminales)
Señal amplificada
(AC + DC)
La alimentación (DC) permite preparar al amplificador para recibir la señal a ser amplificada. Esta técnica se
llama polarización, y en el caso de los transistores, permite poner a funcionar al dispositivo en la región activa
(BJT) o en la región de corriente constante (FETs). Una vez que el dispositivo funciona en la zona de interés,
podemos “superponerle” una señal de información para que sea procesada. Por ejemplo, si el amplificador está
formado por un BJT, la forma de la señal de salida se puede visualizar en la siguiente figura. A pesar que la señal de
entrada es una corriente AC ib, la señal de salida consiste en una corriente iC con componentes tanto DC como AC.
La componente AC es una reproducción amplificada de ib, y la componente DC corresponde a una corriente
suministrada por la fuente de alimentación, que permite al dispositivo trabajar en la región activa.
iC (mA)
iB = 60 µA
20
Q
10
iC (mA)
iB = 50 µA
16
iB = 40 µA
12
iB = 30 µA
8
t
vCE (V)
-10
Fig. 3.11. Variación del punto de polarización de un
amplificador con BJT al aplicar una señal
AC como corriente de entrada
10
ib (µA)
t
iB = 20 µA
45
Ilustremos la ventaja de utilizar dispositivos de tres terminales como el BJT o los FETs. Supongamos que tenemos
en el puerto de entrada (puerto 1) las corrientes i1 y v1, y en el puerto de salida (puerto 2) las corrientes i2 y v2, como
lo muestra la figura.
i1
v1
i2
Amplificador con dispositivo
de tres terminales
v2
RL
Fig. 3.12. Amplificador como fuente de corriente
Supongamos que controlamos al circuito por medio de la corriente de entrada (sería un amplificador controlado
por corriente, como los construidos con BJTs), o sea, queremos que i2 sea proporcional a i1. Si la carga varía, como
v2 = i2RL, v2 variará, pero no así i2, ya que no hemos alterado i1. Por lo tanto tenemos un circuito que mantiene la
corriente sin importar el valor de la carga, controlada solo por i1, o sea, una fuente controlada de corriente. Si i1 es
mucho menor que i2, el circuito se comporta como un amplificador; en caso que i1 es la corriente de entrada a un
BJT (ib) e i2 la corriente a la salida de este (iC), podemos observar en la característica i/v del puerto de salida del
dispositivo que realmente la corriente de salida se mantiene constante con el voltaje de salida y varia solamente con
la corriente de entrada.
De todo lo anterior podemos concluir que el problema de utilizar un amplificador se puede dividir en dos
subproblemas a) el problema de polarizarlo para que funcione en la región de interés b) el problema de introducirle
una pequeña señal que debe ser reproducida con cierta fidelidad y amplificación por el amplificador. A continuación
abordaremos el problema a), dejando b) para la próxima sección.
Para polarizar alguno de los dispositivos de tres terminales que hemos estudiado, utilizamos una red lineal de
polarización, como la que se muestra en la figura.
+
Red lineal de
polarización
_
V1
I1
Dispositivo
de tres
terminales
_
V2
+
R1
≡
I1
+
V11
Dispositivo
de tres
terminales
V1
_
_
I2
R2
+
V2
V22
I2
Fig. 3.13. Polarización de un dispositivo de tres terminales
Esta configuración nos permite plantear el siguiente sistema de ecuaciones
V1 + I1 R1 − V11 = 0
 +
V2 I 2 R2 − V22 = 0

 I 1 = g (V1 , V2 , I 2 )
 I 2 = f (V1 , V2 , I 1 )
Recta de carga de entrada
Recta de carga de salida
Característica i/v del puerto de entrada
(3.9)
Característica i/v del puerto de salida
En donde hemos asumido que el dispositivo de tres terminales está controlado por las tensiones de entada y salida
V1 y V2. Si el dispositivo fuera un BJT, estaría controlado por la corriente de entrada y la tensión de salida, mientras
que si fuera un FET estaría controlado por las tensiones de entrada y salida.
Al igual que cuando estudiamos los circuitos con dispositivos de dos terminales, podemos utilizar varios métodos
de análisis para circuitos con dispositivos de tres terminales.
46
a) Método analítico
Este método es similar al que el descrito para dispositivos de dos terminales, con la diferencia que ahora debemos
solucionar un conjunto de ecuaciones no lineales, en lugar de una sola ecuación. Por lo tanto, podemos soluciones el
problema de la siguiente forma
Se plantea el sistema de ecuaciones, consistente en las rectas de carga de entrada y salida y las características del
dispositivo de entrada y salida, como el de la ecuación 3.8
Se resuelve el sistema en forma simbólica, mediante manipulación de ecuaciones
Se manipula el sistema en forma simbólica, hasta obtener una ecuación de una incógnita, a la que se aplica un
método iterativo, como el método de Newton-Raphson en su forma escalar.
Se resuelve el sistema mediante un método iterativo, como el método de Newton-Raphson en su forma vectorial.
Ejemplo: Considere el circuito de la figura 3.13a), que incluye un dispositivo genérico de tres terminales. La
aplicación del teorema de Thevening conduce a circuito de la figura 3.13b), donde
E = 6V
i2
RA
800 kΩ
RC
5 kΩ
i2
+
+
i1
+
RC
v
72 kΩ 1
Dispositivo
genérico de
tres
terminales
v2
V11 = 0.495V
_
_
+
66.1 kΩ
R2
Dispositivo
genérico de
tres
terminales
i1
R1
≡≡
v1
_
v2
5 kΩ
_
V22 = 6V
Fig. 3.13. a) Polarización de dispositivo genérico de tres terminales b) circuito equivalente
1.Planteemos el sistema de ecuaciones
RB
72
6 = 0.495 V
V11 =
E=
72 + 800
RB + R A
R A RB
800 x72
=
= 66.1 kΩ
R A + R B 800 + 72
R1 = R A || R B =
V22 = E = 6 V
R 2 = RC = 5 kΩ
Supónga que el dispositivo genérico no lineal posee las siguientes relaciones constitutivas
 v 
i1 = 0.01v1v2 + 2 mA
i 2 = 2v1 1 - e −v2 1 + 2  mA
 50 
las rectas de carga de entrada y salida estarán dadas por
− 0.495 + 66.1 i1 + v1 = 0
− 6 + 5i2 + v 2 = 0
luego, el sistema de ecuaciones resultante será
(
)
− 0.495 + 66.1 i1 + v1 = 0
Recta de carga de entrada
− 6 + 5i2 + v 2 = 0
Recta de carga de salida
i1 =
0.01v1v2 + 2
(
mA
)
Característica de entrada
v 

i 2 = 2v1 1 - e −v2 1 + 2  mA Característica de salida
50 

47
2a. Al intentar resolver este sistema de ecuaciones, nos damos cuenta que no se puede obtener la solución simbólica
cerrada. Por lo tanto, debemos resolverlo iterativamente. Apliquemos el método de Newton-Raphson tanto en su
forma vectorial como en su forma escalar.
2b. En su forma escalar, el método de Newton-Raphson establece que
vi = vi −1 −
f (vi −1 )
df (v)
dv v =vi −1
(3.10)
lo que es simplemente una simplificación de la expresión del método para vectores.
Para poder aplicar el método de Newton-Raphson en su forma escalar, es necesario que dispongamos de una
ecuación de una sola variable; por lo tanto, debemos manipular el sistema de ecuaciones que obtuvimos en el paso 1
para obtenerla.
Manipulando el sistema de ecuaciones tenemos que
v2 − 6
v1 =
, entonces
v2 
− v2 
10 1 - e
1 + 
50 

(
)




6 − v2

f (v2 ) = −0.495 + 0.661

v2  
− v2 
1 +

10 1 - e
50  


(
v2 + 2
+
)
6 − v2
v 

10 1 - e− v2 1 + 2 
50 

(
)
pero la derivada de esta función involucra cierto grado de complejidad. La expresión resultante es




6 − v2
df (v 2 )


= 0.661

dv 2
v2  
− v2 
1 +
 
10 1 - e
 50  

v2 + 2




6 − v2


ln
 −
 10 1 - e −v2 1 + v 2  
 50  




v2 + 2

 1 − e − v2  
v 

−v


10(6 − v 2 ) e −v2 1 + 2  + 10 
  − 10 1 - e 2




50
50


6 − v2

 


− 0.661(v 2 + 2 )


v2 
 v 
−v 
10 1 - e −v2 1 + 2 (6 − v 2 )
 
10 1 - e 2 1 +
50

 
 50 

v
−

1 − e 2  
v 
 v 
−v 
10(6 − v 2 ) e −v2 1 + 2  + 10 
  − 10 1 - e 2 1 + 2 


 50 
 50 
 50  

−
2
2
v 
100 1 - e −v2 1 + 2 
 50 
(
)
(
(
)
(
)
(
(
(
)
)1 + v50 
2
−
)
)
y al aplicar el método de Newton-Raphson, obtenemos, para una inicialización de v2(0) = 3 V, v2 = 1.909384 V.
Luego v1 = 0.462522 V.
2c. En su forma vectorial, el método de Newton-Raphson establece que
(3.11)
M ( v ( k ) )∆v ( k ) = −f ( v ( k ) ) ,
∆v ( k ) = v ( k +1) − v ( k )
Manipulando las ecuaciones, tenemos que
− 0.495 + 0.661v1v2 + 2 + v1 = 0
(
)
v 

− 6 + 10v1 1 - e −v2 1 + 2  + v 2 = 0
50 

y el vector de funciones de error es
(3.12)
48
− 0.495 + 0.661v1v2 + 2 + v1



f(v) = 
v2 
=0
− v2 
1 +  + v 2 
− 6 + 10v1 1 - e
50 



el jacobiano correspondiente a este vector es


v2 + 2 v 2 + 2
0.661v1v2 + 2 ln(v1 ) 
1 + 0.661v1
v1
=0
M(v) = 

10v 1 - e −v2 1 + v 2  v1 (49 + v )e − v2 + 1 + 1


2

 1
50  5



Si inicializamos el método con v1(0) = 0.3 V y v2(0) = 3 V, obtenemos
v1 = 0.462522 V y v2 = 1.909384 V. Y sustituyendo en las características del dispositivo obtenemos
i1 = 0.490765 µA e i2 = 0.818070 mA
(
(
)
[
)
]
b) Método gráfico
El procedimiento para hallar el punto de funcionamiento del dispositivo mediante el método gráfico es el
siguiente: Sobre la característica de entrada del dispositivo se traza la recta de carga de entrada, con la que se
obtienen los puntos de intersección de esta recta de carga con la característica de entrada del dispositivo, a, b, c, ...
v2 = V2’
v2 = V2’’
i1
v2 = V2’’’
a
Ia
b
Ib
c
Ic
Va
Vb
Vb
v1
Fig. 3.15. Característica del puerto de entrada de un dispositivo genérico de tres terminales
Por ejemplo, en la figura 3.15, los puntos marcados sobre la recta de carga y sus coordenadas son
Punto
a
b
c
i1
Ia
Ib
Ic
v1
Va
Vb
Vc
v2
V2’
V2’’
V2’’’
Sobre la característica de salida del dispositivo se traza la recta de carga de salida, con la que se obtienen los puntos
de intersección de esta recta de carga con la característica de salida del dispositivo, α, β, χ, ...
49
i2
v1 = V1’
α
Iα
β
Iβ
v1 = V1’’
χ
Iχ
Vα
Vβ
v1 = V1’’’
Vχ
v2
Fig. 3.16. Característica del puerto de salida de un dispositivo genérico de tres terminales
Por ejemplo, en la figura 3.16, los puntos marcados sobre la recta de carga y sus coordenadas son
Punto
α
β
χ
I2
Iα
Iβ
Iχ
v1
V1’
V1’’
V1’’’
v2
Vα
Vβ
Vχ
Se trasladan los puntos hallados a la entrada (a1, b1, c1, ...) a la salida y se busca la intersección de la curva descrita
por los nuevos puntos y la recta de carga de salida. Este punto de intersección representa el punto de
funcionamiento en el puerto de salida (Q2).
i2
v1 = V1’
α
a
V2’
b
Q2
β
χ
V2’’
c
V2’’’
v1 = V1’’
v1 = V1’’’
v2
Fig. 3.17. Ubicación del punto de funcionamiento en el puerto de salida de un
dispositivo genérico de tres terminales
En nuestro ejemplo, el eje de las abscisas en la característica de entrada es v1 y en la característica de salida es v2.
Por lo tanto, al hacer el traslado de los puntos de entrada a la salida, ubicamos los valores de v1 y v2. Por ejemplo,
para el punto a, v1 = Va y v2 = V2’, por lo tanto, ubicamos V2’ en el eje de las abscisas, y Va como voltaje de
parametrización. Para ubicar Va es necesario interpolar entre V1’’ y V1’’’.
Se trasladan los puntos hallados a la salida (α, β, χ, ...) a la entrada y se busca la intersección de la curva descrita
por los nuevos puntos y la recta de carga de entrada. Este punto de intersección representa el punto de
funcionamiento en el puerto de entrada (Q1).
Al hacer el traslado de los puntos de salida a la entrada, ubicamos los valores de v1 y v2 para cada punto. Por
ejemplo, para el punto α, v1 = V1’ y v2 = Vα, por lo tanto, ubicamos V1’ en el eje de las abscisas, y Vα como voltaje
de parametrización. Para ubicar Vα es necesario interpolar entre V2’ y V2’’.
50
i1
v2 = V2’
Q1
v2 = V2’’
v2 = V2’’’
a1
b1
c1
V1’’’ V1’’ V1’
v1
Fig. 3.18. Ubicación del punto de funcionamiento en el puerto de entrada de un
dispositivo genérico de tres terminales
c)Método de linealización por tramos
La esencia de este método es la misma que la descrita para dispositivos de dos terminales, o sea, se reemplaza la
característica no lineal del dispositivo por aproximaciones lineales, válidas para un cierto intervalo. La construcción
de los modelos es más complicada a medida que el dispositivo tiene más terminales, ya que una variable puede
depender de más de un parámetro. En los dispositivos de tres terminales, las características de los puertos de entrada
y/o salida son familias de curvas, que deben escogerse de acuerdo a un parámetro. En el caso del BJT, la corriente
de base puede tomarse como dependiente solo de la tensión base-emisor, ya que su variación respecto a la tensión
colector-emisor es muy pequeña. Sin embargo, en el puerto de salida la corriente de colector depende de la tensión
colector-emisor y de la corriente de base, así que su característica es una familia de curvas parametrizadas en
función de la corriente de base. Un caso similar tenemos en los FETs, cuya corriente de entrada (corriente de puerta)
es siempre nula, pero su corriente de salida (corriente de drenador) depende de la tensión drenador-surtidor y está
parametrizada en función de la tensión puerta-surtidor.
Apliquemos este método en el análisis de polarización de transistores bipolares de unión (BJTs). La figura 31.9 es
un modelo obtenido sujeto a las siguientes consideraciones:
– La corriente de base es prácticamente independiente del voltaje colector-emisor; por lo tanto, el puerto de
entrada se modela siguiendo el mismo procedimiento usado para dispositivos de dos terminales.
– Es válido solo para la operación en las regiones activa y de corte
– Las pendientes (efecto Early) de todas las curvas en la característica de salida se han tomado como iguales; por
lo tanto, esta se puede modelar como una conductancia constante (Go) en el puerto de salida.
– Las curvas de la característica de salida están igualmente espaciadas para iguales variaciones de la corriente de
base, por lo que pueden modelarse como una fuente de corriente controlada por la corriente de base, con un
coeficiente βo constante.
– Se ha despreciado la corriente inversa de saturación
+
VBE
IB
IC
30 kΩ
3.75 kΩ
0.588 kΩ
00.56 V
0.6 V
0.66 V
100iB
_
+
VCE
0.07 mmohs
_
Fig. 3.19. Modelo lineal por tramos de un BJT.
Veamos el siguiente ejemplo de análisis. Busquemos el punto de funcionamiento del circuito del siguiente
circuito, utilizando el modelo de la figura 3.19.
51
VCC = 10 V
RC
5 kΩ
RB1
47 kΩ
IC
RB
IC
IB
RB2
4.7 kΩ
+
VBE -
+
VCE
-
≡≡
VBB
IB
+
VBE -
RC
+
VCE
-
VCC
R B1 R B 2
RB2
= 4.273 kΩ ;
= 0.909 V
V BB = VCC
R B1 + R B 2
R B1 + R B 2
Sustituyendo el dispositivo por su modelo lineal por tramos
RB =
IB
IC
+
RB
VBE
VBB
_
+
30 kΩ
3.75 kΩ
0.588 kΩ
00.56 V
0.6 V
0.66 V
100iB
VCE
0.07 mmohs
RC
VCC
_
Al igual que el análisis de un dispositivo de dos terminales, debemos estimar el estado de los diodos, resolver el
circuito resultante y comprobar el cumplimiento de la hipótesis. Sin embargo, en lugar de asumir los estados de los
diodos a ciegas, podemos tener una idea de ellos mediante la observación del circuito. Note que la tensión VBB es
bastante más alta que la mayor fuente que acompaña a los diodos; además, sabemos que la corriente de base es
pequeña, del orden de los microamperios, así que es probable que el transistor trabaje sobre el último tramo del
modelo lineal, o sea, todos los diodos conducen. Luego
V BB V1 V2 V3
0.909 0.54 0.6
0.66
+
+
+
+
+
+
RB
R1 R2 R3
30
3.75 0.588 = 0.667 V
= 4.27
V BE =
1
1
1
1
1
1
1
1
+
+
+
+
+
+
4.27 30 3.75 0.588
R B R1 R2 R3
como VBE > 0.66, que es la mayor de las fuentes del modelo a la entrada, la suposición de que todos los diodos
conducían era correcta, y el resultado es válido. La corriente de base será entonces
V − V BE 0.909 − 0.667
=
= 54.3 µΑ
I B = BB
4.27 k
RB
y la tensión colector-emisor está dada por
VCC
− βF IB
RC
10 mA − 100 × 54.3 × 10 −3 mA
=
= 4.271 V
VCE =
1
(1 + 0.07) mmohs
+ Go
RC
y la corriente de colector será
52
I C = β F I B + GoVCE = 5.73 mA .
El punto de funcionamiento en el puerto de entrada Q1 es igual a: IB = 54.3 µA, VBE = 0.667 V, y el punto de
funcionamiento en el puerto de salida Q2 es igual a: IC = 5.73 mA, VCE = 4.271 V. Como IC > 0 y VCE > 0.2 V,
podemos concluir que nuestra suposición de que el dispositivo operaba en la región activa (tomada en forma tácita
al utilizar el modelo) es correcta, por lo tanto, el resultado es válido.
Hemos utilizado un modelo obtenido a partir de las gráficas de las características del dispositivo, lo que puede
haber introducido un error, debido a la precisión de la representación y de las herramientas de medición; además, el
hecho de que el modelo sea una linealización de las características no lineales del dispositivo, sin duda alguna
introduce otro error, por lo que cabría preguntarse qué tan bueno es el resultado obtenido. Si aplicamos el modelo
de Ebers-Moll para el dispositivo (con αF = 0.99, αR = 0.874, ηF = ηR = 1 e IES = 15x10-15 A) y resolvemos el
circuito utilizando el método de Newton-Raphson, obtenemos como resultado IB = 52.8 µA, VBE = 0.683, IC = 5.88
mA, VCE = 4.431 V. Por lo tanto, el resultado obtenido por el modelo lineal por tramos presenta un error inferior al
4%, lo que es suficiente para la mayoria de las aplicaciones.
53
Técnicas de polarización para los BJTs
Conceptos básicos
Considere el circuito de la figura 3.20, que se utiliza como un amplificador de la señal de entrada vS (t). Como vS (t)
no tiene un componente de señal continua, el BJT no operará siempre en la región activa, sino que estará en corte
mientras que la tensión de la fuente de señal no sea capaz de polarizar en directo la unión base-emisor, o sea,
cuando vS (t) < Vγ . Sabemos que vo = VCC – iC RC , pero si iB = 0, entonces iC = 0 y vo = VCC. Por lo tanto, podemos
graficar la función de transferencia del circuito vo/vS , como se muestra en la figura 3.21.
iC
Vcc
RC
vo
iC
RB
t
Q
t
vCE
iB
+
vBE -
vS
iC
+
vCE
-
ib
Fig. 3.20. Amplificador con BJT con un punto de polarización
ubicado en la región de corte
vo
vo
Región de corte
t
Región activa
Región de saturación
Vsat
vS
t
Vγ
vS
Fig. 3.21. Función de transferencia vo/vS de un amplificador con BJT con
un punto de polarización ubicado en la región de corte
Si agregamos una fuente DC a la entrada del circuito (figura 3.22), tenemos
54
Vcc
iC
RC
iC
vo
Q
RB iB
+
vBE -
t
t
vCE
vS
iC
+
vCE
-
VΒΒ
ib
Fig. 3.22. Amplificador con BJT con un punto de polarización
ubicado en la región activa
Note que la señal AC “mueve” el punto de polarización alrededor de Q. La red de polarización debe diseñarse de tal
forma que la variación del punto de operación no saque al dispositivo de la región activa (figura 3.23).
vo
vo
t
Vsat
Vγ
t
vS
vS
Fig. 3.23. Función de transferencia vo/vS de un amplificador con BJT con
un punto de polarización ubicado en la región activa
Polarización fija
En el esquema de la figura 3.22 debiamos usar dos fuentes de voltaje DC para polarizar al dispositivo de tal forma
que las variaciones del punto de operación producidas por la fuente de entrada AC no lo sacaran de la región activa.
Sin embargo, seríamos más eficientes si lograramos este propósito con una sola fuente de tensión DC. La solución
es la polarización fija, como se muestra en la figura 3.24. Las figuras 3.24a y b muestra dos circuitos de
polarización fija, que pueden representarse mediante su equivalente de Thevening entre el emisor y la base y entre
el colector y el emisor. La figura 3.24c muestra este circuito equivalente, que es igual en estructura para ambos,
aunque varían las expresiones de los parámetros.
A partir de la figura 3.24c obtenemos las ecuaciones de los puertos de entrada y salida, que son
 R B I B + V BE − V BB = 0
,

 RC I C + VCE − VCC = 0
55
ecuaciones que junto a las características de los puertos de entrada y salida son suficientes para analizar o diseñar la
red de polarización de amplificadores con estas configuraciónes.
Vcc
Vcc
RC
R1
IC
+
VCE
-
IB
vi
+
VBE -
RC
R1
vo
IC
+
VCE
-
IB
vi
+
VBE -
R2
b)
a)
V BB = VCC
vo
R B = R1
V BB = VCC
IC
RB
≡≡
VBB
IB
+
VBE -
R2
R2 + R1
R1 R2
R2 + R1
RB =
RC
+
VCE
-
VCC
c)
Fig. 3.24. a) y b) Amplificadores con BJT usando esquemas de polarización fija. c) circuito equivalente
Ejemplo: Sea la configuración de la figura 3.24b, con VCC = 10 V, R1 = 4.7 kΩ, R1 = 47 kΩ y RC = 1 kΩ. Los
parámetros del transistor son Go = 75.8 µmohs y β F = 99 y Vγ = 0.68 V
Solución
R2
RR
= 0.909 V
V BB = VCC
R B = 1 2 = 4.27 kΩ
R2 + R1
R2 + R1
Rectas de carga
4.27 I B + V BE − 0.909 = 0

 I C + VCE − 10 = 0
Solución mediante el modelo lineal por tramos
IB
IC
+
RB
VBE
+
Vγ
β F IB
Go
VCE
VBB
_
RC
VCC
_
56
VCE =
1
(GCVCC
Go + GC
V BB − Vγ
0.909 − 0.68
= 53.6 µA
4.27k
RB
1
(1x10 −3 x10 − 99 x53.6 x10 −6 ) = 4.36 V
− βF IB )=
−5
−3
7.58 x10 + 1x10
IB =
=
I C = β F I B + GoVCE = 99 x53.6 x10 −6 + 1x10 −3 x 4.36 = 5.64 mA
Supongamos que β aumenta a 199, entonces
VCE =
1
1
(1x10 −3 x4.36 − 199 x54.6 x10 −6 ) = −0.581 V ,
(GCVCC − β F I B ) =
−5
Go + GC
7.58 x10 + 1x10 − 3
por lo tanto, el transistor no trabaja en la región activa, y el modelo que utilizamos no es aplicable, arrojando un
resultado incorrecto. El nuevo modelo será
IB
IC
+
RB
+
Vγ
VBE
VCE(sat) VCE
VBB
RC
VCC
_
IB =
IC =
_
V BB − Vγ
=
0.909 − 0.68
= 53.6 µA
4.27 x10 − 3
RB
VCC − VCE ( sat )
RC
=
10 − 0.3
= 9.7 mA
1x10 − 3
Note que β F I B = 10.67 mA > I C
Al igual que un aumento en β F lleva al BJT a saturación, un decremento lo puede llevar al corte o muy cerca de él,
distorsionando la señal amplificada. Las variaciones de VBE e ICO con la temperatura también desplazan al punto de
polarización, pudiendo este llegar a ser un problema crítico en ciertos casos. A continuación se presenta un esquema
de polarización fija realimentado que permite una mayor estabilidad del punto de polarización.
Polarización fija con estabilidad mediante resistencia de emisor
Al igual que en el esquema de polarización fija, tenemos dos configuraciones básicas (figuras 3.25a y b), y en
ambas podemos aplicar el teorema de Thevening entre los puertos de entrada y salida del BJT. A partir de la figura
3.25c obtenemos las ecuaciones de los puertos de entrada y salida,
que junto a las características del BJT
(R B + R E )I B + R E I C + V BE − V BB = 0

 R E I B + (RC + R E )I C + VCE − VCC = 0
V BE = 0.7 V

 I C = β F I B + GoVCE + (β F + 1)I CO
son suficientes para analizar o diseñar la red de polarización de amplificadores con estas configuraciones.
57
Vcc
Vcc
RC
R1
IC
+
VCE
-
IB
vi
+
VBE -
RC
R1
vo
IB
+
VBE -
vi
R2
RE
IC
+
VCE
-
vo
RE
a)
b)
V BB = VCC
V BB = VCC
R B = R1
≡≡
IB
+
VBE -
VBB
RB =
R1 R2
R2 + R1
RC
IC
RB
R2
R2 + R1
+
VCE
-
VCC
RE
c)
Fig. 3.25. a) y b) Amplificador con polarización fija con estabilidad mediante RE c)
equivalente de Thevening.
Ejemplo:
Calcular el punto de funcionamiento de un circuito con la estructura de la figura 3.25b) y VCC = 10
V, R1 = 47 kΩ, R2 = 4.7 kΩ, RC = 1 kΩ, RE = 100 Ω, VAF = 70 V, y un dispositivo de las siguientes características: a)
βF(min) = 99, VBE(max) = 0.68 V, ICO(min) = 2.15x10-15 A y b) β F(max) = 199, VBE(min) = 0.43 V, ICO(max) = 2.2x10-13 A.
Solución
Sustituyendo por el modelo lineal por tramos, tenemos el siguiente circuito
IB
IC
+
RB
VBB
VBE
+
Vγ
_
β F IB
Go
(β F+1) ICO
RC
VCE
VCC
RE
_
58
(R B + R E )I B + R E I C + Vγ − V BB = 0

 R E I B + (RC + R E )I C + VCE − VCC = 0
 I = β I + G V + (β + 1)I
F B
o CE
F
CO
 C
pero
Go =
por lo tanto I C = β F I B +
luego
entonces
IC
I
β I
≈ C ≈ F B,
V AF + VCE V AF
V AF
 V
βF IB
VCE + (β F + 1)I CO ⇒ I C = β F I B 1 + CE
V AF
 V AF


 V
(R B + R E )I B + R E  β F I B 1 + CE

 V AF



 VCE

 R E I B + (RC + R E ) β F I B 1 + V

AF



 + (β F + 1)I CO



 + (β F + 1)I CO  + Vγ − V BB = 0




 + (β F + 1)I CO  + VCE − VCC = 0




 V  
 R B + R E 1 + β F 1 + CE   I B + R E (β F + 1)I CO + Vγ − V BB = 0


 V AF  

 VCE  

  I B + (RC + R E )(β F + 1)I CO + VCE − VCC = 0
 R E + (R E + RC )β F 1 +


 V AF  
Resolviendo este sistema de ecuaciones para las condiciones dadas en a) y b), tenemos que:
IB (min) = 14.85 µA, VCE (max) = 8.19 V, IC (min) = 1.64 mA,
IB (max) = 18.5 µA, VCE (min) = 6.619 V, IC (max) = 3.981 mA.
Variaciones que representan un 24 % para IB , un 31.4 % para VCE y un 143 % para IC. Note que a pesar de la gran
variación en IC , variaciones apreciables de β F , ICO y VBE no sacan al dispositivo de la región activa.
Tarea: Solucionar para RE = 0 y observar las variaciones
Estabilidad de polarización mediante resistencia de emisor
En general, cuando se produce una variación simultánea de β F , ICO y VBE , la variación en la corriente de colector
está dada por las variaciones respecto a cada uno de estos parámetros, o sea
(3.13)
∆iC ≡ ∆iC (I CO ) + ∆iC (V BE ) + ∆iC (β F )
Si definimos los coeficientes de estabilidad respecto a cada uno de ellos como una relación que nos permite
obtener las variaciones de la corriente de colector debidas a las variaciones de los parámetros, tenemos que
i
i
i
∆iC ≡ D IC ∆I CO + D VC ∆V BE + D βC ∆β F
(3.14)
CO
siendo los coeficientes de estabilidad:
i
D IC
=
i
=
CO
D VC
BE
D iICCO ≅
R B + (β F 1
BE
F
(β F
R B + (β F
+ 1)(R B + R E )
+ 1)R E + (R B R E + R B RC + RC R E )G o
(3.15)
R B + (β F
R E Go − β F
+ 1)R E + (R B R E + R B RC + RC R E )Go
(3.16)
V − V BE + [(R B + RC )(V BB − V BE ) − R EVCC ]Go
RB + RE
x BB
+ 1)R E + (R B R E + R B RC + RC R E )Go R B + (β F 2 + 1)R E + (R B R E + R B RC + RC R E )Go
(3.17)
59
Los factores de estabilidad nos permiten visualizar en forma más clara el funcionamiento del circuito, lo que es
fundamental cuando un circuito forma parte de otro más complicado constituido por varios dispositivos. Sin
embargo, la complejidad de los factores dificulta su uso para el diseño y análisis de circuitos, y por lo tanto, es
conveniente realizar algunas simplificaciones para, a expensas de un incremento en el error, hacer más manejable
las expresiones.
La primera simplificación que haremos será despreciar el efecto Early, o sea, tomar Go = 0. Las expresiones
resultantes son:
(β + 1)(R B + R E )
i
(3.18)
D IC = F
CO
R B + (β F + 1)R E
i
D VC
BE
D iβCF ≅
=
− βF
R B + (β F + 1)R E
(3.19)
RB + RE
V BB − V BE
RB + RE
x
I C1 .
≅
R B + (β F 1 + 1)R E R B + (β F 2 + 1)R E β F 1 [R B + (β F 2 + 1)R E ]
Podemos hacer una simplificación adicional. Si consideramos el caso en que β F 1
i
D IC
CO
i
D VC
BE
y si β F 2
RE
>> 1 , entonces
RB
D iβCF ≅
RE
>> 1 , entonces
RB
≅1
=
(3.20)
(3.21)
−1
RE
(3.22)
RB + RE
I C1
β F1 β F 2 RE
(3.23)
RE
>> 1 no son siempre
RB
aplicables, es más, se podría decir que en la mayoría de las aplicaciones RB >> RE , y por lo tanto, la condición no se
cumple sino en casos donde β F1,2 sea muy grande.
Esta última simplificación debe tratarse cuidadosamente, ya que las condicines β F 1, 2
Ejemplo
Para un transistor con VAF = 70 V y la configuración mostrada en la fig. 3.26, deseamos diseñar una red de
polarización que reduzca las variaciones de IC de forma que para β F = 99, VBE = 0.68 V e ICO = 2.15x10-15 A se tenga
un punto de polarización de IC = 1 mA y VCE = 6 V, y para β F = 199, VBE = 0.43 V e ICO = 2.2x10-13 A se tenga un
punto de polarización de IC = 1.3 mA.
Solución
Vcc
RC
R1
IB
vi
R2
+
VBE -
IC
+
VCE
-
IC
vo
RB
≡≡
VBB
IB
+
VBE -
RC
+
VCE
RE
RE
Fig. 3.26. Ejemplo de polarización fija con estabilización por RE
VCC
60
Queremos que el circuito a diseñar permita al dispositivo funcionar en las siguientes condiciones (estados):
Estado 1
βF1 = 99
VBE1 = 0.68 V
ICO1 = 2.15x10-15 A
IC1 = 1 mA
VCE = 6 V
Estado 2
βF2 = 199
VBE2 = 0.43 V
ICO2 = 2.2x10-13 A
IC2 = 1.3 mA
Variaciones
∆β F = 100
∆VBE = -0.25 V
∆ICO = 2.18x10-13 A
∆IC = 0.3 mA
I C1
= 13.2 µmohs
V AF + VCE1
y podemos obtener la corriente de base en el estado 1 a partir de la siguiente expresión
I − I CO1 ( β F 1 + 1) − GoVCE1
= 9.21 µA
I B1 = C1
β F1
Planteemos el sistema de ecuaciones que nos permita solucionar el problema. Sea

 I (R + R ) + I R + V
E
B1 E
CE1 − VCC = 0
 C1 C
 I C1 R E + I B1 (R E + R B ) + V BE1 − V BB = 0

(R E + R B )I C1
(β + 1)(R E + R B )
− β F1
∆I C = ∆V BE
+ ∆I CO F1
+ ∆β F
β F1 (R B + (β F 2 + 1)R E )
R B + R E (β F 1 + 1)
R B + (β F 1 + 1)R E

Sabemos que
Go =
Note que las incógnitas en nuestro sistema de ecuaciones son RC , RE , RB y VBB , o sea, cuatro incógnitas en un
sistema de tres ecuaciones. Como nuestro problema es de diseño, superamos esta dificultad estableciendo
arbitrariamente una de las variables. Esto no imposibilita alcanzar los requerimientos del diseño, pues no tenemos
más ecuaciones que impongan restricciones; en caso de contar con una cuarta ecuación, tendríamos que resolver el
sistema de ecuaciones sin asumir ningún valor arbitrariamente; de hacerlo así, no podríamos cumplir con los
requerimientos de diseño.
La primera de las ecuaciones en nuestro sistema relaciona RC y RE. Es una elección razonable asumir el valor de
RC , ya que esta resistencia representa la carga para muchos amplificadores, y determina en muchas configuraciones
la resistencia de salida, tema que trataremos en la próxima sección. Sea RC = 1 kΩ, entonces
V − VCE1 − I C1 RC
= 2.97 kΩ
R E = CC
I C1 + I B1
Y nuestro sistema de ecuaciones se reduce a dos ecuaciones con dos incógnitas, o sea, RB y VBB . Luego
 I C1 R E + I B1 (R E + R B ) + V BE1 − V BB = 0

(R E + R B )I C1
(β F1 + 1)(R E + R B )
− β F1

∆I C = ∆V BE R + R (β + 1) + ∆I CO R + (β + 1)R + ∆β F β (R + (β + 1)R )
B
E
F1
B
F1
E
F1 B
F2
E

Resolviendo obtenemos RB = 1.9084 kΩ y VBB = 5.45549 V. Sabemos que
R1 R2

RB = R + R

1
2
⇒ R1 = 349.81 kΩ y R1 = 419.936 kΩ

V = VCC R2
 BB R1 + R2
Solución VCC = 10 V, RC = 1 kΩ, R E = 3 kΩ, R1 = 360 kΩ, R 2 = 430 kΩ
Con los valores exactos obtenemos una desviación despreciable en IC1 y VCE1, mientras que para IC2 obtenemos un
valor de 1.289 mA, lo que representa un error de 0.826 %. Con los resistores aproximados a valores comerciales, los
resultados para IC1 , IC2 y VCE1 son 0.99188 mA, 6.0048 V y 1.277 mA respectivamente, lo que representa
desviaciones de 0.811, 1.757 y 0.08 %, respectivamente, resultados satisfactorios para la mayoría de las
aplicaciones.
61
Podemos solucionar el problema sin usar los factores de estabilidad. En este caso, lo que hacemos es plantear un
sistema de ecuaciones que incluya las rectas de cargas y las características del dispositivo en ambos estados. Al
igual que anteriormente, calculamos Go e IB1 de la siguiente forma:
I C1
= 13.2 µmohs
Go =
V AF + VCE1
I − I CO1 ( β F 1 + 1) − GoVCE1
= 9.21 µA
I B1 = C1
β F1
V − VCE1 − I C1 RC
Si igualmente asumimos RC = 1 kΩ,
= 2.97 kΩ ,
R E = CC
I C1 + I B1
el sistema de ecuaciones resultante es
 I C1 R E + I B1 (R E + R B ) + V BE1 − V BB = 0

 I C 2 R E + I B 2 (R E + R B ) + V BE 2 − V BB = 0
,

 I C 2 (RC + R E ) + I B 2 R E + VCE 2 − VCC = 0
 I C 2 = I B 2 β F 2 + I CO 2 (β F 2 + 1) + GoVCE 2

el cual es un sistema de cuatro ecuaciones, a partir del cual obtenemos RB , VBB , IB2 y VCE2 . Finalmente, RB = 204.74
kΩ y VBB = 5.585 V, valores con los que obtenemos R1 = 366.6 kΩ y R2 = 463.71 kΩ. Estos valores producen
resultados exactos, con una desviación nula respecto al punto de polarización deseado. Podemos concluir que la
consideración de ambos estados sin utilizar los factores de estabilización arroja resultados exactos, a diferencia de
los resultados aproximados obtenidos con los factores. Sin embargo, sin los factores debemos solucionar un sistema
de cuatro ecuaciones, reduciendose a dos ecuaciones si usamos los factores, aunque sean ellas de mayor
complejidad.
Estabilización mediante resistencia de realimentación entre colector y base
Vcc
En la configuración mostrada por las figuras 3.24 y 3.25,
lograbamos la estabilidad del punto de polarización debido
a que cualquier aumento en la corriente de colector
produce una disminución de la tensión colector-emisor (el
punto de funcionamiento se desplaza hacia arriba por la
recta de carga). En la fig. 3.27 vemos que
V − V BE
I B = CE
,
RF
por lo tanto en esta estructura, una disminución en VCE
producirá una disminución en la corriente de base, que se
opondrá al aumento de IC.
El sistema de ecuaciones resultante es
 I C = β F I B + (β F + 1)I CO + GoVCE

 I B R F + V BE − VCE = 0
(I + I )(R + R ) + V − V = 0
B
C
E
CE
CC
 C
RC
vo
RF
vi
IB
+
VBE -
IC
+
VCE
RE
Fig. 3.27. Configuración de estabilización mediante
resistencia de realimentación entre colector y
base
Estabilización mediante diodos
Para el circuito de la figura 3.28a), calculemos sus equivalentes de Thevening en los puertos de entrada y salida
del BJT, como se muestra en la figura 3.28b). Si despreciamos la resistencia en el diodo, tenemos que
R (V − V D )
R V − R1V D
R2 R1
y RB =
+ V D = 2 CC
V BB = 2 CC
R1 + R2
R1 + R 2
R1 + R2
62
Sabemos que la tensión base-emisor disminuye con la temperatura. En un circuito como el de la figura 3.28b), la
corriente de base aumenta cuando disminuye la tensión base emisor, ya que
V − V BE − V E
I B = BB
RB
pero
V E = R E (I C + I B ) ≅ I B R E (β F + 1)
V BB − V BE
luego
IB =
R B + R E (β F + 1)
si no existiese el diodo en la figura 3.28a), la tensión VBB sería constante; en ese caso, es claro que la corriente de
base aumentaría con una disminución de la tensión base-emisor VBE .
R V − R1V D
Si el diodo existiese, sabemos que V BB = 2 CC
, en ese caso
R1 + R2
Vcc
RC
R1
IB
vi
+
VD
_
R2
ID
+
VBE -
IC
+
VCE
_
IC
≡≡
RB
vi
VBB
IB
+
VBE -
RC
+
VCE
-
VCC
RE
RE
b)
a)
Fig. 3.28. a) Configuración de estabilización mediante diodos. b) Equivalente de Thevening
 R2VCC − R1V D

 R2VCC
R (V − V BE ) R2V BE 
1
− V BE  =
+ 1 D
−



R B + R E (β F + 1) 
R1 + R2
R1 + R2
R1 + R2 
 R B + R E (β F + 1)  R1 + R2
si la unión base-emisor del BJT y el diodo están pareados, o sea, VD = VBE , entonces
 R2VCC
RV 
1
− 2 BE  .
IB =

R B + R E (β F + 1)  R1 + R2 R1 + R2 
Note que la corriente de base aún depende de la tensión base-emisor, y que una disminución en ella provoca un
aumento en IB . Sin embargo, la dependencia ahora es menor, especificamente se ha reducido la dependencia de la
R2
.
corriente de base respecto a la tensión base-emisor en un factor igual a
R1 + R 2
IB =
1
63
Técnicas de polarización de FETs
Polaricemos el dispositivo de la figura 3.29 en la mitad de su región de corriente constante. Un dispositivo
polarizado de esta forma, permite el procesamiento de una señal simétrica (respecto al eje de voltaje) de máxima
amplitud sin que sufra distorsión, o sea, sin llevar al dispositivo a la región triodo o de corte; esta forma de
polarización se llama polarización para máxima excursión simétrica.
iD RD = 5 kΩ
RG
vi
iG
+
vGS
_
+
vDS
-
VDD = 10 V
K = 0.5 mA/V2
VTR = 2 V
VGG
Fig. 3.29. Amplificador con MOSFET
La recta de carga del puerto de salida es
V DS + I D R D − V DD = 0
Si queremos que VDS esté en el centro de la región de corriente constante, entonces
V − 1.8
= 5.9 V
V DS = 1.8 + DD
2
ya que VDD y 1.8 V son los límites de entrada a las regiones de corte y triodo respectivamente.
La corriente de drenador la podemos hallar graficamente o por medio de
V − V DS
= 0.82 mA .
I D = DD
RD
Si suponemos que λ = 0, en la región de corriente constante
ID
+ VTR = 3.28 V ,
I D = K (VGS − VTR )2 ⇒ VGS =
K
luego, VGS = 3.28 V y excursionara entre 2 V y 3.8 V, o sea entre los límites de corte y saturación. Por lo tanto, para
lograr una amplificación sin distorsión, la señal AC no debe ser mayor de 3.8 – 2 = 1.8 Vpp. En caso que la señal de
entrada excursione fuera de estos límites, la señal de salida quedaría distorsionada. Note que la excursión de la señal
de entrada no es simétrica, aún cuando en la salida si lo es. Esto se debe a que la dependencia de la corriente de
drenador iD , (y por lo tanto de vDS si la carga es una resistencia), respecto a VGS es una función cuadrática. Por lo
tanto, la amplitud de las señales de entrada (vGS) y salida (vDS) deben ser
3.8 V (máximo)
+ 0.52 V
pero VGS = 3.28 V ⇒ v gs = 
vGS = VGS + v gs = 
2 V (mínimo)
− 1.28 V
10 V (máximo)
+ 4.1 V
pero V DS = 5.9 V ⇒ v ds = 
v DS = V DS + v ds = 
1.8 V (mínimo)
− 4.1 V
Nota: el límite donde comienza la región triodo se puede calcular analíticamente resolviendo el sistema de
ecuaciones compuesto por
 I D = K (VGS − VTR ) 2

V DS = VGS − VTR
V + I R − V = 0
D D
DD
 DS
64
Polarización fija
VDD
RC
RA
iG
vi
+
vGS
RB
_
iD
+
vDS
_
RD
iD
vo
RG
iG
+
vGS
_
+
vDS
-
VGG
a)
b)
Fig. 3.30. Amplificador con MOSFET usando un esquema de polarización fija.
Ejemplo: Determine el punto de polarización del MOSFET de la figura 3.30 si VDD = 16 V, RD = 2 kΩ, RA = 1.5
MΩ, RB = 500 kΩ, K = 1 mA/V2 , VTR = 2 V y λ = 0.
RB
= 4 V I D = K (VGS − VTR )2 = 4 mA V DS + R D I D − V DD ⇒ V DS = 16 − 4 x 2 = 8 V
VGG = V DD
R A + RB
Tarea: resolver para λ = 0.01 V-1.
Autopolarización y polarización fija combinadas (estabilización mediante resistencia de surtidor)
VDD
RC
RA
iG
vi
RB
+
vGS
_
iD
+
vDS
_
RD
iD
vo
RG
≡
iG
+
vGS
VGG
_
+
vDS
-
VDD
RS
RS
a)
b)
Fig. 3.31. a) Esquema de autopolarización y polarización fija combinadas b) cirucuito equivalente
VGG = V DD
RB
R A + RB
VGS + I D R S − VGG = 0

V DS + I D (R D + R S ) − V DD = 0

2
 I D = K (VGS − VTR )
Si λ ≠ 0
I D = K (VGS − VTR ) 2 (1 + λV DS )
65
En la segunda parte de estos apuntes, trabajamos con un dispositivo genérico llamado de ley cuadrática, con
características i/v muy similares a la de los FETs operando en la región de saturación. En esa ocasión usamos el
método gráfico para buscar su punto de operación; de la misma manera, podemos relacionar el vGS con iD para
obtener una característica de transferencia que nos permita tratar a un FET de una forma similar al dispositivo de ley
cuadrática. Del circuito de la figura 3.31b) podemos concluir que
1

 I D = − R (VGS − VGG ) Recta de carga de transferencia
S

 I = K (V − V ) 2
característica de transferencia
GS
TR
 D
Las líneas punteadas de la figura 3.32a) muestran las desviaciones cuando consideramos la dependencia de ID
respecto a VDS por efecto de la modulación de la longitud del canal.
i1
I D = K (VGS − VTR ) 2 (1 + λV DS )
I D = K (VGS − VTR ) 2
RG
ID
a)
1
(VGS − VGG )
=−
RS
RD
iD
iG
+
vGS
+
vDS
-
_
VGG
VDD
RS
b)
v1
Fig. 3.32. Dependencia de ID respecto al efecto de modulación de la longitud del canal
D
Polarización de FETs como fuente de corriente
Las características del JFET y el MOSFET decremental mediante la
cual pueden funcionar en la región de saturación aún cuando su voltaje
puerta-surtidor sea nulo, nos permite utilizarlos como fuentes de
corriente usando las configuraciones de la figura 3.33. Si vDS es tal que
los dispositivo operen en la región de saturación, como vGS es constante
(nulo), al variar la carga por la que fluye la corriente I0, varia la recta de
carga pero esta se mueve sobre las característica casi plana del
dispositivo, así que la corriente I0 se mantiene aproximadamente
constante. Es posible lograr esto mismo con MOSFETs incrementales,
D
I0
+
vDS
_
I0
+
vDS
_
I0
I0
S
S
Fig. 3.33. MOSFET como fuente
de corriente
pero se debe polarizar la tensión puerta-surtidor con una fuente de
tensión, lo que es una desventaja considerable.
VDD
Estabilización mediante resistencia entre drenador y fuente
Sabemos que la corriente que circula por la puerta es cero, así que
de igual forma, IF = 0, y por lo tanto, VGS = VDS . Si aumenta ID , nos
desplazamos hacia arriba por la recta de carga, disminuyendo VDS.
Pero al disminuir VDS, disminuye también VGS, y esta disminución se
opone al aumento de la corriente de drenador.
VGS + I D R D − V DD = 0

 I D = K (VGS − VTR ) 2
note que al conectar los terminales de drenador y puerta, VGS = VDS,
y si sustituimos en la ecuación del dispositivo, tenemos que
RC
iF
vo
RF
vi
+
vGS
_
iD
+
vDS
_
Fig. 3.34. Estabilización de FETs mediante
resistencia entre drenador y fuente.
66
I D = K (V DS − VTR ) 2 .
Anteriormente hemos mencionado que una desventaja de los FETs es el
suministrar una salida asimétrica para una entrada simétrica, ya que la relación
entre la variable de control (vGS ), y la variable controlada (iD) es una relación
cuadrática, pero, ¿que sucede si conectamos una carga no lineal, que compense la
no linealidad del dispositivo?. Esta carga es tal que la tensión entre sus
terminales está dada por
V DS =
ID
+ VTR
K
+
vGS
iD
+
vDS
_
_
Fig. 3.35. Carga NMOS
y es útil al diseñar circuitos con tecnología NMOS.
Polarización de un amplificador NMOS
VDD
v o = v DS1 = V DD − v DS 2 , i D1 = i D 2 ,
si ambos dispositivos trabajan en la región de corriente constante
I D1 = K 1 (VGG − VTR1 )2 , I D 2 = K 2 (VGS 2 − VTR 2 )2
luego
I
1
VGS 2 = D 2 + VTR 2 =
K1 (VGG − VTR1 )2 + VTR 2
K2
K2
⇒ VGS 2 =
+
vGS2
vo
K1
(VGG − VTR1 ) + VTR 2 = V DS 2
K2
y finalmente
⇒ Vo = V DD −
K1
(VGG − VTR1 ) − VTR 2
K2
_
iD2
+
vDS2
_
vi
+
vGS1
_
iD1
+
vDS1
_
VGG
Fig. 3.36. Amplificador NMOS
67
ANÁLISIS DE PEQUEÑA SEÑAL EN CIRCUITOS CON DISPOSITIVOS DE TRES TERMINALES
Las funciones principales que por lo común cumple un circuito electrónico a frecuencias medias son las
siguientes:
ƒ Escalamiento: Consiste en cambiar los niveles de una señal aplicada a su entrada para producir a la salida una
réplica escalada de la misma, libre de distorsión. El cambio de los nivel de tal forma que la amplitud de la señal de
salida sea mayor que la de la entrada se llama amplificación, en caso contrario se obtiene una atenuación.
ƒ
Generación: Consiste en producir señales de diferentes tipos (como sinusoidales, triangulares, trenes de pulsos,
etc.).
ƒ
Conformación: Consiste en el cambio de la forma de una señal. Como ejemplo podemos citar los circutos
recortadores y fijadores con diodos estudiados anteriormente.
ƒ
Conmutación: Consiste en activar o desactivar cierta parte de un circuito, de tal forma que su funcionamiento
esté condicionado por una señal de control. Como ejemplo podemos citar los circuitos con diodos que cambian su
estructura dependiendo del estado de conducción de los diodos.
En este curso limitaremos nuestro estudio a los circuitos conformadores y de escalamiento. Los circuitos
conformadores han sido tratados anteriormente mediante dispositivos de dos terminales, mientras que los circuitos
de escalamiento, que en adelante llamaremos amplificadores aunque produzcan atenuación, los estudiaremos como
constituidos por dispositivos de dos terminales, en un rango de frecuencias que denominaremos frecuencias medias.
Tipos de amplificadores
La misión de un amplificador es tomar la señal aplicada a su entrada sin consumir potencia de la fuente de señal y
producir una versión escalada de la misma en su salida cuyo valor no dependa de la carga. Dependiendo de la
naturaleza de las señales de entada y salida, o sea, si son fuentes de corriente o voltaje, podemos clasificar a los
amplificadores de la siguiente forma:
Amplificadores de voltaje
La señal de entrada es una fuente de voltaje, y a la salida se obtiene una versión escalada de la misma. Idealmente,
El amplificador de voltaje debe tomar la señal de voltaje aplicada a su entrada sin consumir corriente de la fuente de
señal, o sea, reproducirlo integramente a la entrada del amplificador, y producir una versión escalada independiente
de la carga. Esta labor puede realizarla una fuente ideal de voltaje controlada por voltaje, pero este es un modelo
cuyo comportamiento se aleja del comportamiento real de los amplificadores de voltaje. Para caracterizar el
comportamiento no ideal de estos amplificadores, incluimos una resistencia Ri en serie con la fuente de señal en el
puerto de entrada del amplificador y una resistencia Ro también en serie en el puerto de salida, como se muestra en
la figura 4.1. Esta claro que para un amplificador ideal, Ri debe ser infinita (para que toda la tensión de entrada esté
entre sus terminales) y Ro debe ser igual a cero (para que la caida de tensión entre sus terminales sea nula). Sin
embargo, en la práctica estos límites son inalcanzables, y por lo tanto al diseñar un amplificador de voltaje es
suficiente lograr que Ri se mucho mayor que la resistencia de la fuente de señal RSV, mientras que Ro sea mucho
menor que la resistencia de carga RL .
Amplificador de voltaje
ii
RSV
Ro
vi
_
AV =
+
+
vs
vo
: Ganancia de voltaje en
vi
circuito abierto (RL = ∞)
io
RI
+
A V vi
_
vo
_
RL
Ri:
Resistencia de entrada
Ro:
Resistencia de salida
Fig. 4.1. Amplificador de voltaje
68
Amplificadores de corriente
La señal de entrada es una fuente de corriente, y a la salida se obtiene una versión escalada de la misma.
Idealmente, El amplificador de corriente debe tomar la señal de corriente aplicada a su entrada sin consumir
corriente de la fuente de señal, o sea, lograr que la corriente generada por la fuente circule integra por la entrada del
amplificador, y producir una versión escalada independiente de la carga. Esta labor puede realizarla una fuente ideal
de corriente controlada por corriente, pero este es un modelo cuyo comportamiento se aleja del comportamiento real
de los amplificadores de corriente. Para caracterizar el comportamiento no ideal de estos amplificadores, incluimos
una resistencia Ri en paralelo con la fuente de señal en el puerto de entrada del amplificador y una resistencia Ro
también en paralelo en el puerto de salida, como se muestra en la figura 4.2. Esta claro que para un amplificador
ideal, Ri debe ser igual a cero (para que toda la corriente circule por ella) y Ro debe ser infinita (para que toda la
corriente circule por la carga). Sin embargo, en la práctica estos límites son inalcanzables, y por lo tanto al diseñar
un amplificador de corriente es suficiente lograr que Ri se mucho menor que la resistencia de la fuente de señal RSV,
mientras que Ro sea mucho mayor que la resistencia de carga RL .
Amplificador de corriente
ii
io
RSV vi
IS
AI =
+
+
vo
RO
RI
AI ii
_
RL
_
io
: Ganancia de corriente en
ii
corto circuito (RL = 0)
Ri:
Resistencia de entrada
Ro:
Resistencia de salida
Fig. 4.2. Amplificador de corriente
Amplificadores de transresistencia
La señal de entrada es una fuente de corriente, y a la salida se una señal de voltaje proporcional a la corriente de
entrada. Idealmente, El amplificador de transresistencia debe tomar la señal de corriente aplicada a su entrada sin
consumir corriente de la fuente de señal, o sea, lograr que la corriente generada por la fuente circule integra por la
entrada del amplificador, y producir una tensión a la salida proporcional a la corriente de entrada independiente de
la carga. Esta labor puede realizarla una fuente ideal de voltaje controlada por corriente, pero este es un modelo
cuyo comportamiento se aleja del comportamiento real de los amplificadores de transresistencia. Para caracterizar el
comportamiento no ideal de estos amplificadores, incluimos una resistencia Ri en paralelo con la fuente de señal en
el puerto de entrada del amplificador y una resistencia Ro también en serie en el puerto de salida, como se muestra
en la figura 4.3. Esta claro que para un amplificador ideal, tanto Ri como Ro deben ser iguales a cero (para que toda
la corriente circule por Ri y no haya caida de voltaje en Ro). Sin embargo, en la práctica estos límites son
inalcanzables, y por lo tanto al diseñar un amplificador de transresistencia es suficiente lograr que Ri sea mucho
menor que la resistencia de la fuente de señal RSV y Ro sea mucho menor que la resistencia de carga RL .
Amplificador de transresistencia
ii
Ro
IS
RSV
_
Rm =
+
+
vi
io
RI
+
Rm ii
_
vo
_
vo
: Transresistencia en circuito
ii
abierto (RL = ∞)
RL
Ri:
Resistencia de entrada
Ro:
Resistencia de salida
Fig. 4.3. Amplificador de transresistencia
69
Amplificadores de transconductancia
La señal de entrada es una fuente de voltaje, y a la salida se obtiene una corriente proporcional a la magnitud del
voltaje de entrada. Idealmente, el amplificador de transconductancia debe tomar la señal de voltaje aplicada a su
entrada sin consumir corriente de la fuente de señal, o sea, reproducirlo integramente a la entrada del amplificador,
y producir una corriente proporcional al voltaje de entrada independiente de la carga. Esta labor puede realizarla una
fuente ideal de corriente controlada por voltaje, pero este es un modelo cuyo comportamiento se aleja del
comportamiento real de los amplificadores de transconductancia. Para caracterizar el comportamiento no ideal de
estos amplificadores, incluimos una resistencia Ri en serie con la fuente de señal en el puerto de entrada del
amplificador y una resistencia Ro en paralelo en el puerto de salida, como se muestra en la figura 4.4. Esta claro que
para un amplificador ideal, tanto Ri como Ro deben ser infinitas de tal forma que toda la tensión de entrada esté entre
los terminales de Ri y la corriente de salida circule toda por la carga RL. Sin embargo, en la práctica estos límites son
inalcanzables, y por lo tanto al diseñar un amplificador de voltaje es suficiente lograr que Ri se mucho mayor que la
resistencia de la fuente de señal RSV, y que Ro sea mucho mayor que la resistencia de carga RL .
Amplificador de transconductancia
ii
RSV
io
+
+
vi
vs
Gm =
vo
RO
RI
Gm vi
_
io
: Transconductancia en
vi
corto circuito (RL = 0)
RL
_
Ri:
Resistencia de entrada
Ro:
Resistencia de salida
Fig. 4.4. Amplificador de transconductancia
Análisis de pequeña señal en circuitos con dispositivos de tres terminales
VO
Vcc
RB
RL
R1
iB
vs
IB
R2
+
vBE -
iC
+
vCE
-
vO
+
VBE -
VBB
≡≡
+
VCE
-
a)
VCC
iC
iB
RS
vs
RL
IC
+
vBE -
+
vCE
-
RB
vo
RL
b)
Fig. 4.5. Análisis un amplificador con BJT a) de polarización, b) pequeña señal
La tensión de salida vO está dada por vO = VO + v o . Podemos dividir el análisis en dos secciones, una análisis de
polarización para determinar VO, y un análisis de pequeña señal para hallar vo.
– Análisis de polarización:
VO = VCC + I L R L = VCC − I C R L
70
si sustituimos al transistor por su modelo de polarización, obtenemos el siguiente circuito
VO
IC
rbe
RB IB
+
+
VBE
VBB
IL
RL
GO
Vγ
β F IB
VCC
VCE
(β F+1) ICO
_
Fig. 4.6. Análisis de polarización
De la figura 4.6 podemos observar que
I C = β F I B + (β F + 1)I CO + GoVO
luego,
VO =
1
[VCC − RL β F I B − RL (β F + 1)I CO ]
1 + R L Go
pero
IB =
V BB − Vγ
R B + rbe
⇒ VO =
1
1 + R L Go
V BB − Vγ


− R L (β F + 1)I CO 
VCC − R L β F
R B + rbe


con rbe = rb’e + rx.
En la mayoria de las aplicaciones R L G o << 1 , rbe << R B y β F I B >> I CO (β F + 1) , entonces
VO = VCC − R L β F
V BB − Vγ
RB
Esta última expresión de VO la pudimos haber obtenido directamente desde el circuito de la figura 4.5, sin
necesidad de sustituir al BJT por su modelo de polarización. Note que si tomamos I C = β F I B e I B =
tenemos directamente que
VO = VCC − RL I C = VCC − RL β F I B = VCC − R L β F
VBB − Vγ
RB
– Análisis de pequeña señal:
Sustituyendo por el transistor por su modelo de pequeña señal en la figura 4.7.
ic
rx
ib
RS
+
+
vs
RB
vbe
RB’E
GO
β o ib
Fig. 4.7. Análisis de pequeña señal
vce
_
vo
RL
.
V BB − Vγ
RB
,
71
v o = −i c R L
i c = β o ib + v o Go = β o ib − i c R L G o ⇒ i c =
pero
vo = −
entonces
β o ib
1 + R L Go
RL β o ib
1 + R L Go
Análisis lineal de circuitos de con BJTs
Procedimiento
1.
2.
3.
4.
5.
Hallar el punto de polarización (Q).
Señalar sobre el diagrama de conexiones los terminales de base (puerta), colector (drenador) y emisor (surtidor)
Hallar los parámetros del modelo de pequeña señal rbe y Go (gm y rds)
Sustituir el transitor por su modelo de pequeña señal.
Hallar las características del amplificador. Algunas características de interés son:
a) La ganancia de corriente AI =
io
ii
vo
vi
v
La resistencia de entrada Ri = i
ii
v
La resistencia de salida Ro = o
io
v
La transresistencia R m = o
ii
i
La transconductancia G m = o
vi
b) La ganancia de tensión AV =
c)
d)
e)
f)
Configuración de emisor común
ic
RS
ib
+
vbe -
vs
+
vce
-
Ri
+
+
RL
RB
Ri’
ic
rx
ib
RS
vo
≡≡ vs
RB
vbe
RB’E
GO
β o ib
vce
_
Ro’
Ro
Fig. 4.8. Configuración de emisor común
a) Resistencia de entrada Ri =
Ri =
vi
ii
v i v b ib rbe
=
=
= rbe
ii
ib
ib
Ri ' =
vs
r R
= Ri || R B + R S = R S + be B
is
rbe + R B
vo
RL
72
si
Ri ' = Ri ≈ rbe
RB >> rbe y RS<<rbe , entonces
b) Ganancia de corriente AI =
io
ii
−
β o ib
βo
1 + R L Go
=−
1 + RL Go
ib
i o il − i c
= =
=
ii ib
ib
i
i
si queremos hallar AIS = o = l debemos hacer un divisor de corriente entre Ri y RB ,
is is
AI =
ib = i s
RB
,
R B + rbe
entonces
βo
io
RB
=−
is
R B + rbe 1 + R L G o
si RL Go << 1 y RB >> rbe , entonces AIS ≈ AI ≈ − β o
AIS =
c) Ganancia de corriente AV =
vo
vb
ib β o R L
β o RL
1 + Go RL
v
AV = o =
⇒ AV = −
vb
i b rbe
rbe (1 + Go R L )
v
y la ganancia de tensión vista desde vs AVS = o
vs
v s = i s R S + ib rbe
pero
RB i s
ib =
y además
R B + rbe
R +r
v s = B be RS ib + rbe ib
entonces
RB
i β R
− b o L
1 + Go R L
v
− β o RL
=
AVS = o =
por lo tanto
vs




R + rbe
R + rbe
ib  rbe + B
RS  (1 + Go R L ) rbe + B
RS 
RB
RB




β
R
− o L
si RL Go << 1 y RB >> rbe , entonces AVS ≈
rbe + RS
−
Podemos hallar la ganancia de tensión en función de la ganancia de corriente y la resistencia de entrada, tomando
en cuenta que
AV =
vo RL io
R
=
= AI L .
vi
Ri i i
Ri
73
Sin embargo, es necesario utilizar esta relación cuidadosamente, ya que la ganancia de tensión está relacionada a
vo
,
vb
una determinada ganancia de corriente, carga y resistencia de entrada. Por ejemplo, si queremos hallar AV =
usamos como ganancia de corriente AI =
io
, RL como carga y Ri como resistencia de entrada, de tal forma que
ib
AV =
vo R L io R L
AI
=
=
v b Ri i b
Ri
i
vo
usamos como ganancia de corriente AIS = o , RL como carga y Ri’ como
vS
is
pero si queremos hallar AVS =
resistencia de entrada, de tal forma que
AVS =
v o R L io R L
AIS
=
=
v s Ri ' i s Ri '
¿que pasaría si usaramos Ri como resistencia de entrada para hallar AV?. Tendríamos que
R i
v
RL
AIS = L o ≠ o = AVS
Ri
Ri i s v s
y obtendríamos un valor incorrecto para la ganancia de tensión AVS .
d) Resistencia de salida Ro =
v2
i2
Las variables v2 e i2 no está señaladas en la figura 4.9 porque debemos modificar este circuito para hallarla. La
resistencia de salida se define como la obtenida al anular la fuente de entrada (ponerla a cero si es una fuente de
tensión o abrirla si es una fuente de corriente) y hacer en infinita la resistencia de carga.
i2
RS
iB
+
vBE -
+
vCE
-
v2
ib
RS
i2
≡≡
RB
RB’E
GO
i2
β o ib
RB
Ro
Ro
Fig. 4.9. Resistencia de salida
Ro =
i 2 v2
rx
v
v2
1
(1 − β o ib ) ,
, si i2 = 1 A, entonces Ro = 2 =
i2
1 Go
pero en el puerto de entrada observamos que ib = 0, entonces
Ro =
1
Go
Si quisieramos hallar la resistencia de salida Ro’ que incluya la resistencia de carga RL ,
Ro ' =
RL
1 + Go R L
74
si G o → 0 , entonces R o → ∞, R o ' = R L
ib β o R L
β o RL
1 + Go RL
v
e) Transresistencia R m = o =
.
⇒ Rm = −
1 + Go R L
ib
ib
βo
v
i R
RL
Podemos llegar al mismo resultado considerando que R m = o = o L = AI R L = −
1 + Go R L
ib
ib
β o ib
−
βo
1 + RL Go
i
g) Transconductancia G m = o =
=−
vb
ib rbe
rbe (1 + R L G o )
i
i
A
− βo
Podemos llegar al mismo resultado considerando que G m = o = o = I =
v b ii Ri Ri (1 + R L Go ) rbe
−
Resumen de parámetros de la configuración emisor común (EC)
Ri =
vb
= rbe
ib
Ro =
1
Go
βo
il
=−
1 + RL Go
ib
β o RL
v
Rm = o = −
1 + Go RL
ib
AI =
AV =
β o RL
vo
=−
vb
rbe (1 + Go R L )
βo
i
Gm = l −
v b rbe (1 + R L G o )
Configuración de colector común
ic
ib
RS
Vcc
R1
R2
RB
Ri’ Ri
+
vBE -
+
vCE
-
RL
Ro’
Ro
vO
is
+ vbe
ib - rbe
RS
ic
RL
Ri’
si Go → 0 ⇒ Ri ≈ rbe + R L ( β o + 1)
Ri
Fig. 4.10. Configuración de colector común
RL
ib ( β o + 1)
1 + Go R L
RL
( β o + 1)
luego Ri = rbe +
1 + Go R L
+
GO
RB
β o ib
pero vb = ib rbe +
vo
≡≡
vs
v
a) Ri = b
ib
+
vce
-
≡
vs
vs
iC
iB
RS
+
vbe -
vo
il
vce
RL
_
Ro
75
(reflexión de RL del emisor a la base)
vs
= Ri || R B + R S
is
i
i (β + 1)
b) AI = l , pero il = ib (β o + 1) − v o G o = i b (β o + 1) − il R L G o ⇒ il = b o
1 + R L Go
ib
(β o + 1)
entonces AI =
1 + R L Go
i
RB
AIS = l , pero ib = i s
R B + Ri
is
(β o + 1) R B
i
i i
i
entonces AIS = l = l b = AI b =
i s ib i s
i s 1 + R L G o Ri + R B
RB
(β o + 1)
si Go → 0 ⇒ AI ≈ (β o + 1) ; AIS =
Ri + R B
vo
RL
RL
ib (β o + 1) y vb = ib rbe + v o = ib rbe +
ib (β o + 1)
c) A V =
, vo =
1 + Go RL
1 + Go R L
vb
RL
ib (β o + 1)
1 + Go R L
vo
R L (β o + 1)
entonces AV =
=
=
RL
vb
r (1 + Go R L ) + R L (β o + 1)
ib rbe +
i b (β o + 1) be
1 + Go R L
RL
R + Ri
v s = i s R S + v b = ib B
R S + i b rbe +
ib (β o + 1)
1 + Go R L
RB
RL
RL
(β o + 1)ib
(β o + 1)
1 + Go R L
1 + Go RL
vo
entonces AVS =
=
=
R B + Ri
RL
v s  R B + Ri

RL
(β o + 1)
R S + rbe +

(β o + 1)ib
RS + rbe +
1
R
G
R
+
1
R
G
R
+
B
o
L
B
o L


Ri ' =
si Go → 0 ⇒ AV =
d) Ro =
vo
R L (β o + 1)
R L (β o + 1)
; AVS =
=
R B + Ri
v b rbe + R L (β o + 1)
RS + rbe + R L (β o + 1)
RB
v2
, si i2 = 1, entonces
i2
RS
Ib
+
vbe RB
i2
B
is
+
vce
v2
RS
ib
RBE
_
≡≡
GO
RB
β o ib
i2
Ro
Fig. 4.10. Resistencia de salida de la configuración de colector común
vce
v2
i2
+
Ro
76
v2 =
1
[ib (β F + 1) + 1] y además v 2 = −ib (rbe + RS || R B ) , entonces
Go
R S || R B + rbe 1
(β + 1)
R S || R B + rbe
v2
(β o + 1) Go
1
v2 = − o
+
⇒ v2 =
=
1
Go R S || R B + rbe G o
G o (R S || R B + rbe ) + (β o + 1) R S || R B + rbe
+
Go
(β o + 1)
entonces
R S || R B + rbe 1
||
|| R
(β o + 1) Go L
rbe
rbe
|| R
si Go → 0 y R S || R B << rbe ⇒ Ro ≈
y Ro ' ≈
(β o + 1)
(β o + 1) L
ib (β o + 1)R L
(β + 1)R L
1 + Go R L
v
e) Transresistencia R m = o =
⇒ Rm = o
1 + Go RL
ib
ib
(β o + 1)ib
1 + RL Go
i
(β o + 1)
h) Transconductancia G m = l =
=
vb

R (β + 1)  rbe (1 + R L G o ) + R L (β o + 1)

ib  rbe + L o
1 + R L G o 

Ro =
R S || R B + rbe 1
||
(β o + 1) Go
Ro ' =
Resumen de parámetros de la configuración colector común (CC)
vb
RL
( β o + 1) ≈ rbe + R L ( β o + 1)
= rbe +
1 + Go R L
ib
v
R L (β o + 1)
R L (β o + 1)
AV = l =
≈
v b rbe (1 + Go R L ) + R L (β o + 1) rbe + R L (β o + 1)
R || R B + rbe 1
rbe
||
Ro = S
≈
(β o + 1) Go (β o + 1)
Ri =
v o (β o + 1)R L
=
1 + Go RL
ib
i
(β o + 1)
Gm = l =
v b rbe (1 + R L G o ) + R L (β o + 1)
Rm =
Configuración de base común (BC)
a) Ri =
ve
pero v e = −ib (rbe + R B )
ie
e ie = −(β o + 1)ib , entonces
rbe + R B
βo +1
v
R E (rbe + R B )
Ri ' = e = Ri || R E =
is
rbe + R B + R E (β o + 1)
Ri =
AI =
(β o + 1)
il
=
≈ (β o + 1)
ib 1 + R L G o
77
il
ie
b) AI =
βo
βo + 1
r + RB
i
AIS = l , pero i ' R E = −ib (rbe + R B ) ⇒ i ' = −i b be
is
RE
pero, il = − β o ib e i e = −(β o + 1)ib , luego AI =
 rbe + R B

+ (β o + 1)
 RE

β o RE
il
− β o ib
entonces AIS = =
=
is
 r + RB
 rbe + R B + R E (β o + 1)
− ib  be
+ (β o + 1)
 RE

βo
si R E (β o + 1) >> R B + rbe , entonces AIS ≈
(β o + 1)
e i s = i '+i e = i '−(β o + 1)i b = −i b 
E
RS
Vcc
RE
ib
ic C
B
vo
RL
RB
RL
R1
+
vBE
iC
+
vCE
-RE
Ri’ Ri
vO
≡≡
Ro’
Ro
≡
iB
R2
vs
ie - v +
ce
vbe +
RS
is
Go = 0
vs
vs
ic C
ie E
RS
i’
RBE
β O IB
RE
ib
RB
B
il
RL
Ro’
Ro
Ri
Ri’
vo
Fig. 4.11. Configuración de base común
β o RL
− β o ib R L
vo
il R L
,
=
=
=
v e − ib (rbe + R B ) − ib (rbe + R B ) rbe + R B
R
podemos comprobar que AV = AI L
Ri
β o RL
v
v v
Ri '
AVS = o = o e =
v s v e v s rbe + R B Ri '+ R S
d)
AV =
e) R o =
v2
→∞
i2
Go = 0
RS
ic C
ie E
i’
RBE
β O IB
RE
ib
RB
B
v2
i2
Ro
Fig. 12. Resistencia de salida de la
configuración de base común
78
β R
vo
− ib β o R L
=
⇒ Rm = o L
β o +1
i e − i b (β o + 1)
βo
i
− β o ib
g) Transconductancia G m = l =
=
v e − ib (rbe + R B ) rbe + R B
f) Transresistencia R m =
Tarea: Plantear sistema de ecuaciones para Go ≠ 0
Resumen de parámetros de la configuración base común (BC)
βo
il
=
ie β o + 1
v
Ro = 2 → ∞
i2
v e rbe + R B
=
βo +1
ie
β o RL
v
AV = o =
v e rbe + R B
Ri =
Rm =
AI =
vo β o RL R E
=
ie
rbe + R B
Gm =
βo
il
=
v e rbe + R B
Configuración de emisor común (EC) con resistencia de emisor
Vcc
Go = 0
R1
iB
RS
R2
vs
is
RL
+
vBE
iC
+
vCE
--
ib
RS
+ vbe
vO
≡≡
vs
ic
rbe
+
vce
β o ib _
-
RB
RE
RE
Ri
Ro
Fig. 4.13. Configuración de emisor común con resitencia de emisor
v b ib (rbe + R E (β o + 1))
=
= rbe + R E (β o + 1)
ib
ib
i
b) AI = l = − β o
ib
β o RL
v
− ib β o R L
c) AV = o =
=−
v b ib (rbe + R E (β o + 1))
rbe + R E (β o + 1)
a)
Ri =
d) Ro → ∞ , ya que al desconectar la carga, vemos la fuente de corriente ideal β o ib.
v o − ib β o R L
=
⇒ Rm = − β o RL
ib
ib
βo
i
− β o ib
f) Transconductancia G m = l =
=−
v b ib [rbe + R E (β o + 1)]
rbe + R E (β o + 1)
e) Transresistencia R m =
vo
il
RL
79
Rectas de carga de DC y AC
Al plantear la ecuación de mallas en el puerto de salida, utilizamos el concepto de recta de carga, concepto que
fué sumamente útil para el estudio de la polarización. Si a uno de los circuitos como los estudiados se le conecta una
carga acoplada mediante un condensador, tendremos una resistencia de carga para DC y otra para AC. En el circuito
de la figura 4.14 se muestra una configuración que da lugar a dos circuitos equivalentes, uno para DC y otro para
AC; una de sus diferencias estriba en la carga. De esta forma, la recta de carga variará dependiendo si hacemos el
análisis en AC o en DC.
vO
Vcc
RS
vs
R2
iB
+
vBE
iC
+
vCE
--
+
vbe
R2
vs
RC
R1
Ib
RS
iC
+
vce
--
RL ||RC
RE
vO
b)
≡≡
VO
RL
RE
RB
VBB
a)
IB
+
VBE -
IC
RC
+
VCE
RE
c)
Fig. 4.14. a) Amplificador con BJT y carga acoplada por capacitor. b) Circuito
equivalente para el análisis AC c) para el análisis DC
Si analizamos el circuito de la figura 4.14c), tenemos que la recta de carga de salida está dada por
I C (RC + R E ) + I B R E + VCE − VCC = 0
IC ≅ β F I B
si, por simplicidad tomamos
entonces

 β + 1 
 + VCE − VCC = 0
I C  RC + RE  F
 β F 

podemos definir una recta de carga de DC Rdc como
 β + 1

Rdc = RC + RE  F
 βF 
y la recta de carga de salida de corriente directa se puede expresarse de la siguiente manera
I C Rdc + VCE − VCC = 0
VCC
80
iC
Recta de carga de AC
Q
Recta de carga de DC
vCE
Fig. 4.15. Rectas de carga de AC y DC
Para analizar el circuito de la figura 4.14c), sustituimos el transistor por su modelo equivalente, resultando
is
ib
RS
+ vbe
vs
ic
Go = 0
rbe
+
vce
β o ib _
-
RB
RE
vo
RL
RC
+
ve
_
Fig. 4.16. Análisis de pequeña señal de un amplificador con BJT con carga
acoplada por capacitor usando el modelo de pequeña señal de BJT

β +1 
v ce = v o − v e = −i c (RC || R L ) − ib (β o + 1)R E = −i c  RC || R L + o
R E 
βo



β +1 
v ce + i c  RC || R L + o
R E  = 0
entonces
β
o


y definimos la recta de carga de AC Rac , como R ac = RC || R L +
βo +1
RE
βo
Circuitos con FETs
Para hacer el analisis de pequeña señal de los circuitos con FETs, utilizaremos dispositivos MOSFET
incrementales; debido a que el circuito equivalente de pequeña señal de los JFETs, los MESFETs y los MOSFETs
decrementales son idénticas a las de aquel, lo que aqui concluyamos se aplica también a circuitos que incluyan estos
dispositivos.
81
Configuraciones
VDD
VDD
iG
vs
+
vGS
RB
_
RD
RA
RD
RA
vo
iD
+
vDS
_
iG
vs
+
vGS
_
RB
RS
VDD
RD
RA
iD
+
vDS
_
iG
+
vGS
vo
_
RB
RS
vs
RS
b)
a)
vo
iD
+
vDS
_
c)
4.17. Configuraciones de circuitos con FETs a) surtidor común b) drenador común c) puerta común
Analizaremos las configuraciones de las figuras 4.17a) y b) simultáneamente, considerando la siguiente
configuración general. La configuración de la figura 4.17a) se analiza incluyendo una resistencia de surtidor
(surtidor común con resistencia de surtidor) y la de la figura 4.17b) con una resistencia de drenador (drenador
común con resistencia de drenador). Este es el caso general, de ir el surtidor o el drenador a tierra, basta con igualar
RS o RD en las expresiones resultantes.
VDD
RD
RA
iG
vs
+
vGS
RB
_
iD
+
vDS
_
D
vo1
≡
is
vo2
G
vs
RS
id
gmvgs
+ vgs
RB
-
RS
+
vo2
_
+
RDS vds
_
S
vo1
RD
Fig. 4.18. Análisis de pequeña señal de las configuraciones surtidor común y drenador común
Para las configuraciones de surtidor común (tomando vo1 como salida) y drenador común (tomando vo2 como
salida).
Configuración de surtidor común con resistencia de surtidor
De la figura 4.17a podemos deducir:
vs
= RB
is
i
b) AI = d . Sabemos que vo1 = −id R D = i d R S + rds (id − g m v gs ), entonces
is
a)
Ri =
82
id =
µ v gs
RS + RD + rds
con µ = g m rds ,
por lo tanto v s = i s R B = v gs + R S i d = i d
R S + R D + rds
i s µ RB
, luego
+ RS id ⇒ id =
µ
R S (µ + 1) + R D + rds
µR B
id
.
=
i s R S (µ + 1) + R D + rds
− i s µR B
v
c) AV = o1 . Pero v o1 = −i d R D =
RD ,
vs
R S (µ + 1) + R D + rds
además v s = i s R B ,
v
µR D
entonces AV = o1 = −
vs
RS (µ + 1) + RD + rds
v
d) Ro = 2 , si i2 = 1 A Ro = v 2 , entonces
i2
v 2 = RS + rds (1 − g m v gs ), pero v gs = − RS , entonces
AI =
Ro = RS (µ + 1) + rds
−
D
G
gmvgs
+ vgs
-
+
RDS vds
_
S
Fig. 4.19. Cálculo de la resistencia de salida de
la configuración de la figura 4.18
µR B i s
RD
RS (µ + 1) + R D + rds
µR D R B
.
=−
is
R S (µ + 1) + R D + rds
Configuración de drenador común con resistencia de drenador
Observando la figura 4.17b, tenemos que
vs
= RB
is
D
µRB
i
b) AI = d =
+
is RS (µ + 1) + RD + rds
gmvgs
RDS vds
G
µ v s RS
v
_
S
c) AV = o 2 , pero vo 2 = i d R S =
, luego
v
RD
vs
RS (µ + 1) + R D + rds
2
+ vgs µR S
i2
AV =
R S (µ + 1) + R D + rds
v
d) Ro = 2 , si i2 = 1 A Ro = v 2 , entonces
i2
Fig. 4.19. Cálculo de la resistencia de salida de la
a)
Ri =
(
)
v 2 = −v gs = R D + rds 1 + g m v gs , entonces
Ro =
R D + rds
(µ + 1)
i2
RS
v o1
v
−i R
Rm = o1 = d D =
is
is
is
µ is RB
−
i
R S (µ + 1) + R D + rds
−i
µ
f) G m = l = d =
=−
vs
vs
is RB
R S (µ + 1) + R D + rds
e) Rm =
v2
configuración de la figura 4.17b.
83
µ v s RS
µ RS R B
v
i R
R (µ + 1) + R D + rds
v
e) Rm = o 2 Rm = o 2 = d S = S
=
v
v
is
R S (µ + 1) + R D + rds
is
s
s
RB
RB
µ vs
(
−i
i
R µ + 1) + R D + rds
µ
f) Gm = l = d = S
=−
vs
vs
vs
R S (µ + 1) + R D + rds
Configuración de puerta común
A continuación reproducimos la figura 4.17c, que representa la configuración de puerta común
VDD
D
RD
RA
iG
+
vGS
RB
id
_
iD
+
vDS
_
vo
gmvgs
G
≡
+
RDS vds
_
S
+ vgs
RB
-
vo3
il
RD
is
RS
vs
RS
Fig. 4.20. Configuración de puerta común
a)
Ri =
v s = −i d
vs
. Sabemos que v s + rds (i d − g m v gs ) = −id R D ⇒ v s + i d (rds + R D ) = µ v gs , entonces
is

(RS + R D )i s rds
v (µ + 1) 
rds + RD
 ⇒ v s =
. Además v s = R S (i s + i d ) = R S  i s − s
, luego
µ +1
µ
1
r
R
R
R
r
(
)
+
+
+
+
S
D
ds
ds
D 

vs
R S (R D + rds )
=
= RS
is
R S (µ + 1) + R D + rds
R +r 
||  D ds  .
 µ +1 
µ +1
− vs
i
i
R D + rds
(µ + 1)RS
D
b) AI = l = − d = −
=
v s (RS (µ + 1) + R D + rds ) RS (µ + 1) + R D + rds
is
is
v2
+
RS (R D + rds )
gmvgs
RDS vds
G
v o3
_
c) AV =
, pero v o 3 = −i d R D , entonces
vs
S
i2
+ vgs − id RD
(µ + 1)R D
AV =
=
RB
rds + R D
rds + R D
− id
µ +1
v
d) Ro = 2 , si i2 = 1 A, Ro = v 2 , entonces
i2
Fig. 4.21. Cálculo de la resistencia de salida de
Ri =
la configuración de la figura 4.20.
84
v 2 = rds (1 − g m v gs ) = rds , entonces
Ro = rds
µ +1
RD
vo − id R D
R D + rds
(µ + 1)RS R D
g) Rm =
=
=
=
v s (RS (µ + 1) + R D + rds ) R S (µ + 1) + R D + R S
is
is
R S (R D + rds )
(µ + 1)v s
i
R + rds
−i
(µ + 1)
Gm = l = d = D
=
vs
vs
vs
R D + rds
− vs
Amplificadores de transistores en cascada
Para algunas aplicaciones, los requerimientos de amplificación son mayores a los que podríamos obtener con un
solo amplificador; en esos casos, es necesario conectar en cascada dos o más amplificadores. Otra situación en que
es necesario el encadenamiento de amplificadores es cuando la impedancia de entrada y/o salida de un solo
amplificador no sean adecuadas para una aplicación particular. Supongamos que deseamos un amplificar en voltaje
una señal proveniente de un micrófono, que produce una señal de baja amplitud y tiene poca capacidad para
suministrar potencia. Como queremos un amplificador de voltaje, deseamos que la resistencia de entrada sea
grande, de tal forma que no “carge” al micrófono, y una baja resistencia de salida. Las siguientes son las
posibilidades de que disponemos en caso que queramos usar amplificadores construidos con BJTs, en función de la
resistencia de entrada.
ƒ
Emisor común: Ri baja
ƒ
Colector común: Ri alta
ƒ
Base común: Ri baja
ƒ
Emisor común con resistencia de emisor : Ri alta,
por lo tanto, debemos seleccionar entre las configuraciones de colector común y emisor común con resistencia de
emisor. Sin embargo, la configuración de colector común no puede suministrar una ganancia de tensión mayor de 1,
por lo que seleccionamos la configuración de emisor común con resistencia de emisor como primera etapa.
Aún nos queda por resolver el problema de la resistencia de salida, ya que la primera etapa que seleccionamos
(emisor común con resistencia de emisor) presenta una alta resistencia de salida. Por lo tanto, debemos acoplar una
segunda etapa, que sea al menos comparable con la resistencia de salida de la primera etapa, y proporcione una baja
resistencia de salida. Esta etapa es un colector común, que tiene una alta resistencia de entrada y una baja resistencia
de salida; aunque no produce ganancia de tensión, esta labor se la dejamos a la primera etapa. Con la combinación
en cascada de una etapa de emisor común con resistencia de emisor y una etapa de colector común, logramos
obtener el amplificador deseado.
Cuando estudiamos los diferentes tipos de amplificadores, vimos que dependiendo de la característica física que
queramos amplificador (voltaje, corriente, transresistencia o transconductancia), pudimos observar que cada tipo
tiene características particulares. Por ejemplo, un amplificador de voltaje debia tener alta impedancia de entrada y
baja impedancia de salida, y por supuesto, ganancia de voltaje mayor que uno; de igual forma un amplificador de
corriente debia tener baja impedancia de entrada, alta impedancia de salida y ganancia de corriente mayor que uno.
Luego, podemos comparar las configuraciones de amplificadores con BJTs en función de sus características, y
determinar así para qué son utiles cada una de ellas.
Comparación de configuraciones de amplificadores con BJTs
EC:
ƒ
Ganancia de corriente y de tensión mayor que la unidad (AI , AV > 1).
85
ƒ
Transconductancia y transresistencia altas
ƒ
Baja resistencia de entrada (Ri baja)
ƒ
Alta resistencia de salida (Ro alta)
CC:
ƒ
Ganancia de corriente alta, ganancia de tensión menor que la unidad (AI > 1, AV < 1).
ƒ
Transresistencia alta y transconductancia baja
ƒ
Alta resistencia de entrada (Ri alta)
ƒ
Baja resistencia de salida (Ro baja)
Comentario: Este circuito encuentra gran aplicación como etapa intermedia entre una fuente de gran impedancia y
una carga de impedancia baja (amplificador de corriente). Generalmente se usa como etapa final, conteniendo la
carga que se desea atacar, que generalmente es de baja impedancia (carga elevada).
BC:
ƒ
Ganancia de tensión alta (igual a la de EC), ganancia de corriente menor que la unidad (AI < 1, AV > 1).
ƒ
Transresistencia y transconductancia altas
ƒ
Alta resistencia de entrada (Ri baja)
ƒ
Alta resistencia de salida (Ro alta)
Comentario: Esta configuración tiene pocas aplicaciones. Algunas veces se emplea para acoplar una fuente de baja
impedancia atacando una carga de gran impedancia (amplificador de transresistencia) o como fuente de corriente.
EC con RE:
ƒ
Ganancia de corriente mayor que la unidad y ganancia de tensión posiblemente mayor que la unidad (AI , AV >
1).
ƒ
Transresistencia alta y transconductancia baja
ƒ
Alta resistencia de entrada (Ri alta)
ƒ
Alta resistencia de salida (Ro alta)
Comentario: Su ganancia de tensión es muy estable y practicamente independiente de cualquier parámetro del
transistor. Generalmente se usa como etapa amplificadora de voltaje inicial o intermedia, pero no como etapa final,
pues no es capaz de atacar una carga de baja impedancia.
Podemos observar que generalmente las configuraciones no se comportan por si solas en forma simular a un
amplificador ideal. Por ejemplo, la configuración de emisor común con resistencia de emisor tiene una impedancia
de entrada alta, por lo que no se comporta como un amplificador de corriente o de transresistencia ideal, además, su
resistencia de salida es alta, por lo tanto no puede ser similar un amplificador de tensión ideal; la única posibilidad
que resta es que sea un amplificador de transconductancia, pero su transconductancia es menor que la unidad.
Comparación de configuraciones de amplificadores con FETs
SC:
ƒ
Ganancia de tensión mayor que la unidad (AV > 1).
ƒ
Transconductancia baja
ƒ
Resistencia de entrada alta (Ri alta)
ƒ
Alta resistencia de salida (Ro alta)
Comentario: Análoga a la configuración EC con RE.
86
DC:
ƒ
Ganancia de tensión menor que la unidad (AV < 1).
ƒ
Transconductancia baja
ƒ
Resistencia de entrada infinita (Ri → ∞)
ƒ
Baja resistencia de salida (Ro baja)
Comentario: Análoga a la configuración CC.
PC:
ƒ
Ganancia de tensión alta (igual a la de EC), ganancia de corriente menor que la unidad (AI < 1, AV > 1).
ƒ
Transresistencia baja y transconductancia alta
ƒ
Baja resistencia de entrada (Ri baja)
ƒ
Alta resistencia de salida (Ro alta)
Comentario: Esta configuración tiene pocas aplicaciones, debido a que carece de la principal ventaja de los
amplificadores con FETs, que es su muy alta resistencia de entrada, que permite conectarlos a cualquier circuito
adicionando una carga mínima a la fuente de señal. Análoga a la configuración BC.
Algunas configuraciones se aproximan mejor a un amplificador ideal; por ejemplo, un amplificador construido
con una configuración de colector común tiene una resistencia de entrada baja, una resistencia de salida baja y una
transresistencia alta, lo que lo aproxima a un amplificador de transresistencia. Sin embargo, generalmente para
cumplir con la mayoria de los requerimientos prácticos, se conectan los amplificadores en cascada.
Al conectar los amplificadores en cascada, la salida de uno de ellos se conecta a la entrada de la siguiente.
is RS
il
RI1 Etapa I RO1
vs
+
RL vl
_
RI1 Etapa II RO2
Fig. 4.22. Circuito equivalente de amplificadores en cascada
Ejemplo
Vcc
v2
RC1
R1
iB1
RS
vs
R2
+
vBE1 -
iC1
+
vCE1
RE1
iB2
+
vBE2
iC2
+
≡≡
vCE2
vs
vO
RE2
v1
RS
RB1
Ri1’
-
ib1
+
vbe
ie1
1
ic2
ic1
+
vce1
-
ib2
RE1
RC1
+
vbe2
Ri2
Ri1
Ro1
ie2
Ro2
+
vce2
vo
RE2
Ro2’
87
Ecuaciones aproximadas para amplificadores con BJTs (GoRL <<1)
BC
rbe
rbe + R E (β o + 1)
CC
Ri
EC
rbe + R L ( β o + 1)
AI
− βo
− βo
βo +1
rbe + RB
βo +1
βo
βo +1
AV
−
EC con RE
β o RL
rbe
−
β o RL
R L (β o + 1)
β o RL
rbe + R E (β o + 1) rbe + R L (β o + 1) rbe + RB
Ro
∞
∞
Rm
− β o RL
− β o RL
Gm
−
βo
rbe
−
RS || R B + rbe
(β o + 1)
∞
(β o + 1)RL
(β o + 1)
βo
rbe + R E (β o + 1) rbe + R L (β o + 1)
β o R L RE
rbe + R B
βo
rbe + RB
Ecuaciones aproximadas para amplificadores con FETs
SC con RS
DC con RD
Ri
RB
RB
PC
R S (R D + rds )
R S (µ + 1) + R D + rds
AI
µR B
RS (µ + 1) + R D + rds
µR B
RS (µ + 1) + R D + rds
(µ + 1)RS
RS (µ + 1) + RD + rds
AV
−
R S (µ + 1) + rds
Ro
Rm
Gm
µR D
µR S
R S (µ + 1) + R D + rds RS (µ + 1) + R D + rds
−
µR D R B
R S (µ + 1) + R D + rds
−
µ
R S (µ + 1) + R D + rds
RD + rds
(µ + 1)
µ RS RB
RS (µ + 1) + R D + rds
−
µ
RS (µ + 1) + R D + rds
(µ + 1)R D
rds + R D
rds
(µ + 1)RS RD
RS (µ + 1) + RD + RS
(µ + 1)
RD + rds
88
Supongamos que Go → 0
a)
Ri1 = rbe1 + R E1 (β o1 + 1) , Ri1 = rbe 2 + R E 2 (β o 2 + 1)
b)
AI =
c)
i e 2 ie 2 ib 2 ic1
i
RC 1
, entonces
=
= AI 1 b 2 AI 2 , pero ib 2 = −ic1
ib1 ib 2 i c1 ib1
i c1
RC 1 + Ri 2
AI = −
RC 1
AI 1 AI 2 , pero AI 1 = β o1 y AI 2 = (β o 2 + 1) , luego
RC1 + Ri 2
AI = −
RC1 β o1 (β o 2 + 1)
R C1 + R i 2
AV =
v
v v
Ri1
vo vo v2
v
=
= AV 1 AV 2 , y AVS = o = o 1 = AV 1 = AV
v1 v 2 v1
v s v1 v s
vs
Ri1 + R S
Hallemos AV1 y AV2 .
AV 1 =
v 2 − i c1 RC1 || Ri 2 − β o1 RC1 || [rbe 2 + R E 2 (β o 2 + 1)]
=
=
v1
i b1 Ri1
rbe1 + R E1 (β o1 + 1)
AV 2 =
(β o 2 + 1)RE 2
v o ie 2 R E 2
, luego
=
=
v 2 ib 2 Ri 2 rbe 2 + R E 2 (β o 2 + 1)
AV =
vo
− β o1 (β o 2 + 1)(RC1 || Ri 2 )R E 2
. Note que obtendríamos el mismo resultado si
= AV 1 AV 2 =
v1
Ri1 Ri 2
AV = AI
RL
R
− β o1 (β o 2 + 1)RC1 R E 2 − β o1 (β o 2 + 1)(RC1 || Ri 2 ) R E 2
.
= AI E 2 =
=
Ri
Ri1
R C1 + R i 2
Ri1
Ri 2
Ri1
Esta última relación debe usarse cuidadosamente. Al relacionar la ganancia de tensión con la ganancia de
corriente y la resistencia de entrada, estamos relacionando UNA DETERMINADA ganancia de tensión con
DETERMINADAS ganancia de corriente y resistencia de entrada; si usamos una ganancia de corriente o una
resistencia de entrada que no equivocada, obtendremos un resultado erróneo. En nuestro ejemplo, la ganancia de
tensión AV está relacionada con AI y con Ri1, ya que
AV =
vo ie 2 RE 2
R
=
= AI E 2 ,
v1 ib1 Ri1
Ri1
si usaramos Ri2 en lugar de Ri1, obtendríamos un resultado erróneo.
d)
Ro1 = ∞ ,
Ro 2 =
rbe 2 + RC1
β o2 + 1
y
Ro 2 ' =
rbe 2 + RC1
|| R E 2 .
β o2 + 1
89
ANÁLISIS DE POTENCIA EN CIRCUITOS CON DISPOSITIVOS DE TRES TERMINALES
Conceptos fundamentales
ƒ
Potencia instantánea: p (t ) = v(t ) ⋅ i (t )
ƒ
Potencia promedio: P =
1
T
∫
T
p(t )dt .
Para una onda sinusoidal P = V m I m cos θ , donde
Vm : valor máximo (pico) de la señal de voltaje
Im : valor máximo (pico) de la señal de corriente
Si el elemento que disipa esta potencia es una resistencia pura
P=
Vm I m
2
Note que a pesar que el valor promedio de una señal senoidal es cero, la potencia promedio es distinta de cero.
Como es útil comparar la potencia que entrega una fuente de una señal AC en comparación con una fuente de señal
DC, se ha definido el valor efectivo.
ƒ
Valor efectivo (eficaz): E =
1
T
∫
T
E 2 (t ) dt
El valor efectivo de voltaje que suministra una fuente de señal AC es una medida de su efectividad para
entregar potencia a un resistor de carga. El concepto proviene del deseo de tener un voltaje (o una corriente) AC que
entregue a un resistor de carga la misma potencia que un voltaje (o una corriente) DC.
Para una onda senoidal:
I eff =
Im
2
,
Veff =
Vm
2
y
2
P = I eff R L =
Veff
2
RL
Distorsión:
Generalmente la característica de transferencia dinámica (iC
en función de iB) no es una línea recta. Ya hemos visto que βF
varía con el punto de trabajo. Esta no linealidad se puede
visualizar en la característica de salida del dispositivo.
Podemos observar que las curvas parametrizadas no son
equidistantes para iguales incrementos de la excitación de
entrada, lo que se conoce como distorsión no lineal o de
amplitud.
Cualquier sistema puede ser tratado analíticamente en
forma lineal para pequeñas variaciones del punto de reposo,
pero en amplificadores de potencia la señal de salida es
grande, por lo que debe tenerse en cuenta la curva de
transferencia completa.
iC
βF
iB
Fig. 5.1. Característica de transferencia de corriente
típica de un amplificador de potencia
90
Señal de entrada
Señal de salida
Señal distorsionada
Sistema
t
t
Señal sin distorsión
Fig. 5.2. Distorsión de forma de onda en un amplificador de potencia
Distorsión armónica
Para una función de transferencia no lineal, en particular para una respuesta parabólica,
2
ic = G1ib + G 2 ib .
Si ib = I bm cos ω t , entonces
i c = G1 I bm cos ω t + G 2 I bm (cos ω t )
1 + cos 2ω t
,
(cos ω t )2 =
2
iC = I C + i c = I C + Bo + B1 cos ω t + B2 cos 2ω t .
2
pero
2
luego
Las componentes de mayor frecuencia (armonicos de orden superior) causan distorsión de la señal. A medida que
se añaden armónicos, aumenta la distorsión; sin embargo, la magnitud de los armónicos disminuye
exponencialmente con la frecuencia o el orden del armónico, así que para cierto orden la influencia de los
armónicos se puede obviar. De lo anterior podemos también concluir que la mayor distorsión la causará el primer
armónico, y por lo tanto, si podemos medir su magnitud, podemos tener una idea del grado de distorsión. La
distorsión de segundo armónico se define como
D2 =
B2
B1
que es la razón entre la magnitud de la fundamental y la del primer armónico. En general, una función de
transferencia no lineal (no parabólica), la podemos modelar como
2
3
4
ic = G1ib + G2 ib + G3 ib + G4 ib
⇒ iC = I C + ic = I C + Bo + B1 cos ω t + B2 cos 2ω t + B3 cos 3ω t + B4 cos 4ω t
con D 2 =
B2
B1
, D3 =
B3
B1
, D4 =
B4
B1
, ..., Di =
Bi
B1
, siendo Di la distorsión de la iésima armónica
2
y la potencia suministrada o disipada en la frecuencia fundamental es P1 =
B1 R L
2
Eficiencia
La eficiencia nos permite evaluar la idoneidad del dispositivo activo para convertir la potencia en continua de la
fuente DC en una potencia alterna cedida a la carga. Se define como
η=
Potencia entregada a la carga (AC)
x100 %
Potencia entregada al circuito (CC)
o lo que es lo mismo, la razón entre la potencia entregada por la red de alimentación o polarización (DC) al circuito
y la potencia que este es capaz de entregarle a la carga en forma de señal (AC).
91
Configuración de salida con polarización lineal (circuito tipo A)
VBB polariza al transistor en la mitad de su región activa. Su salida es una copia lineal de la señal de entrada y el
transistor se conserva polarizado en la región activa en todo momento. Si la red de polarización se diseña para
máxima excursión simétrica, V L ≈
través de la carga es v L (t ) =
entonces
VCC
. Si vs desarrolla una señal de magnitud vl en la carga, el voltaje total a
2
VCC
+ Vo sen (ω t )
2
V
V
i L (t ) = CC + o sen (ω t )
2RL RL
Polarización
señal
Vcc
R1
iC
vin
RS
vs
iB
+
vbe -
+
vCE
_
iL
R2
vO
+
RL vL
_
VBB
Fig. 5.3. Amplificador de potencia tipo A
2
luego
2
por lo tanto
2
V
V
V V
V V
p L (t ) = v L (t ) ⋅ i L (t ) = CC + CC o sen (ω t ) + CC o sen (ω t ) + o sen 2 (ω t )
4RL
2RL
2RL
RL
2
V
V
p L (t ) = CC + 0 + o , ya que 1 ∫T sen 2 (ω t )dt = 1 .
2
T
4 RL
2 RL
Polarización
señal
La potencia disipada por el transistor será
pQ (t ) = vCE (t ) ⋅ iC (t ) ≈ vCE (t ) ⋅ i L (t )
pero
VCC
− Vo sen (ω t )
2
2
2
2
2
VCC
Vo
VCC
Vo
2
−
−
sen (ω t ) ⇒ PQ = p Q (t ) =
p Q (t ) =
.
4RL
4R L 2 RL
RL
vCE (t ) = VCC − v L (t ) =
entonces
El signo negativo del componente de señal indica que la potencia promedio en el tiempo disipada en el transistor
se reduce cuando el punto de trabajo se desplaza del punto de polarización, ya que aumenta vCE pero disminuye iC, y
viceversa.
La potencia que se toma de la fuente de alimentación en el puerto de entrada es generalmente mucho menor que la
que se toma en el puerto de salida, así que la potencia que se toma de la fuente de alimentación en el puerto de
salida es aproximadamente igual a:
92
entonces
V

V
p S (t ) = VCC ⋅ iC (t ) ≈ VCC ⋅ i L (t ) = VCC ⋅  CC + o sen (ω t )
 2RL RL

2
V
PS = p S (t ) = CC ,
2RL
note que
p S (t ) = p L (t ) + p Q (t )
2
y la eficiencia estará dada por
η=
p L (t )
p S (t )
=
Vo
2RL
=
2
VCC
2RL
Vo
2
VCC
2
si el circuito se ha polarizado para máxima excursión simétrica Vo ≈
VCC
, entonces
2
2
 VCC 


 2 
η=
= 25%
2
VCC
siendo generalmente menor que este porcentaje, debido a la potencia disipada en la entrada, que no hemos
considerado.
Configuración de salida de par complementario (amplificador tipo B)
Cuando un amplificador debe entregar grandes corrientes de carga, es deseable polarizarlo de tal forma que el
voltaje de salida sea próximo a cero, para poder así reducir la potencia disipada en ausencia de señal, tanto en la
carga como en los dispositivos activos de la etapa de salida. Si el amplificador se alimenta con fuentes bipolares, el
voltaje de salida excursionará en los ciclos positivos y negativos de la señal AC. Esta configuración de potencia se
conoce como el par complementario, configuración de seguidor en contrafas (push-pull) o amplificador clase B.
Los amplificadores clase B se pueden elaborar con MOSFETs o JFETs. La fuente de señal vs y la resistencia RS
representan el voltaje y la resistencia de salida de la etapa anterior. Si RS es pequeña, entonces vi ≈ vs . En el
amplificador clase B, ninguno de los dispositivos está polarizado en la región activa. Cuando la señal de entrada es
positiva, lleva al dispositivo superior (Q1) a la región activa, mientras el inferior (Q2) se mantiene en corte. De igual
manera, cuando la señal de entrada es negativa (semiciclo negativo), el dispositivo inferior (Q2) opera en la región
activa, mientras que el superior (Q1) está en corte.
93
iC1
iC
vCE2
Q1 Q2
t
t
vCE1
vi
iC2
Fig. 5.4. Característica de salida de un amplificador tipo B
Vcc
iC1
+
vCE1 Q1
iL
iB1
RB
+
vBE1 -
vi
vL
vEB2
vs
+
vCE2 Q2
+
iB2
Carga
iC2
-VEE
Vcc
iB1
RB
vi
+
Vγ1 -
Fig. 5.5. Amplificador tipo B
iC1
+
vCE1 Q1
-i
vL = vi – Vγ1
L
RB
vs
vi
iL
+
vγ2
iB2
vs
Carga
vL = vi – Vγ2
vCE2 Q2
+
iC2
-VEE
Fig. 5.6. Amplificador tipo B en a) el semiciclo positivo de la señal de entrada b) el semiciclo negativo
Carga
94
Para –Vγ1 < vi < Vγ2 ambos transistores están en corte,
así que vL = 0. Cuando cualquiera de los dispositivos
está activo, la resistencia de salida de pequeña seña es
R +r
Ro = S bei , con i = 1,2.
βo +1
Q1 on y Q2 off
Sin embargo, la etapa
de salida opera bajo condiciones de gran señal, en las
que no son aplicables el modelo de pequeña señal. El
valor de rbe varia considerablemente si la señal de
salida tiene grandes excursiones. Pero, debido al que
el amplificador clase B opera la mayor parte del
tiempo cerca del corte, y que para esta zona el valor
de rbe es pequeño, podemos decir tomar la resistencia
de salida como Ro ≈
vo
Q1 y Q2 off
Q2 on y Q1 off
-Vγ
vi
Vγ
Comportamiento
no lineal
Fig. 5.7. Distorsión de cruce por cero
en un amplificador tipo B
RS
.
βo + 1
Debido a que no fluye corriente de polarización a
través de Q1 y Q2, la única potencia disipada en la carga es aquella asociada con la señal de salida. Por lo tanto
i L (t ) =
Vo
sen (ω t )
RL
2
2
V
 V
V
⇒ p L (t ) = v L (t ) ⋅ i L (t ) = Vo sen (ω t ) o sen (ω t ) = o sen 2 (ω t ) ⇒ p L (t ) = o
RL
 RL
 RL
.
Para encontrar la potencia que consume el circuito de las fuentes de alimentación, consideremos que VCC = V EE ,
por lo que calculamos el consumo en un semiciclo
p s + (t ) =
1
T
∫
T /2
0
VCC ic1(t ) dt =
1
T
∫
T /2
0
VCC
Vo
Vcc Vo
sen (ω t )dt =
π RL
RL
y la potencia en ambos semiciclos es igual a
p s (t ) = p s + (t ) + p s − (t ) =
2Vcc Vo
π RL
y la eficiencia de este tipo de amplificadores estará dada por
2
Vo
p L (t )
πV o
2RL
η=
=
=
,
p S (t ) 2VCC Vo 4VCC
πR L
si Vo = Vcc
η=
π
≈ 78.5% .
4
Se puede observar que para la misma potencia de señal senoidal, el amplificador tipo B tiene tres veces la
eficiencia del tipo A. Esta configuración no disipa potencia de polarización en la carga o en los transistores, y por lo
tanto se usa cuando la eficiencia es importante.
Amplificador clase AB
La distorsión en el punto de cruce del amplificador clase B se puede mejorar al polarizar ligeramente los
dispositivos en la región activa, justo por encima del corte. En un amplificador clase AB con BJTs, esto se puede
lograr colocando una red de polarización como la mostrada en la figura 5.8; la caida de tensión entre los terminales
de R2 mantiene a ambos transistores polarizados en la región activa aún en ausencia de la señal de entrada. El costo
95
pagado por eliminar la distorsión es una disminución en la eficiencia del amplificador, ya que la corriente de emisor
en reposo, aunque pequeña, es mayor que cero, ya la potencia consumida a la entrada aumenta considerablemente.
Polarización de amplificadores completarios tipo AB
Vcc = 30 V
R1
iB1
1
vi
R2
+
vBE1 =0.6 V 3
vEB2 = 0.6 V +
2
iB2
R3
iC1
+
vCE1 Q1
iL
vL
+ 15 V vCE2 Q2
+
RL = 10 Ω
iC2
I
Fig. 5.8. Amplificador tipo AB sin resistencia de emisor
En el esquema de polarización de un amplificador complementario, como el de la fig 5.8, se deben tener en
cuenta las siguientes consideraciones:
1. Entre los terminales del resistor R2 debe haber una diferencia de potencial que plarice en directo las uniones
base-emisor de Q1 y Q2 , así que fluye una pequeña corriente de reposo a través de los colectores, que permite
eliminar o reducir la distorsión de cruce por cero
2. Como las corriente de los emisores de Q1 y Q2 son iguales, sus corrientes de colector deben ser
aproximadamente iguales a pesar que existan diferencias en los β F de los transistores. Como I E1 = I E 2 ,
I C 1 + I B1 = I C 2 + I B 2
I C1 = I C 2 + I B 2 − I B1
o
y las corrientes de colector difieren solamente en una pequeña cantidad debida a la diferencia entre las
corrientes de base.
3. El punto 3 debe polarizarse a
VCC
= 15 V para permitir una máxima excursión simétrica del voltaje de salida.
2
4. La corriente I debe ser al menos 10 veces mayor que IB1 o IB2 para que podamos despreciar estar últimas en el
cálculo de la resistencia de polarización.
En la figura 5.9 se han encerrado en rectángulos los voltajes de polarización. Suponga que vi excursiona entre +10
V y –10 V. El punto 1 aumenta en el semiciclo positivo hasta 25.6 V. El incremento de 10 V se divide entre R2 y R3
en 0.769 V y 9.231 V respectivamente, aumentando la caida en R2 de 1.2 a 1.969 V; esta caida de potencial polariza
en directo ambos transistores, con una tensión base-emisor mayor a los 0.6 V requeridos. Además, Q2 debe estar
polarizado en inverso durante la excursión positiva de vi de tal forma que no drene corriente de la carga.
Si incluimos unas pequeñas resistencias RE1 y RE2 (generalmente de 0.47 o 1 Ω) en serie con cada emisor,
polarizaremos en inverso al unión base-emisor de Q2 (Q1) durante la excursión positiva (negativa) de la señal de
entrada. Estas resistencias también estabilizan el punto de polarización y sirven como fusibles.
En la figura 51.0, el mismo incremento de 10 V de vi produce la misma diferencia de potencial entre los puntos 1 y
2. Q1 debe conducir y ∆vi se divide enre RE1 y RL de la siguiente forma
R E1
RL
1
10
∆V RE1 = ∆vi
= 10
= 0 .9 V
y
∆V RL = ∆vi
= 10
= 9 .1 V
1 + 10
1 + 10
R E1 + R L
R E1 + R L
96
Observe que la diferencia de potencial entre los puntos 3 y 2 en la figura 5.10 es de 24.1-23.63 = 0.47 V,
insuficiente para polarizar en directo la unión B-E de Q2. El mismo análisis resulta de considerar el semiciclo
negativo de vi, en donde Q2 debe conducir y Q1 estar en corte. La caida de potencial en reposo sobre RE1 y sobre RE2
es despreciable, por ejemplo, es igual a 0.01 V para una corriente de reposo en el emisor de 10 mA y una resistencia
RE = 1Ω.
Vcc = 30 V
R1
a 25.6 V
15.6
600 Ω
1
vi
0
R2
a 10 V
50 Ω
2
iB1
+
0.6 V 3
0.6 V + + 15 V vCE2 Q2
iB2
+
R3
a 23.63 V
a 25 V
vL
RL = 10 Ω
iC2
600 Ω
14.4
iC1
+
15
vCE1 Q1
iL
I
Fig. 5.9. Amplificador tipo AB sin resistencia de emisor y señal de
entrada con excursión en el semiciclo positivo
Vcc = 30 V
15.6
600 Ω
1
vi
0
iC1
R1
a 25.6 V
R2
a 10 V
iB1
RE2=1Ω
50 Ω
2
R3
600 Ω
15
=1Ω
+ Q1 RE1
0.6 V -
iB2
iL
3
vL
+ 15 V -
Q2
RL = 10 Ω
iC2
I
14.4
a 24.1 V
a 23.63 V
Fig. 5.10. Amplificador tipo AB con resistencia de emisor
97
Circuito manejador (driver stage)
A pesar que el circuito de la figura 5.10 funciona perfectamente como una amplificador tipo AB, su resistencia de
entrada es muy baja para ser acopado directamente a un amplificador de voltaje. Por lo tanto, es conveniente
reemplazar R1 por un transistor manejador o acoplador, como el de la figura 5.11 para que funcione como un
colector común y eleve la resistencia de entrada del amplificador complementario.
Veamos como podemos diseñar esta etapa manejadora. Si la corriente
de reposo en el colector de Q3 es igual a
Vcc
I C3 ≈ I E3 = I =
VCC
30
=
= 24 mA
R1 + R 2 + R3 600 + 50 + 600
el emisor debe estar a un potencial igual a VE3 = 15 + 0.6 = 15.6 V. Para
el análisis de polarización, podemos pensar que en el emisor de Q3 existe
una resistencia RE3 = R2 + R3 = 650 Ω. Si β F3 = 100, la corriente de base
debe ser IB3 = 24 mA/100 = 240 µA. La base de Q3 está 0.6 V por encima
del emisor, o sea, a 16.2 V, así que R4 debe ser igual a
R4 =
VCC − 15.6
240 x10 − 6
R4
86.2 kΩ
IC3
IB3
Q3
+
VBE3 -
vi
= 60 kΩ
RE2
Como última modificación, podemos incluir en el circuito de la figura
5.10 un o más diodos en sustitución o combinados con R2. Esta
configuración asegura que la variación de VBE con la temperatura se
compensada, o “seguida” por los diodos.
5.11. Circuito manejador (driver stage)
Vcc = 30 V
R4
60 kΩ
iC3
iB3
iC1
iB1
Q3
Q1 RE1=1Ω
vi
iL
R2
27 Ω
iB2
R3
925 Ω
vL
RE2=1Ω
Q2
RL = 10 Ω
iC2
Fig. 5.10. Amplificador tipo AB compensado por diodo, con resistencia de
emisor y circuito manejador
98
BIBLIOGRAFÍA
ƒ Millman, Jacob. Microelectronica.McGrawHill.
ƒ Horenstein, Mark. Circuitos y dispositivos microelectrónicos. Prentice-Hall, 2da edición, 1995.
ƒ Machado, Jesús. Notas de electrónica I. No publicado.