EJEMPLOS DE CIRCUITOS MAGNÉTICOS

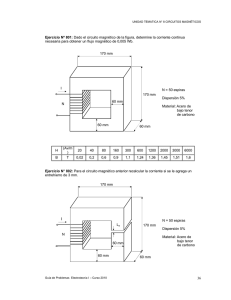
EJEMPLOS DE CIRCUITOS MAGNÉTICOS
CIRCUITOS MAGNÉTICOS
Nº 1
En el circuito de la siguiente figura, las dimensiones están dadas en centímetros,
siendo la dimensión transversal del núcleo magnético de 10 cm. La permeabilidad
relativa del material es de 3000. La corriente aplicada a cada bobinado es i1=1 A e
i2=1.5 A y el número de espiras del bobinado de la izquierda es N1=700.
Se quiere calcular el número de espiras necesario en el segundo bobinado, N2,
para que por la columna central del núcleo magnético circule un flujo de 0.05 Wb.
Resolución
Las reluctancias son combinaciones serie o paralelo de ésta.
Reluctancia genérica: lc=35 cm y Ac=50 cm2
l
0.35
0.35
1 7 Av
ℜ= c =
=
=
[
]
µA 3000 µ 0 0.005 15 µ 0 µ 0 300 Wb
φ
φ
φ
φ
φ
Según Millmann:
N1i1 N 2i2
+
N i + N 2i 2
3ℜ
3ℜ
ℑAB =
= 11
1
2
1
8
+ +
3ℜ ℜ 3ℜ
Por otra parte, se conoce que ℑAB=φℜ/2, con lo cual se obtiene que:
N 2 = 4φ
ℜ
i
− N1 1
i2
i2
N = 4 7 0.05 − 700 1 = 2009.0769 vueltas
2
450 µ
1.5
0
N2=2009 espiras
Se pueden emplear otros metodos de cálculo
CIRCUITOS MAGNÉTICOS
Nº 2
Sea el circuito magnético de la figura cuya sección transversal es de 4 cm2 y la
longitud del entrehierro 0.87 cm. La corriente aplicada al bobinado es 1 A y el número
de espiras 700. La permeabilidad relativa es 5000. Se desea calcular la magnitud del
flujo magnético que se obtiene en el entrehierro y el tanto por ciento de error que se
comete al no tener en cuenta el circuito magnético.
Resolución
Circuito magnético:
lh=2x7+5+(5-g)=24-g cm y Ah=4 cm2=0.0004 m2
lh
( 24 − g) 10−2
24 − g 5
Av
ℜh =
=
=
10
=
92031
µ hA h 5000 µ 0 410−4
8π
Wb
Entrehierro: lg=0.0087 m y Ag= (2+g)(2+g)10-4=0.00082369 m2
8.710−3
Av
ℜg =
=
=
=
8405152
µ 0A g µ 0 (2 + g) 2 10−4 8.2369 µ 0
Wb
lg
φ=
g
Ni
700
=
= 8.23810−5 Wb
ℜ h + ℜg 92301 + 8405152
Despreciando el núcleo magnético:
φ’= Ni = 700 = 8.328210−5Wb
ℜg 8405152
El error cometido:
ℜ
’
φ
−
φ
= h = 0.01095 ≈ 1.1%
ε=
ℜg
φ
Intensidad necesaria para lograr el mismo flujo sin el entrehierro
ℜt =
lt
24 10-2
=
= 159154.94 Av
µ A t µ 3000 4 10−4
Wb
o
φℜ t 8.238 10-5 ℜ t
i=
=
= 0.0187A
N
N
Suponiendo una superficie cuadrada de lado a
Reluctancia del hierro
l−g
R =
h µaa
Reluctancia total
R=
Operando
R = 1 (l − g + µ r g )
µa2
Reluctancia del entrehierro
l−g
g
+
µaa µo (a + g )2
Ro =
g
µo (a + g )2
a +g ≈a
Para una permeabilidad relativa de 1000, cada milímetro de entrehierro supone un
aumento equivalente a 1 metro de hierro, así como lo correspondiente en la reluctancia
total.
CIRCUITOS MAGNÉTICOS
Nº 3
Las dimensiones del circuito de la
figura vienen dadas en centímetros. El
área transversal es de 25 cm2, la
permeabilidad
relativa
del
material
ferromagnético es 4000 y el número de
espiras de la bobina 400. Se quiere
calcular el valor de la corriente necesaria
en la bobina para que la inducción
magnética en el punto A tenga un valor de
B=0,5 Wb/m2, en cada uno de los
siguientes casos:
1.- Suponiendo que no hay pérdidas de flujo (reluctancia del aire infinita).
2.- Suponiendo que la dispersión se produce en la ventana del nícleo.
3.- Suponiendo que la dispersión solamente se produce alrededor de la columna
donde se encuentra la bobina.
Resolución Sin Considerar el Flujo de Dispersión
φ
Circuito magnético:
lh=2x25+2x15=0.8 m y Ah=25 cm2=0.0025 m2
l
0.8
ℜ = h =
= 2 105 Av ≈ 63662 Av
h µ A
−4 π
Wb
Wb
h h 4000 µ0 25 10
φ ℜ
1.2510−3 2105
π
i = A h=
= 0.1989A
0
N
400
Flujo de dispersión en la ventana del núcleo
φ
φ
φ
Reluctancia mitad núcleo magnético:
1
Av
Av
ℜ
ℜ h1 = h = 105
= 31831
π
2
Wb
Wb
Reluctancia de ventana: lh=10 cm=0.1 m y Ah=20x5 cm2=0.01 m2
No se toma un área mayor debido a que el flujo está muy conducido.
ℜa =
la
01
.
25 6 Av
Av
10
7957747
=
=
=
µ 0A a µ 0 10−2 π
Wb
Wb
Mediante Millmann:
Ni
1
ℜ
ℜa
1
h1 = Ni
=ℜ φ
ℑ
=
= Ni
AB
1 2ℜa + ℜ
1 ℜ
h1 A
2 + 1
h
1
h
1
2+
ℜ
ℜa
ℜa
h1
ℜ
φ ℜ
A
1
h
i =
(2 + h1 ) = 0.198943A
1
ℜa
N
El flujo de dispersión es el 0.4% de φA:
φ ℜ
ℑ
AB
= A h1 = 1 φ = 5 10−6 Wb
φ =
d ℜa
ℜa
250 A
Flujo de dispersión alrededor de la columna de la bobina
φ
φ
φ
Reluctancias del núcleo magnético
ℜ h2 =
3
ℜh
16
ℜ h3 =
5
ℜh
16
Área útil de flujo de dispersión: ≈ 3 ó 4 veces las dimensiones transversales. Eligiendo
4 veces: la=10cm=0.1m y Aa=(20x20-5x5)cm2=0.0375 m2
l
01
.
2 7 Av
ℜa = a =
=
10
µ 0A a µ 0 3.7510−2 3π
Wb
Millmann
Ni
2
ℜ
1
h2
ℑ
=
= Ni
= (ℜ + 2ℜ )φ
2
AB
h2
h3 A
ℜ
ℜ
1 +
1
1
+
h
2
h
2
+
+
1
ℜ
ℜa
ℜ + 2ℜ
ℜa
ℜ + 2ℜ
h2
h2
h3
h2
h3
ℜ
ℜ
φ ℜ
i = A h [1+ h 2 (1− h 2 )] = i (1+ 117 ) = 1.00457i = 0.19985 A
2
0
0
N
ℜa
ℜ
25600
h
Flujo de dispersión del 2,4% de φA
φ ( ℜ + 2ℜ h3 )
39
ℑ
φd = AB = A h2
=
φA ≈ 310−5 Wb
ℜa
ℜa
1600