Probabilidad y Estadística
Anuncio

Probabilidad
y
Estadística
Conteo con reemplazamiento
Considerando ahora un experimento en que una bola,
seleccionada de una caja con n bolas, se regresa a la
misma caja. Si se hace un total de k selecciones de esta
forma, el espacio muestral S contiene todos los
vectores de la forma:
A este proceso se le llama muestreo con
reemplazamiento.
Como existen n posibles resultados para cada una de
las bolas/selecciones, el número total de vectores en S
es
Conteo con reemplazamiento
Si en el experimento anterior quisieramos saber la
probabilidad del evento A en que cada una de las k
bolas seleccionadas sean distintas.
El número de vectores donde los k componentes son
distintos está dado por
Como el tamaño del espacio muestral es
la probabilidad del evento es
, entonces
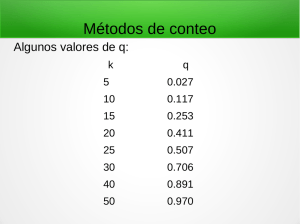
Métodos de conteo
Ejemplo:
El problema del cumpleaños (versión simplificada)
Un planeta gira alrededor del sol en 3 días. ¿Cuál es la
probabilidad de que Manolo y Juan cumplan años en
diferente fecha (sin considerar el año) en ese planeta?
Las posibilidades son:
Y la probabilidad de cada uno de estos resultados es:
Métodos de conteo
Problema del cumpleaños:
¿Cuál es la probabilidad de que al menos dos personas
de un grupo de k personas (2< k < 365) hayan nacido
el mismo día (festejen su cumpleaños).
Supongamos que los nacimientos son independientes
(gemelos son excluidos!). Entonces para cada una de
las k personas hay 365 posibilidades. Por tanto, el
espacio muestral es
Métodos de conteo
La probabilidad de que todos los cumpleaños sean
distintos es
Así pues, la probabilidad de que al menos dos personas
tengan el mismo día su cumpleaños es
Métodos de conteo
Combinaciones
Supongamos que tenemos un conjunto con n distintos
elementos (distinguibles), de los cuales escogemos k
elementos.
¿Cuál es el número de subconjuntos diferentes que se
pueden formar con los n elementos?
●
●
En este problema el orden de los elementos es
irrevelante
No hay dos combinaciones que tengan los mismo
elementos
Métodos de conteo (combinaciones)
Cada subconjunto se trata como una unidad y a ésta se
le llama combinación.
El número de combinaciones se denota por:
(n combinación k)
Ejemplo: un conjunto contiene los elementos a,b,c,d.
¿Cuál es el número de subconjuntos de 2 elementos
que podemos formar?
Respuesta:
{a,b},{a,c},{a,d},{b,c},{b,d},{c,d}
Métodos de conteo (combinaciones)
Ejemplo: Se quiere seleccionar un comité de 8
personas de un grupo de 20. ¿Cuál es el número de
comites que pueden formarse?
Respuesta: número de combinaciones de 8 elementos
tomados de un grupo de 20.
Métodos de conteo (combinaciones)
Teorema del binomio
Métodos de conteo (combinaciones)
Ejemplo:
Supongamos que lanzamos una moneda 10 veces y
queremos determinar
a) la probabilidad de obtener 3 caras exactamente
b) la probabilidad de obtener 3 caras, o menos
Métodos de conteo (combinaciones)
Ejemplo (usando regla de multiplicación):
En una clase hay 15 hombres y 30 mujeres. De estos 45
estudiantes, 10 serán seleccionados aleatoriamente. ¿Cuál es la
probabilidad de que 3 hombres sean seleccionados?
Métodos de conteo (combinaciones)
Ejemplo (playing cards):
Un paquete de 52 cartas se distribuyen entre 4 jugadores, de
modo que cada jugador recibe 13 cartas. Si el paquete contiene
4 aces, determinar la probabilidad de que cada jugador reciba
un as.
Coeficientes multinomiales
Generalización de los coeficientes binomiales.
Veamos antes un ejemplo:
Supongamos que con 20 personas se forman 3 comités:
A, B y C. Los comités A y B tendrán 8 miembros,
mientras que C tendrá 4 miembros.
¿Cuál es el número de formas posibles en que las 20
personas pueden repartirse en cada uno (y sólo uno) de
los comités?
Coeficiente multinomiales
Supongamos que tenemos n elementos distintos que
serán repartidos en k
grupos, de modo que
para
, el j-ésimo grupo contiene
exactamente
elementos, donde
Entonces, el número de formas distintas en que los n
elementos pueden repartirse entre los k grupos puede
obtenerse de la siguiente forma:
a) Los
elementos del primer grupo pueden
seleccionarse de los n elementos disponibles de
formas.
Coeficientes multinomiales
b) Los
elementos del segundo grupo pueden
seleccionarse de los restantes
elementos de
formas distintas.
De aquí que el número total de formas distintas de
seleccionar los dos primeros grupos es
c) Continuando con este procedimiento para el tercer
grupo tenemos
formas posibles de
escoger
elementos y un total de
formas para los 3 grupos
Coeficientes multinomiales
Por lo tanto, el número total de modos distintos de
seleccionar/repartir n elementos en k grupos es
Al número
coeficiente multinomial
se le llama
Coeficientes multinomiales
Ejemplo
En un paquete de cartas (52 cartas), 13 son corazones.
Suponga que las cartas serán repartidas entre 4
jugadores A, B, C y D. De modo que cada jugador
recibirá 13 cartas. ¿Cuál es la probabilidad de que el
jugador A reciba 6 corazones, el jugador B, 4
corazones; C, 2 corazones y el jugador D, un corazón?
Combinaciones (con reemplazamiento)
Así como hemos visto en el caso de las permutaciones,
ahora nos preguntamos por el número de
combinaciones de k elementos seleccionados de n con
reemplazamiento.
Antes veamos un ejemplo para ver que hay una
relación uno a uno entre el número de combinaciones
de tamaño k (de n objetos) con reemplazamiento y el
número de combinaciones de muestras de tamaño k (de
n+k-1 objetos), sin reemplazamiento.
Combinaciones (con reemplazamiento)
Consideremos 3 bolas con los números 1, 2 y 3:
es decir, n=3 y k=3
Combinaciones (con reemplazamiento)
1,1,1
1,1,2
1,1,3
1,2,2
1,2,3
1,3,3
2,2,2
2,2,3
2,3,3
3,3,3
Muestras con reemplazo
k=3, n=3
-------- 1,2,3
-------- 1,2,4
-------- 1,2,5
-------- 1,3,4
-------- 1,3,5
-------- 1,4,5
-------- 2,3,4
-------- 2,3,5
-------- 2,4,5
-------- 3,4,5
|
Muestras sin reemplazo
k=3, n+k-1=5
Combinaciones (con reemplazamiento)
Es decir, el número de combinaciones con
reemplazamiento de k objetos seleccionados de n
está dado por
Enfoque físico
Supongamos que tenemos k partículas
indistinguibles que queremos repartir en n niveles
(cajas) distinguibles
¿De cuántas formas distintas se pueden repartir las
partículas?
Estadística de Maxwell-Boltzmann, BoseEinstein y Fermi
Un sistema contiene un número de partículas N. La
estructura del sistema es tal que existen R niveles de
energía, con energías
y cada
nivel de energía contiene
(degeneración) estados
cuánticos.
Encuentre el número de formas posibles en que las
partículas se pueden repartir entre los estados
cuánticos, tal que el i-ésimo nivel de energía contenga
partículas, bajo las siguientes condiciones:
Estadística de Maxwell-Boltzmann, BoseEinstein y Fermi
a) Las partículas son distinguibles y no hay restricción
alguna en el número de partículas en cada estado.
b) Las partículas son indistinguibles y no hay
restricciones en cuanto al número de partículas en cada
estado.
c) Las partículas son indistinguibles con un máximo de
una partícula en cada estado.
Estadística de Maxwell-Boltzmann, BoseEinstein y Fermi
Estadística de Maxwell-Boltzmann, BoseEinstein y Fermi
Olvidémonos por un momento de la degeneración en
cada nivel.
●
Caso a: Si las partículas son distinguibles entonces
ya sabemos el resultado: recién hemos visto el
número de formas distintas en que n objetos pueden
repartirse en k grupos (en nuestro caso k=R). De
aquí que
es el número de arreglos distintos que podemos
hacer con las N partículas
Estadística de Maxwell-Boltzmann, BoseEinstein y Fermi
●
Caso b:
Ahora, si las N partículas son indistinguibles de
cuántas formas distintas se pueden repartir éstas en los
R niveles, con
partículas en cada nivel :
De una sóla forma !
Estadística de Maxwell-Boltzmann, BoseEinstein y Fermi
Ahora vamos a considerar la degeneración.
Llamemos
al número de formas en que las
partículas pueden distribuirse/acomodarse en el iésimo nivel de energía
.
De esta forma el número de posibles formas distintas
en que las N partículas pueden repartirse en los R
niveles con
partículas por nivel es:
Partículas distinguibles
Partículas indistinguibles
Estadística de Maxwell-Boltzmann, BoseEinstein y Fermi
Nos resta tener una expresión para
Caso a:
Como no hay restricción en el número de partículas en
cada estado, cada partícula en el i-ésimo nivel puede
estar en cualquiera de los
estados, i.e.,
Estadística de Maxwell-Boltzmann, BoseEinstein y Fermi
Por lo tanto, para el caso a, tenemos finalmente que
Esta es la llamada estadística de Maxwell-Boltzmann
que se utiliza en mecánica estadística clásica.
Estadística de Maxwell-Boltzmann, BoseEinstein y Fermi
Caso b:
Ahora las partículas son indistinguibles y no hay
restricción en el número de partículas en cada estado.
Por tanto:
Estadística de Bose-Einstein