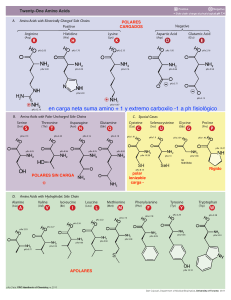
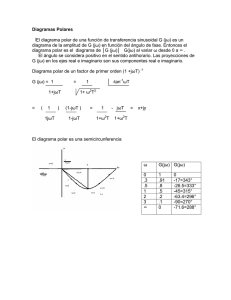
diagramas polares
Anuncio

DIAGRAMAS POLARES Diagrama Polar de G(jω): Diagrama de la amplitud de G(jω) en función del ángulo de fase de G(jω) en coordenadas polares al variar ω desde cero a infinito. X(s) G1(s) Y(s) Z(s) G2(s) Z(s) = G1 ( jω) G 2 ( jω) = G (s) X(s) G ( jω) = G1 ( jω) G 2 ( jω) G ( jω) = G1 ( jω) G 2 ( jω) ∠G ( jω) = ∠G1 ( jω) + ∠G 2 ( jω) Im |G2(jω)| <G2 |G1(jω)| |G1(jω)G2(jω)| <G1 <G1+<G2 Re DIBUJO DE LOS DIAGRAMAS POLARES a) Factores integral y derivativo (jω)± 1 G ( jω) = 1 1 1 = − j = ∠ − 90° jω ω ω eje imaginario negativo G(jω) = jω = ω ∠90° eje imaginario positivo Im Im a) ω=∝ b) ω=0 Real Real ω=∝ ω=0 b) Factores de primer orden (1+jωT) ± 1 Im G ( jω) = Para 1 1 = ∠ − tan −1 ωT 2 2 1 + jω T 1+ ω T ω=0 ω = 1/T ω=∝ ω=0 ω=∝ 0.5 Real G(j0) = 1∠0° 1 G(j/T) = ∠-45° 2 G(j∝) = 0∠-90° G(j1/T) 2 -1 ω=0 G(j0) = 1∠0° ω = 1/T G(j/T) = 2 ∠+45° ω=∝ G(j∝) = ∝∠90° c) Factores cuadráticos [1+2ξ(jω/ωn)+(jω/ωn)2] ± 1 ω=∝ Im G(jω) = 1+jωT = 1 + ω T ∠tan ωT 2 1 G(j1/T) Para ω=0 0 1 Real G ( jω) = 1 [] = 1 2 ⎛ ⎜1 − ω ⎜ ω 2 ⎝ n ⎞ ⎛ ⎟ + ⎜ 2ξ ω ⎟ ⎜⎝ ω n ⎠ ⎞ ⎟⎟ ⎠ 2 ∠ − tan −1 2ξω / ω n (1 − ω 2 ω n 2 ) Im Para ω=0 ω = ωn ω=∝ G(j0) = 1∠0° 1 ∠-90° G(j/T) = 2ξ G(j∝) = 0∠-180° 0.5 ω ω=∝ ωn ⎞ ⎟⎟ ⎠ 2 lim G ( jω) = 1 ∠0° ω→0 ω→∞ lim G ( jω) = ∞ ∠180° ω→∞ ξ >0 ωn ξpeq ω →∝ Im ω=0 0 ω→0 Real ξgde ωn El punto del diagrama polar cuya distancia al origen es máximo corresponde a la frecuencia de resonancia ωr . ⎛ ω ⎞ ⎛ ω ⎟⎟ + ⎜⎜ j G ( jω) = 1 + 2ξ⎜⎜ j ω ⎝ n ⎠ ⎝ ωn ⎛ ω 2 ⎞⎟ ⎛ 2ξω ⎞ ⎜ ⎟ = 1− + j⎜ ⎜ ω 2 ⎟ ⎜⎝ ω n ⎟⎠ ⎝ n ⎠ = 01 1 Real FORMAS GENERALES DE LOS DIAGRAMAS POLARES G ( jω) = K (1 + jωT1 ) (1 + jωT2 )..........(1 + jωTp ) ( jω) n (1 + jωTa ) (1 + jωTb )..........(1 + jωTq ) Grado del denominador > grado del numerador (q > p) n = 0 Sistema tipo cero G ( jω) = G ( jω) = K (1 + jωT1 ) (1 + jωT2 )..........(1 + jωTp ) (1 + jωTa ) (1 + jωTb )..........(1 + jωTq ) K 1 + ω 2 T12 1 + ω 2 T2 2 ..... 1 + ω 2 Ta 2 1 + ω 2 Tb 2 ..... ∠G ( jω) = tan −1 ωT1 + tan −1 ωT2 + .... − tan −1 ωTa − tan −1 ωTb − .... Para ω=0 ω=∝ G(j0) = K∠0° G(j∝) = 0∠ El diagrama siempre empieza en el eje real positivo (en el valor de K, que es también el coeficiente estático de error de posición Kp). n = 1 Sistema tipo 1 K (1 + jωT1 ) (1 + jωT2 )..........(1 + jωTp ) G ( jω) = jω ⋅ (1 + jωTa ) (1 + jωTb )..........(1 + jωTq ) G ( jω) = K 1 + ω 2 T12 1 + ω 2 T2 2 ..... ω 1 + ω 2 Ta 2 1 + ω 2 Tb 2 ..... ∠G ( jω) = tan −1 ωT1 + tan −1 ωT2 + .... − 90° − tan −1 ωTa − tan −1 ωTb − .... ω=0 ω=∝ Para G(j0) = ∝∠-90° G(j∝) = 0∠ n = 2 Sistema tipo 2 G ( jω) = K (1 + jωT1 ) (1 + jωT2 )..........(1 + jωTp ) ( jω) 2 (1 + jωTa ) (1 + jωTb )..........(1 + jωTq ) G ( jω) = K 1 + ω 2 T12 1 + ω 2 T2 2 ..... ω 2 1 + ω 2 Ta 2 1 + ω 2 Tb 2 ..... ∠G ( jω) = tan −1 ωT1 + tan −1 ωT2 + .... − 180° − tan −1 ωTa − tan −1 ωTb − .... Para ω=0 ω=∝ G(j0) = ∝∠-180° G(j∝) = 0∠