Profr.(a)
Anuncio

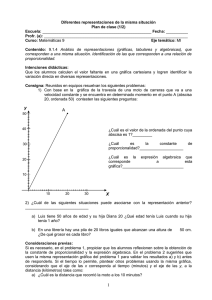
Plan de clase (1/3) Escuela:_____________________________________ Profr.(a): ___________________________________ Curso: Matemáticas 8 Fecha: _____________ Eje temático: MI Contenido 8.4.4: Análisis de las características de una gráfica que represente una relación de proporcionalidad en el plano cartesiano. Intenciones didácticas: Que los alumnos reflexionen en la ubicación de puntos en el plano cartesiano con base en las características del par ordenado. Consigna: Organizados en equipos realicen la siguiente actividad. A partir de la siguiente figura en el primer cuadrante del plano cartesiano, construyan la figura simétrica A’B’C’D’ con respecto al eje vertical. Posteriormente contesten lo que se pide. a) ¿Cuáles son las coordenadas de los puntos A, B, C y D?__________________ ordenada y 5 4 3 2 1 -5 -4 -3 -2 -1 -1 -2 -3 -4 -5 1 A . b) ¿Qué nombre recibe el primer componente de cada par ordenado? __________________________________ _________________________________ C D c) ¿Qué nombre recibe el segundo componente de cada par ordenado? __________________________________ 2 3 B 4 5 x abscisa d) ¿Cuáles son las coordenadas de los puntos A’, B’, C’ y D’? _______________________________ _______________________________ _______________________________ Consideraciones previas: Se recomienda inducir a los alumnos a la aplicación de los concpetos y terminología que corresponde al desarrollo del tema. Si el tiempo lo permite, conviene reforzar lo aprendido con los siguientes planteamientos: a) Si a la primera coordenada de cada vértice del cuadrado ABCD le sumamos dos unidades. ¿Qué transformación tendrá la figura? ___________________________________________________________________ ___________________________________________________________________ ¿Cuáles serían las nuevas coordenadas de los vértices?________________________ b) Si a la segunda coordenada de cada vértice del cuadrado ABCD le restamos cinco unidades. ¿Qué transformación tendrá la figura? ___________________________________________________________________ ___________________________________________________________________ ¿Cuáles serían las nuevas coordenadas de los vértices? _______________________ Observaciones posteriores: 1. ¿Cuáles fueron los aspectos más exitosos de la sesión? ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ______ 2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase? ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ______ 3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para usted. Muy útil Útil Uso limitado Pobre Plan de clase (2/3) Escuela:_____________________________________ Profr.(a): ____________________________________ Curso: Matemáticas 8 Fecha: _____________ Eje temático: MI Contenido 8.4.4: Análisis de las características de una gráfica que represente una relación de proporcionalidad en el plano cartesiano. Intenciones didácticas: Que los alumnos distingan la gráfica de una relación proporcional de una que no lo es, con base en la interpretación de sus características. Consigna: Organizados en equipos realicen la siguiente actividad: Observen las siguientes gráficas que representan relaciones entre dos variables y anoten en el cuadro las características que se piden. (realizar una cuadricula en cada gràfica para precisar los datos) Gráfica 1. Relación de litros de gasolina y su costo. Gráfica 2. Relación de los litros de agua que caen cada hora en un tinaco. Gráfica 3. Relación de la estatura de Pedro y su edad. Grafica Tipos de características 1 2 3 Tipo de línea Relación del valor de x con respecto a y Tipo de variación Considerando la información del cuadro: ¿Cuál gráfica representa una relación proporcional? Y, ¿Por qué? ________________________________________________________________________ Consideraciones previas: Si se les dificulta establecer la relación proporcional, debe inducirse a los alumnos a que reflexionen sobre un análisis comparativo de la relación: litros de gasolina y su costo, ¿es constante o variable?, o bien; ¿los aumentos de “y” respecto a “x” son constantes?; ¿por cada “x”, cuanto aumenta “y”? ¿Los puntos generados por las coordenadas están alineados o no? Lo mismo en el caso del agua del tinaco y de las edades. En la confrontación, si los equipos presentan gráficas con características incompletas, estas deberán complementarse con la participación de los demas equipos. Es de gran importancia que en la confrontación se le dé énfasis a las características que pueden distinguir una relación proporcional. Observaciones posteriores: 1. ¿Cuáles fueron los aspectos más exitosos de la sesión? ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ______ 2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase? ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ______ 3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para usted. Muy útil Útil Uso limitado Pobre Plan de clase (3/3) Escuela:_________________________________________ Profr.(a): ________________________________________ Curso: Matemáticas 8 Fecha: _____________ Eje temático: MI Contenido 8.4.4: Análisis de las características de una gráfica que represente una relación de proporcionalidad en el plano cartesiano. Intenciones didácticas: Que los alumnos a partir del análisis de la gráfica determinen la relación de proporcionalidad y su expresión algebraica; concluyendo con las características que debe tener toda relación proporcional. Distancia (km) Consigna: Organizados en equipos, analicen la siguiente gráfica, la cual representa la relación del tiempo y la distancia recorrida en una caminata que realizó Ernesto. Posteriormente contesten lo que se pide. 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 0 1 2 3 4 Tiempo (h) a) ¿A qué velocidad se desplazó Ernesto?_________________________________________ ____________________________________________________________________ _____ b) Si la velocidad de Ernesto hubiera sido mayor, ¿Qué cambio tendría la gráfica? Explique _____________________________________________________________________ _____________________________________________________________________ __________ c) ¿Podría cortar la recta al eje vertical por un punto diferente al origen? Si No ¿Por qué?___________________________________________________________________ __ _______________________________________________________________________ ______ d) Si la velocidad de Ernesto no hubiera sido constante, ¿Cómo se reflejaría este hecho en la gràfica?_______________________________________________________________ ___ ____________________________________________________________________ ______ Con los datos de la gráfica, registren en la siguiente tabla los valores que faltan: Tiempo (h) Distancia (km) 0.5 1 3 6 7.5 10.5 e) Si x es el tiempo y y la distancia recorrida, ¿qué expresión algebraica representa la caminata de Ernesto? Consideraciones previas: Si los alumnos tuvieran dificultad para relacionar la velocidad que alcanzó Ernesto en la caminata con la inclinación de la recta en la grafica, se les podría solicitar que representen en el mismo plano cartesiano la recta resultante aumentando la velocidad de 3km/h. Si se observan dificultades para tabular o trazar la gráfica del aumento de la velocidad de Ernesto, habría que reflexionar el significado de que la recta inicie en el punto (0,0) ya que Ernesto inicia la caminata teniendo 0 de velocidad (parado). Es importante que la interacción de los alumnos en torno a las actividades desarrolladas, se orienten a formalizar que las técnicas de representación de una relación funcional son tablas, gráficas y expresiones algebraicas, pero que cada una tiene diferente utilidad en el análisis de las características de las funciones. Esto es, que la situación problemática se puede resolver y explicar a través del llenado de tablas, de la determinación y uso de una expresión algebraica y de la construcción e interpretación de su gráfica; y que, la unicidad de estas formas de representación son importantes para el desarrollo del concepto de proporcionalidad. Si el tiempo lo permite, incluir en la consigna: De manera individual, planteen una situación de proporcionalidad directa y construyan la gráfica correspondiente. Observaciones posteriores: 1. ¿Cuáles fueron los aspectos más exitosos de la sesión? ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ______ 2. ¿Cuáles cambios considera que deben hacerse para mejorar el plan de clase? ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ______ 3. Por favor, califique el plan de clase con respecto a su claridad y facilidad de uso para usted. Muy útil Útil Uso limitado Pobre