Ejercicio sobre el PIB histórico anual español El gráfico adjunto
Anuncio
Ejercicio sobre el PIB histórico anual español1
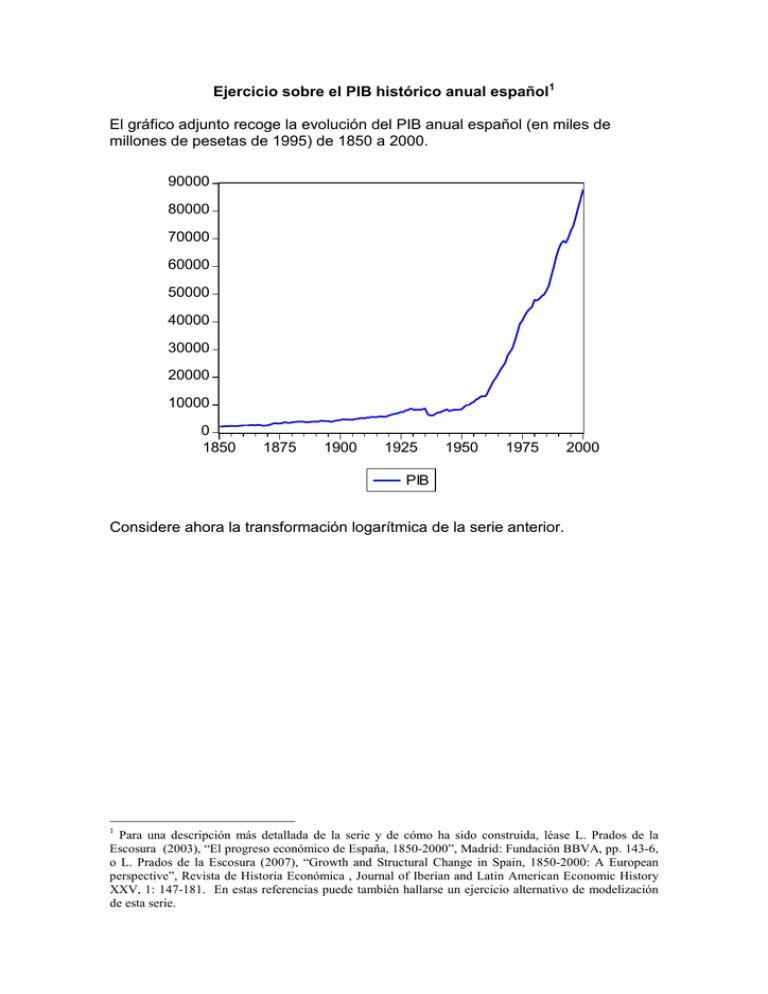
El gráfico adjunto recoge la evolución del PIB anual español (en miles de
millones de pesetas de 1995) de 1850 a 2000.
90000
80000
70000
60000
50000
40000
30000
20000
10000
0
1850
1875
1900
1925
1950
1975
2000
PIB
Considere ahora la transformación logarítmica de la serie anterior.
1
Para una descripción más detallada de la serie y de cómo ha sido construida, léase L. Prados de la
Escosura (2003), “El progreso económico de España, 1850-2000”, Madrid: Fundación BBVA, pp. 143-6,
o L. Prados de la Escosura (2007), “Growth and Structural Change in Spain, 1850-2000: A European
perspective”, Revista de Historia Económica , Journal of Iberian and Latin American Economic History
XXV, 1: 147-181. En estas referencias puede también hallarse un ejercicio alternativo de modelización
de esta serie.
12
11
10
9
8
7
1850
1875
1900
1925
1950
1975
2000
LPIB
A la transformación logarítmica del PIB se le ha ajustado el siguiente modelo:
LPIBt = α 0 + α 1t + u t
donde t es la tendencia.
Dependent Variable: LPIB
Method: Least Squares
Date: 07/01/08 Time: 12:39
Sample: 1850 2000
Included observations: 151
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
Tendencia
7.309707
0.023356
0.053870
0.000615
135.6908
37.98540
0.0000
0.0000
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.906401
0.905772
0.329342
16.16148
-45.54371
0.019935
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob(F-statistic)
9.084764
1.072898
0.629718
0.669682
1442.891
0.000000
12
11
10
9
.8
8
.4
7
.0
-.4
-.8
1850
1875
1900
Residual
1925
1950
Actual
1975
2000
Fitted
En cuanto a la especificación del comportamiento tendencial del modelo,
una de las hipótesis sobre los errores es que ellos deben ser
estacionarios, ya que todo el comportamiento evolutivo tendencial y/o
estacional debe ser capturado por el modelo que proponemos.
Observando la grafica vemos que los residuos presentan oscilaciones de
nivel y consecuentemente no son estacionarios. Esto revela que el modelo
estimado aunque presente una R2 elevada y los parámetros sean
estadísticamente significativos no ajusta perfectamente a los datos.
Además vemos que los residuos presentan la existencia de rupturas en la
tendencia que deben ser introducidas en el modelo original.
La nueva propuesta de modelo debe captar el impacto de la guerra civil
sobre el PIB. De hecho, de la gráfica se observa un quiebre de nivel
acentuado del LPIB en 1936 que se prolonga hasta 1939. Para captar
esto suceso creamos una variable artificial D(36-39)t que se caracteriza
por:
1
D(36 _ 39)t
0
t = {1936, 1937, 1938, 1939}
t ≠ {1936, 1937, 1938, 1939}
Además de este quiebre en el nivel se puede observar otro que
corresponde al periodo de 1940 al 1954. Durante este periodo se
observa una ligera recuperación del nivel del LPIB en relación con el
periodo de la guerra civil, pero es suficiente para alcanzar el nivel previo
a la guerra. Por lo tanto, la variable artificial D(40-54)t se caracteriza por:
1
D( 40 _ 54 )t =
0
t = {1940, 1941,..., 1954}
t ≠ {1940, 1941, ..., 1954}
Nótese que estas variables ficticias sólo modifican el nivel de la serie en
estos periodos, pero suponen que la tasa de crecimiento se mantiene
constante. Sin embargo, desde 1960 pueden observarse dos rupturas en
este crecimiento. Una que abarca 1960 a 1974, con un ritmo de
crecimiento mayor que el que venía dándose los años anteriores, y luego
en 1974, vuelve a bajar la tasa, producto quizá a la crisis del petróleo.
Para eso se crean otras dos variables artificiales que se caracterizan por:
t ≤ 1960
0
D36t
y
t - 111 t > 1960
t ≤ 1974
0
D74t
t - 125 t > 1974
Así, el posible modelo determinista con tendencias segmentadas y
cambios de nivel vendría dado por:
LPIBt = α 0 + α 1t + α 2 D36 _ 39t + α 3 D40 _ 56t + α 4 D60t + α 5 D74t + a t
MODELO CON DOS ESCALONES (36-39 Y 40-56) Y DOS QUIEBRES DE TENDENCIA (60 Y 74)
12
11
10
9
.2
8
.1
7
.0
-.1
-.2
1850
1875
1900
Residual
Dependent Variable: LPIB
Method: Least Squares
1925
1950
Actual
1975
Fitted
2000
Date: 04/16/08 Time: 12:40
Sample: 1850 2000
Included observations: 151
Y(t) = C + B(1) * t + B(2)* D60(t) + B(3)*D74(t) + A(1)*D36_39(t) + A(2)*D40_56(t) + U(t)
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
Tendencia
D60
D74
D36_39
D40_56
7.630055
0.016544
0.063818
-0.051266
-0.328366
-0.189172
0.012508
0.000218
0.002008
0.002936
0.033487
0.019941
609.9900
76.03922
31.78060
-17.46245
-9.805882
-9.486381
0.0000
0.0000
0.0000
0.0000
0.0000
0.0000
R-squared
Adjusted R-squared
S.E. of regression
Sum squared resid
Log likelihood
Durbin-Watson stat
0.996626
0.996509
0.063390
0.582645
205.3283
0.400376
Mean dependent var
S.D. dependent var
Akaike info criterion
Schwarz criterion
F-statistic
Prob(F-statistic)
9.084764
1.072898
-2.640111
-2.520219
8565.141
0.000000
Según los resultados de la estimación podemos decir que:
•
El crecimiento anual estimado del PIB hasta 1960 era aproximadamente
de 1.7%
•
Entre los años 1960 y 1973 la tasa de crecimiento anual estimada pasó
a ser del 8%.
•
A partir de 1974 se registró un crecimiento más lento del PIB, cerca del
2.9% anual.
•
En los años de la Guerra Civil el nivel del PIB cayó abruptamente (un
33%) relativamente al inicial (pasó de aproximadamente 2059 (miles de
millones de pesetas a precios de 1995) a 1483 (miles de millones de
pesetas a precios de 1995).
•
Luego de la Guerra Civil, el PIB se recuperó un poco en los años de
1940 a 1956, cuyo nivel sólo es menor en un 19% respecto a antes de la
guerra. En términos nominales, esto es aproximadamente 1704 miles de
millones de pesetas a precios del 1995 (relativamente al año base).











