Ab-initio
Anuncio
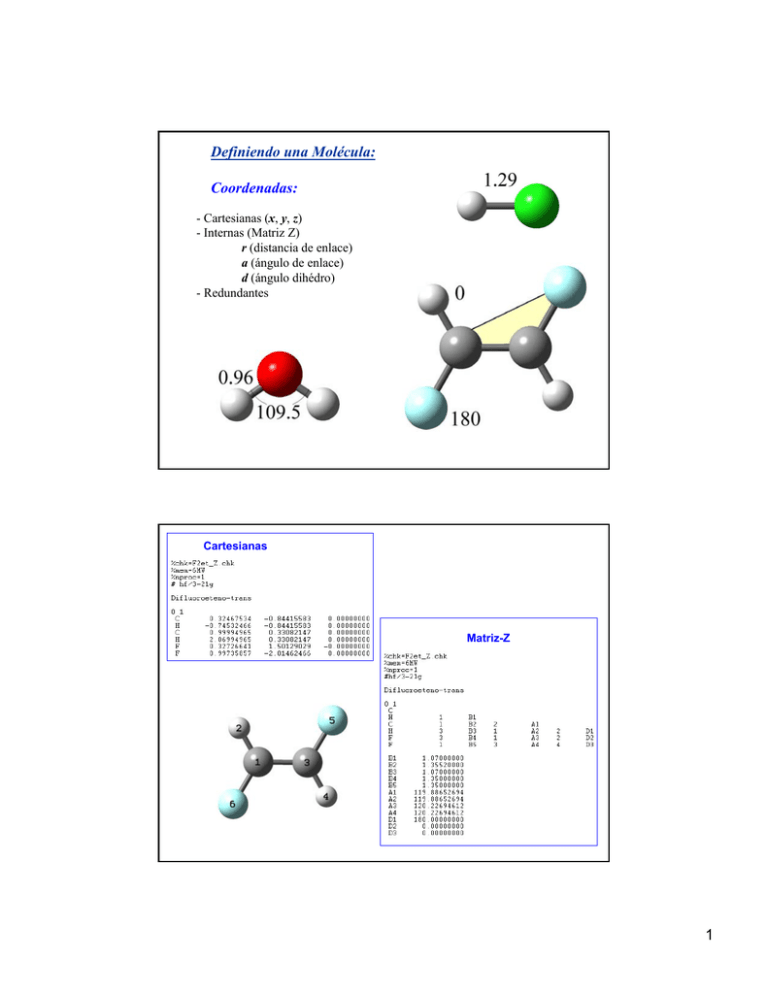
Definiendo una Molécula:
Coordenadas:
- Cartesianas (x, y, z)
- Internas (Matriz Z)
r (distancia de enlace)
a (ángulo de enlace)
d (ángulo dihédro)
- Redundantes
Cartesianas
Matriz-Z
1
Métodos más Comunes en Química Computacional:
-Ab-initio
-Semiempíricos
-Funcionales de la densidad (DFT)
-Mecánica Molecular
-Dinámica Molecular y Simulaciones Montecarlo
Ab-initio
-Pueden mejorarse sistemáticamente para aumentar su exactitud
-No es necesario parametrizar o calibrar con respecto al experimento
-Permite describir geometrias, propiedades, energética y reactividad
-Computacionalmente costosos
-Tratamiento estricto de la distribución electrónica por medio de la ecuación de Scrödinger:
lΨ = E Ψ
H
l=−
H
Partículas
∑
i
l =+
H
electrones
∑
i
∇i2 Partículas qi q j
+ ∑ ∑
rij
2mi
i< j
∇i2 =
∂2
∂2
∂2
+
+
∂xi2 ∂yi2 ∂zi2
∇i2 núcleos electrones Z i electrones
1
− ∑ ∑
+ ∑ ∑
rij
rij
2
i
j
i< j
2
Tiene en cuenta el efecto promedio de
la repulsión electrónica, pero no las
interacciones e- - e-
Ab-initio
Hartree-Fock (HF):
-Central Field aproximation
1
∑r
ij
-MO-LCAO
n
Ψ = ∑ ck χ k = c1 χ1 + c2 χ 2 + c3 χ 3 + .... + cn χ n
k
→
Iterativamente
Self-Consistent-Field (SCF)
{ci }inicial
E,
E,
{ci }
{ci }mejor
Convergencia
finales
HF: la probabilidad de encontrar a un electrón en una posición
determinada, depende de su distancia al núcleo pero no de la
distancia entre él y los otros electrones
Probabilidades idénticas
3
Møller-Plesset Perturbation Theory (MPn)
Incluye la correlación electrónica como una perturbación a la función de onda HF
H = H ( ) + λ H´
0
Ψ = Ψ + λ Ψ ( ) + λ 2 Ψ ( ) + λ 3 Ψ ( ) + λ 4 Ψ ( ) + .....
1
2
3
4
E = E + λ E ( ) + λ 2 E ( ) + λ 3 E ( ) + λ 4 E ( ) + .....
1
2
MP2
3
MP3
4
MP4
-Es el método más económico de introducir la correlación electrónica
-Buenos resultados para propiedades moleculares
-Converge en la mayoría de los casos
-Corrige de 80-90 % de la correlación electrónica para capa cerrada
-No debe usarse con bases pequeñas (< 6-31G*)
-Funciona bien para geometrías cercanas a la de equilibrio
-No se aplica a estados exitados
-Los cálculos de capa abierta pueden presentar errores de contaminación de spin
-No es variacional
Interacción de Configuraciones (CI):
HF
s im p le
N electrones,
s i m p le
d o b le
d o b le
M funciones de base
t r ip le
c u á d r u p le
(M>N)
Cada uno de los posibles arreglos de los N electrones en los M orbitales
recibe el nombre de configuración electrónica.
4
Interacción de Configuraciones (CI):
rs
Ψ = c0 Ψ 0 + ∑ car Ψ ra + ∑ cab
Ψ rsab +
a <b
r<s
r ,a
Estado
Base
a <b < c
r < s <t
rst
abc
Dobles
Excitaciones
Simples
Full CI
∑c
Ψ rst
abc + .......
Triples
Computacionalmente
Imposible
Solución:
Truncamiento
rs
Ψ CISD = c0 Ψ 0 + ∑ car Ψ ar + ∑ cab
Ψ rsab
a <b
r<s
r ,a
Geometrías muy buenas incluso con bases pequeñas
Propiedades como PI, momento dipolo, etc. con buena exactitud
~ el 93 % de la E correlación
No es consistente con el tamaño
MCSCF: Multi-Configuration Self Consistent Field
Los métodos configuracionales pueden considerarse como métodos CI donde no
sólo los coeficientes de la combinación lineal de determinantes de Slater se
optimizan por el principio variacional, sino que en cada ciclo se optimizan los
coeficientes de los orbitales moleculares individuales (en lugar de dejarlos fijos a
sus valores HF como en una CI).
rs
Ψ = c0 Ψ 0 + ∑ car Ψ ra + ∑ cab
Ψ rsab +
r ,a
a <b
r <s
∑c
a <b < c
r < s <t
rst
abc
Ψ rst
abc + .......
n
Ψ 0 = ∑ ck χ k = c1 χ1 + c2 χ 2 + c3 χ 3 + .... + cn χ n
k
5
MCSCF: Multi-Configuration Self Consistent Field
CASSCF: Complete Active Space SCF
Se dividen los OM en subconjuntos dependiendo de cómo van a ser usados
para construir la función de onda en:
1. Orbitales activos
2. Orbitales inactivos y
3. Orbitlaes externos
(secundarios o virtuales)
CAS
todas las
excitaciones posibles
(1) + (2) orbitales ocupados
(3) Orbitales vacios o virtuales
(2) Se mantienen doblemente
ocupados en todas las
configuraciones
Del espacio
activo
CC: Pares acoplados (Coupled Clusters)
Aproximación de pares electrónicos independientes (IEPA)
Calcula le energía de correlación de cada par, independientemente del resto
Reduce el problema de N e- a N(N-1)/2 problemas bielectrónicos
rs
Ψ IEPA = Ψ 0 + ∑ cab
Ψ rsab
r <s
IEPA :
-Equivalente a DCI para cada par independiente
-No puede llegarse a la E correlación exacta
ya que no se tiene en cuenta el acoplamiento entre los pares
CC: Introduce el acoplamiento entre pares
6
CC: Pares acoplados (Coupled Clusters)
rstu
rs
cabcd
≅ cab
∗ ccdtu
a→r
b→s
c→t
d →u
a→r
b→t
c→s
d →u
" abcd " → " rstu "
" abcd " → " rtsu "
" rstu " = − " rtsu "
rstu
rs
rs
rs
cabcd
≅ cab
∗ ccdtu = cab
∗ ccdtu − cab
∗ ccdtu
rs tu
tu
rs tu
rt su
rt su
= cab
+ cad
ccd − cacrs cbd
cbc − cab
ccd + cacrt cbdsu − cad
cbc
ru st
ru st
tu rs
tu rs
tu rs
+ cab
ccd − cacru cbdst + cad
cbc + cab
ccd − cac
cbd + cad
cbc
su rt
rt
su rt
st ru
st ru
− cab
− cad
ccd + cacsu cbd
cbc + cab
ccd − cacst cbdru + cad
cbc
rs
rs
Ψ CC = Ψ 0 + ∑ cab
Ψ ab
+
r <s
∑
a <b < c < d
r < s <t <u
rs
rstu
cab
∗ ccdtu Ψ abcd
+ ......
•consistente con el tamaño
• recupera mucha energía de correlación (comparando vs. MP2)
• muy costoso (mucho más que MP2).
7
Métodos Ab-initio:
Exactitud relativa:
HF MP 2 < CISD ≅ MP 4 ≅ CCSD < CCSD(T ) < Full CI
Fuentes de error:
1. La aproximación de Born-Oppenheimer
2. El uso de conjuntos de base incompletos
3. Correlación electrónica incompleta
4. No inclusión de efectos relativistas
Desventaja: Computacionalmente caros
Ventaja: Para moléculas muy pequeñas (<15 e-) resultados muy exactos
Para muchas moléculas de interés real, resultados de exactitud
comparable al experimento
8