,a a a a 3 R a a = + R a a = + R R
Anuncio

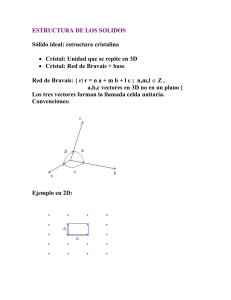
Ø Verificar si la siguiente red es una red Bravais (bidimensional, 2D): 1/41 Laboratorio de Simulación de Materiales no Metálicos Los puntos A y B no satisfacen la primera definición (un un conjunto infinito enumerable de puntos que tiene exactamente el mismo aspecto cuando se observa desde cualquiera de ellos ). Luego no es una red de Bravais (para demostrar que no es una red de Bravais, basta con un único contraejemplo) R2 A B a2 a1 R1 a1 , a2 generan puntos que pertenecen a la red, por ejemplo el vector R1 = 3a1 + a2 pero también puntos que no pertenecen a la red, como el R = a + a ; luego tampoco satisfacen la 2ª 2 1 2 De otra manera: los vectores primitivos definición Laboratorio de Simulación de Materiales no Metálicos 2/41 1 Ø La red hexagonal no es una red de Bravais Bravais,, sin embargo sí es una estructura cristalina (red + base). Muestra cómo puede construirse construirse la red hexagonal como una red de Bravais + una base. base malla El hexágono no es la celda unitaria del sistema hexagonal, ni en dos ni en tres dimensiones. En 2D es un rombo de ángulo agudo 60º. En 3D es un prisma recto construido sobre este rombo. Laboratorio de Simulación de Materiales no Metálicos 3/41 2