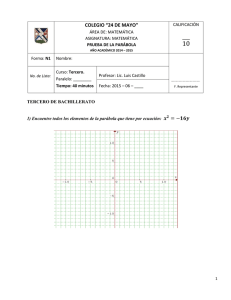
1. Hallar la ecuación de la circunferencia cuyo centro esta
Anuncio

UN I V E R S I D A D MA Y O R F A C U L T A D D E IN G E N I E R Í A PR I M E R SE M E S T R E 2011 GUÍA DE GEOMETRÍA ANALÍTICA 1. Hallar la ecuación de la circunferencia cuyo centro esta determinado por la intersección de las rectas x 4y = 1 y 2x y = 2 y su radio es 9. 2. Determine la ecuación de la circunferencia que pasa por los puntos(2; 2); ( 1; 4) y (4; 6) . p 3. Hallar la ecuación de la circunferencia de radio 5 2 2 y que pasa por la intersección de las circunferencias x2 +y 2 +2x 6y 16 = 0 y x2 +y 2 6x+2y = 0: 4. Hallar el centro y el radio de la circunferencia dada a) b) c) d) 2 2 (x 1) + (y 3) = 49 x2 + y 2 + 8y = 0 x2 + y 2 18x 6y 10 = 0 8x2 + 8y 2 + 16x + 64y 40 = 0 5. Considere la ecuación de la circunferencia x2 +y 2 = 8x+6y: Determine la ecuacion de la recta que es tangente a la circunferencia y que pasa por (11; 4) 6. Encuentre la ecuación de la recta que es tangente a la circunferencia de ecuación x2 2x = 2y y 2 en el punto (2; 2) : 7. Encuentre la ecuación de la parábola, la directriz, el foco si esta tiene como vértice (0; 0), pasa por el punto (4; 3) y el eje focal está en el eje X. 8. Encuentre la ecuación de la parábola, la directriz, su foco si esta tiene como vértice (6; 2), pasa por el punto ( 3; 5) y el eje focal es paralelo al eje X: 9. Encuentre la ecuación de la parábola, la directriz, su foco si esta tiene como vértice (0; 0), pasa por el punto (4; 3) y el eje focal est´a en el eje Y . 10. Encuentre la ecuación de la parábola, la directriz y su foco si esta tiene como vértice (6; 2) y pasa por el punto ( 3; 5) si su eje focal es paralelo al eje Y: 11. Encuentre la ecuación de la parábola de vertice V = (2; 3), foco en la recta 7x + 3y 4 = 0 y eje focal horizontal. 1 12. Considere la ecuación de la parábola 2x2 +5x+y 13 = 0. Encuentre toda la información posible a travez de su ecuación. 13. ciones. Gra…que y encuentre vértice , foco y directriz en las siguientes ecua- a) y 2 8x 4y + 4 = 0 b) y 2 + 8x 4y 28 = 0 c) y 2 + 1 = x d) y 2 x 6y + 11 = 0 e) y 2 6x + 6y + 27 + 27 = 0 f ) x2 = 4x 3y 7 g) 4y 2 48x 20y = 71 14. Indique que representa la ecuación x2 + 4x y encuentre todas sus componentes. 8y + 36 = 0, gra…quela 15. Determinar la ecuación de la parábola cuya directriz pasa por ( 3; 0) con vértice en el origen. 16. Determine la ecuación de la recta que es tangente a la parábola x2 = 5y en el punto (5; 5): 17. Gra…que y encuentre todos los elementos de la elipse de la ecuación. a) 9x2 + 2y 2 + 36x + 4y + 20 = 0 b) 16x2 + 9y 2 64x + 54y + 1 = 0 c) 25x2 + 16y 2 + 150x 64y = 102 d) 4x2 + 6y 2 = 12 e) x2 + 4y 2 6x + 16y + 21 = 0 18. Obtener la ecuación de la elipse cuyos focos son ( 1; 0) y (1; 0) y su diámetro mayor es 6. 19. Hallar la ecuación de la elipse de centro (1; 2), uno de los focos es (6; 2) y que pasa por el punto (4; 6) : 20. Determinar las coordenadas de los focos de la elipse 2x2 + 7y 2 = 3 21. El centro de una elipse esta en el punto (2; 4) el vértice y foco de un mismo lado del centro están en los puntos ( 2; 4) y ( 1; 4) respectivamente. Hallar la ecuación de la elipse. Complementar estos ejercicios con la bibliografía entregada en clases. 0 JU A N MU Ñ O Z HU R T A D O 2