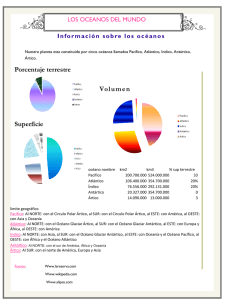
Incremento de esfuerzos producido por un terraplén

XXVI Reunión Nacional de Mecánica de Suelos
e Ingeniería Geotécnica
Sociedad Mexicana de
Ingeniería Geotécnica, A.C.
Noviembre 14 a 16, 2012 – Cancún, Quintana Roo
Incremento de esfuerzos producido por un terraplén
Stress increment produced by an embankment load
Miguel MANICA1
1
Estudiante de posgrado, Universidad Nacional Autónoma de México.
RESUMEN: La determinación del incremento de esfuerzo vertical en una masa de suelo debido a cargas superficiales es
una labor fundamental en el cálculo de asentamientos. En el caso de cargas producidas por la construcción de un
terraplén, las soluciones disponibles consideran únicamente una porción del mismo, y es necesaria la adecuada adición o
sustracción de dichas porciones para tomar en cuenta el efecto del terraplén completo. El presente artículo describe la
obtención de las expresiones fácilmente programables que permiten la determinación del incremento de esfuerzos
(vertical, horizontal y cortante) producido por un terraplén completo, en cualquier punto del medio. Se presenta un
ejemplo para ilustrar la aplicación de las expresiones obtenidas, así como los resultados de un programa de computadora
generado a partir de estas expresiones.
ABSTRACT: The vertical stress increment computation within a soil mass due to surface loads is a fundamental task for
settlements calculations. In the case of embankment loads, the available solutions only consider a portion of the
embankment and a suitable addition or subtraction of such portions is needed to take account the effect of the whole
structure. This paper describes the obtainment of the easily programmable equations allowing the stress increment
computation (vertical, horizontal and shear) due to the whole embankment, at any point of the half-space. An example is
presented to illustrate the use of the equations as well as the results of a computer program built from such equations.
1 INTRODUCCIÓN
1.1 Antecedentes
Debido a las condiciones de los proyectos para el
desarrollo de infraestructura, la construcción de
terraplenes sobre suelos blandos es cada vez más
común. En este tipo de suelo, generalmente los
estados límite de servicio rigen el diseño debido a su
gran compresibilidad, por lo que la estimación de los
asentamientos es una tarea fundamental en la
proyección de estas estructuras. No es suficiente
calcular los asentamientos en puntos característicos
como en el centro y en las orillas del terraplén; es
necesario determinarlos a lo largo de toda su
sección trasversal a fin de poder evaluar su
comportamiento y estar en condiciones de tomar
decisiones respecto a procedimientos constructivos
o viabilidad de los proyectos.
En el cálculo de asentamientos, es necesaria la
determinación del incremento de esfuerzos
verticales en la masa de suelo. Diversos autores han
recopilado soluciones obtenidas a partir de la teoría
de la elasticidad, tales como Jürgenson (1934), Gray
(1936), Newmark (1940), Poulos y Davis (1974). En
el caso de terraplenes, una de estas soluciones es
la obtenida por Carothers, la cual considera una
porción del terraplén limitada en uno de sus
extremos por un plano vertical. Analizando un punto
al centro del terraplén, basta con considerar una
porción que represente la mitad del mismo, y
multiplicar el esfuerzo obtenido por dos para tomar
en cuenta el efecto del terraplén completo. Para
puntos diferentes del centro, o incluso fuera del
terraplén, Osterberg (1957) utiliza el principio de
superposición, y mediante la correcta adición y
sustracción de estas porciones, obtiene el
incremento de esfuerzos verticales en cualquier
punto del medio. Además, para la determinación de
manera expedita del aporte de cada una de las
porciones, presenta una carta de influencia (Figura
1). El procedimiento de Osterberg, así como su carta
de influencia, han sido extensamente utilizados,
incluso en la literatura moderna (Tan, 2000; Jones et
al, 2008). Desafortunadamente, este procedimiento
tiene el inconveniente de volverse tardado y
laborioso si se requiere el análisis en numerosos
puntos.
1.2 Objetivos
El objetivo de este trabajo es el proporcionar las
expresiones
que
puedan
ser
fácilmente
implementadas en una hoja de cálculo, de tal forma
que, una vez introducidas las dimensiones del
terraplén y el peso específico del material que lo
conforma, únicamente sea necesario ir cambiando
SOCIEDAD MEXICANA DE INGENIERÍA GEOTÉCNICA A.C.
2
Distribución de esfuerzos producida por un terraplén sobre un medio elástico
las coordenadas del punto bajo análisis para obtener
el incremento de esfuerzos (vertical, horizontal y
cortante) producido por el terraplén completo en
dicha posición.
x 
p
x
z
2 z r1 
ln 
 2 x  b  
 
a
a
r0 
 
r2
 xz  
p  z z 2 



  a r22 
(2)
(3)
donde: p = γh; y γ = peso específico del material que
conforma el terraplén.
Figura 1. Carta de influencia para el cálculo de esfuerzos
verticales debido a una porción de terraplén (Osterberg,
1957).
1.3 Alcances
Se describe el desarrollo que permitió obtener las
expresiones antes mencionadas, se resuelve un
ejemplo para ilustrar la aplicación de éstas, y se
presentan los resultados de un programa de
computadora desarrollado en el lenguaje de
programación FORTRAN, con el fin de demostrar la
versatilidad
de
las
soluciones
obtenidas.
Adicionalmente se proporciona un enlace para
descargar una hoja de cálculo en EXCEL, donde se
encuentran
implementadas
las
ecuaciones
presentadas.
Figura 2. Solución de Carothers para la distribución de
esfuerzos producida por una porción de terraplén.
Es necesario poner los argumentos angulares β y α
en función de las coordenadas del punto bajo
análisis y de la geometría del terraplén. Se
considera el triángulo que forman los puntos ADB de
la Figura 2, tal como se muestra en la Figura 3,
donde:
  tan 1
bx
z
(4)
  tan 1
x a
z
(5)
2 DETERMINACIÓN DE LAS EXPRESIONES
Se parte de las ecuaciones obtenidas por Carothers
(Gray, 1936) para el cálculo del incremento de
esfuerzos (vertical, horizontal y cortante) en el caso
de deformación plana mostrado en la Figura 2, en
donde es analizada una porción de un terraplén
homogéneo,
sobre
un medio semi-infinito,
homogéneo, isótropo y linealmente elástico
(ecuaciones 1, 2 y 3).
z 

p
x
z
 2 x  b 
 
a
 
r2

(1)
SOCIEDAD MEXICANA DE INGENIERÍA GEOTÉCNICA A.C.
MANICA M.
Figura 3. Determinación del argumento angular β, y de las
distancias r1 y r2.
xB  2 b  x
3
(20)
Por lo tanto:
 '  90    90  tan 1
bx
z
(6)
 '  90    90  tan 1
x a
z
(7)
   '  '  180
  90  tan 1
  tan 1
(8)
bx
x a
 90  tan 1
 180
z
z
bx
x a
 tan 1
z
z
(9)
(10)
Se ponen también las distancias r2 y r1 en función de
las coordenadas del punto bajo análisis y de la
geometría del terraplén. Por conveniencia r2
permanece elevado al cuadrado.
r22  b  x 2  z 2

r1  x  a 2  z 2

(11)
1/ 2
(12)
De forma similar se determina α y r0 analizando el
triángulo formado por BDC de la Figura 2, con lo que
se obtiene:
  tan
1
ax
x
 tan 1
z
z

r0  x 2  z 2

1/ 2
(13)
(14)
Ahora todas las variables de las expresiones (1), (2)
y (3) están en función de la geometría del terraplén
(a, b, h), del peso específico del material que lo
conforma (γ) y de la posición del punto bajo análisis
(x, z), pero todavía se analiza únicamente una
porción del terraplén.
Considerando un terraplén con simetría, en la
Figura 4 se ensamblan dos sistemas (sistema A y B)
como el mostrado en la Figura 2.
Por simetría:
Figura 4. Ensamble de las dos porciones de un terraplén
De lo anterior, se obtienen los valores de β, α, r0 y r1
de ambos sistemas en función de las variables de
interés (ecuaciones 21 a la 28). En la Figura 4 puede
observarse que el valor de r2 es el mismo en ambos
sistemas, por lo que no se hace distinción de este
parámetro para cada uno de ellos (Ecuación 29).
Los argumentos angulares de las ecuaciones (21) a
la (24) se obtienen directamente en radianes.


bx
x a 
 tan 1

z
z  180
(21)


x b
2b  x  a  
 tan 1

z
z
 180
(22)


ax
x 
 tan 1 
z
z  180
(23)


a  2b  x
2b  x  
 tan 1

z
z  180
(24)
 A   tan 1
 B   tan 1
 A   tan 1
 B   tan 1

r0 A  x 2  z 2

1/ 2

(25)
r0 B  2 b  x 2  z 2



1/ 2
1/ 2
bA  bB  b
(15)
r1 A  x  a 2  z 2
aA  aB  a
(16)
hA  hB  h
r1B  2 b  x  a 2  z 2
(17)
z A  zB  z
(18)
Para tener ambos sistemas en función de las
mismas variables se considera lo siguiente:
xA  x
(19)

(26)
(27)

r22  b  x 2  z 2
1/ 2
(28)
(29)
Finalmente, basta con sumar el aporte de cada uno
de los sistemas a partir de las expresiones (1), (2) y
(3) tal como se hace en las ecuaciones (30), (31) y
(32), las cuales están referidas a la Figura 5.
SOCIEDAD MEXICANA DE INGENIERÍA GEOTÉCNICA A.C.
4
Distribución de esfuerzos producida por un terraplén sobre un medio elástico



x A
z
 2 x  b  
  A 

a
r2
 h 


z 


 


2 b  x  B
z
 2 b  x  
  B 
a
r2
 

(30)

x A
2 z r1 A  
z
ln
 2 x  b  
  A 
 
a
r0 A  
a
r2


 h 
2 b  x  B

x 
 (31)
  B 

 
a



 z
2 z r1B 
ln

 2 b  x  
a
r0 B 

 r2
 xz
 h z
2z2 

  A   B   2 
  a
r2 
(32)
Figura 6. Geometría del terraplén y ubicación del punto
bajo análisis.


1 9.15  12 .2
 tan

6
.
1
   0.519 rad
B  

 180


2
12
.
2
9
.
15
6
.
1


1
  tan

6 .1


A
6.1  9.15 


 tan 1
6.1
   0.519 rad

 180

1 9.15

  tan
6
.
1


B
6.1  2 12.2   9.15 


 tan 1
6 .1

   0.207 rad


 180
1 2 12 .2   9.15
 tan

6.10


r 22  12.2  9.15   6.10 2  46.513 m 2
2
Figura 5. Variables necesarias para el cálculo del
incremento de esfuerzos debajo de un terraplén.
Con las expresiones (21) a la (32) es posible
determinar las tres componentes de esfuerzo (σz, σx,
τxz) producidas por el terraplén completo,
únicamente en función de su geometría, el material
que lo conforma y la ubicación del punto bajo
análisis.
3 EJEMPLO
A partir del terraplén mostrado en la Figura 6, se
determina la magnitud del incremento de esfuerzo
vertical (σz) en el punto A.
Se calculan los valores de βA, βB, αA, αB y r22 con las
expresiones (21), (22), (23), (24) y (29)
respectivamente.

1 12.2  9.15 
 tan

6 .1
   0.927 rad
A  

1 9.15  6.1  180
  tan

6.1


Finalmente dichos valores son sustituidos en la
expresión (30) para determinar el incremento de
esfuerzo vertical:


9.15 0.519  
0.927 


6
.
1



6 .1




9.15  12.2 

18 5   46.513

z 


  
2 12.2   9.15 0.207  

0
.
519

 
6 .1

 

  6.1 12.2  9.15 
 
  46.513
 z  78.6 kPa
4 PROGRAMACIÓN DE LAS EXPRESIONES
Con el fin de mostrar la versatilidad de las
expresiones obtenidas, se generó una aplicación en
el lenguaje de programación FORTRAN, la cual
SOCIEDAD MEXICANA DE INGENIERÍA GEOTÉCNICA A.C.
MANICA M.
permite la determinación del incremento de esfuerzo
vertical en múltiples puntos simultáneamente.
Se tomó el ejemplo presentado en la Figura 6 y se
consideró como origen del sistema coordenado el
extremo izquierdo del terraplén (tal como debe de
hacerse al utilizar las expresiones deducidas en la
sección 2). Se determinó el incremento de esfuerzo
vertical desde x = -20.0 hasta x = 45.0 y desde z =
0.0 hasta z = 40.0 metros con separaciones en
ambas direcciones de un metro. Así, el programa
determinó el incremento de esfuerzo vertical en un
poco más de 2,700 puntos. Los resultados fueron
procesados con un software para construir mapas
de contornos. La Figura 7 muestra los resultados
obtenidos. En dicha figura también aparece indicada
la ubicación del punto que fue analizado en el
ejemplo de la sección 3, donde puede observarse
que en ambos cálculos el resultado obtenido es el
mismo.
Las ecuaciones obtenidas en el presente artículo,
también fueron implementadas en una hoja de
cálculo de EXCEL, la cual puede descargarse en el
siguiente enlace:
http://miguelmanica.webs.com/descargas
Figura 7. Mapa de contorno de la distribución del
incremento de esfuerzos verticales debajo de un terraplén.
5
no puede tomar valores negativos, sin embargo, el
valor de “x” sí puede hacerlo para tomar en cuenta
los puntos que están a la izquierda del terraplén.
6 CONLUSIONES
A pesar de que a simple vista las expresiones aquí
presentadas puedan parecer de tediosa aplicación,
es importante hacer notar que una vez
implementadas en una hoja de cálculo o en
cualquier lenguaje de programación, se dispondrá
de una herramienta que permita la rápida
determinación del incremento de esfuerzos en
cualquier punto del medio, facilitando así el cálculo
de asentamientos.
REFERENCIAS
Gray, H. (1936). “Stress distribution in elastic solids”,
Proceedings of the 1st International Conference
on Soil Mechanics and Foundation Engineering,
Vol. 2, pp. 157-168.
Jones, C. A.; Stewart, D. I. and Danilewicz, C. J.
(2008). “Bridge distress caused by approach
embankment
settlement”.
Geotechnical
Engineering, 161 (2), pp. 63-74.
Jürgenson, L. (1934). “The applications of elasticity
and plasticity to foundation problems”, Journal of
Boston Society of Civil Engineers, 21, 206.
Newmark, N. M. (1940). “Stress distribution in soils”,
Proceedings of the Purdue Conference on Soil
Mechanics and its Applications, pp. 295-303.
Osterberg J. O. (1957) “Influence values for vertical
stresses in a semi-infinite mass due to
embankment loading”. Proceedings of the 4th
International Conference on Soil Mechanics and
Foundation Engineering, Vol. 1, pp. 393–394.
Poulos, H. G. and Davis, E. H. (1974). Elastic
Solutions for Soil and Rock Mechanics, 1st
Edition, New York, John Wiley & Sons, Inc.
Tan, Y.C. & Gue, S.S. (2000) “Embankment over
Soft Clay – Design and Construction Control”,
Seminar on Geotechnical Engineering, September
2000, Penang.
5 COMENTARIOS
Es importante notar que en las ecuaciones (21) a la
(24), el valor de “z” no puede ser igual a cero, ya que
conduciría a una indeterminación. Esto se resuelve
simplemente asignándole a “z” un valor muy
pequeño cercano a cero tal como 10-5 m. De igual
forma “a” igual a cero conduciría a una
indeterminación en las ecuaciones (30), (31) y (32).
Aunque este problema puede ser resuelto de la
misma forma que para “z” igual a cero, “a” igual a
cero implicaría una carga rectangular, por lo que no
tendría sentido el utilizar las soluciones aquí
presentadas. También es importante resaltar que “z”
SOCIEDAD MEXICANA DE INGENIERÍA GEOTÉCNICA A.C.