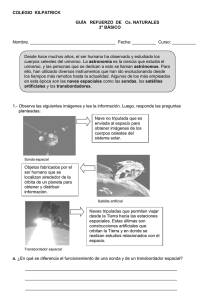
Sonda espacial
Anuncio

Departamento: Física Aplicada III Mecánica Racional (Ingeniería Industrial) Curso 2007-08 Sonda espacial. Y P Γ ρ Una sonda espacial, considerada como punto material P de masa m, se mueve en el plano OXY (sistema de referencia inercial) cuyo origen O coincide con el centro de un planeta. Este ejerce sobre la sonda una fuerza de atracción gravitatoria JJJG G G G G G F (r ) = −(mK / ρ 2 ) u ρ , siendo OP = r = ρ u ρ el θ A radiovector que determina en cada instante la posición de la sonda respecto del centro del planeta. X Se pretende que, a partir de un punto A situado a O R0 una distancia R0 del punto O, la sonda se aproxime al planeta siguiendo una espiral logarítmica cuya ecuación en coordenadas polares es Γ ≡ ρ (θ ) = R0e − λθ , donde λ es una constante positiva Sonda espacial de valor conocido. Además, el módulo de su velocidad ha de disminuir progresivamente según la ley exponencial decreciente v(θ ) = v0e − λθ , siendo v0 el módulo de la velocidad de la nave en el punto A. G G G a) Determinar, en función de la distancia ρ, como ha de ser la fuerza Φ = Φ (r ) que han de aplicar los motores de la sonda espacial durante la maniobra de aproximación. b) Calcular la energía consumida durante la maniobra por dichos motores si estos se apagan cuando la nave se encuentra próxima a la superficie del planeta, a una distancia r0 de su centro O. Solución Análisis previo Se trata de un problema plano con dos grados de libertad descritos por las coordenadas independientes ρ, θ (polares). El sistema no es conservativo porque aunque la fuerza gravitatoria es conservativa, la que ejercen los motores no lo es. Por otra parte no se trata de un movimiento central, porque aunque la fuerza gravitatoria si es del tipo central (centro O), la de los motores no lo es. En consecuencia los teoremas de conservación del momento cinético y de la energía no aportan integrales primeras del movimiento. El problema se resolverá aplicando el segundo principio de la Dinámica. a) Fuerza de los motores G Como las expresiones que se dan en el enunciado vienen dadas en función de ρ y de u ρ , utilizaremos coordenadas polares. Aplicaremos la segunda ley de la dinámica donde G G G F + Φ = ma . G G G ) uθ a = ( ρ − ρθ 2 )u ρ + ( ρθ + 2 ρθ (1) (2) Los componentes de la aceleración se calcularán a partir de la ecuación de la trayectoria y del dato sobre la velocidad. Esta magnitud se expresa G G G v = ρ u ρ + ρθ uθ Para obtener las derivadas temporales necesitamos θ , que se obtendrá del módulo de la velocidad v = ρ 2 + ρ 2θ 2 ρ = −λ R0e− λθθ ; ρ = −λ ρθ v = λ ρ θ + ρθ ; 2 2 2 2 v = ρθ (λ + 1) 2 (3) Dinámica del punto material Problema: Sonda espacial Podemos expresar el el módulo de la velocidad en función de ρ: v(θ ) = v= v0 ρ R0 θ = v0 R0 v0 R0 e − λθ R0 (4) Igualando se obtiene 1 λ2 +1 cte (5) Mediante esta expresión y la regla de la cadena podemos obtener las derivadas temporales de ρ Derivado ρ respecto del tiempo ; ρ = − λρθ ρ = λ 2 ρθ 2 Con ello podemos calcular los componentes aρ = ρ − ρθ 2 = (λ 2 − 1) ρθ 2 , = 2 ρθ = −2λρθ 2 aθ = ρθ + 2 ρθ Despejando de (1) se obtiene la expresión de la fuerza que ejercen los motores, G ⎛ K λ 2 − 1 v02 ⎞ G 2λ v02 G m ρ uθ Φ=⎜ 2 + 2 ρ ⎟ mu ρ − 2 2 2 R R + + ρ λ λ 1 1 0 0 ⎝ ⎠ b) Energía consumida durante la maniobra de aproximación La fuerza calculada anteriormente no es conservativa, sin embargo podemos calcular el trabajo realizado mediante el teorema de la energía: W ' = Δ (T + U ) donde U es la energía potencial de la fuerza gravitatoria debida a la atracción del planeta r0 ΔU = − ∫ − R0 Km G G G u (uρ d ρ + uθ ρ dθ ) ; 2 ρ ρ r0 Km R0 ρ2 ΔU = ∫ dρ ; ⎛1 1 ⎞ ΔU = − Km ⎜ − ⎟ ⎝ r0 R0 ⎠ 1 2 Teniendo en cuenta (4) , la variación de energía cinética vale ΔT = m v02 2 1 2 r0 − mv0 2 R02 Con todo ello resulta W'= ⎛ r2 ⎞ ⎛1 1 ⎞ 1 m v02 ⎜ 02 − 1⎟ − Km ⎜ − ⎟ 2 ⎝ R0 ⎠ ⎝ r0 R0 ⎠ Mecánica Racional (Ingeniero Industrial) pg. 2/2