Diagramas de Radiación
Anuncio

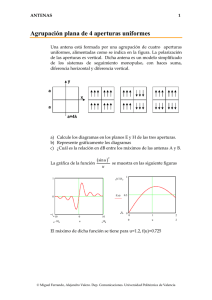
ANTENAS 1 Diagramas de Radiación La expresión para la Densidad de Potencia radiada por una antena es de la forma 2 sin ( 2.5π sin θ ) π Pmax θ ≤ 2 ( 2.5π sin θ ) P (θ , φ ) = π 0 θ> 2 a) b) c) d) Calcule la dirección del máximo de radiación Represente gráficamente el diagrama en los planos XZ,YZ,XY Calcule el ancho de haz entre ceros y a –3dB del corte XZ Obtenga el nivel de lóbulo principal a secundario Diagrama de radiación El diagrama también se puede expresar como sin ( u ) P ( u ) = Pmax u = 2.5π sin θ ( u ) La representación gráfica de la función es 2 1 1 0.8 0.6 F( u) 0.4 0.2 0 0 10 − 10 5 0 u 5 10 10 El máximo se encuentra en u=0, es decir en la dirección del eje z (è=0). Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 2 Diagramas de radiación Los planos XY,XZ,YZ corresponden en coordenas esféricas a Plano XY XZ YZ Ángulo è 0<è<ð 0<è<ð è =ð /2 Ángulo Ö Ö =0, ð Ö =ð /2, 3ð /2 0< Ö <2ð Se puede observar que el diagrama no depende del ángulo Ö, por lo tanto tendrá simetría en torno al eje z y el diagrama en el plano XY será omnidireccional. Los valores de u estarán acotados: u = 2.5π sin θ 0 ≤ u ≤ 2.5π Los nulos del diagrama de radiación se tendrán para u = 2.5π sinθ 0 = π , 2π 2 θ 0 = arcsin = 23.6 0 5 4 θ 0 = arcsin = 53.10 5 En el plano XY el diagrama es constante. La representación gráfica para los semiplanos XZ,YZ es z 1 0.9 0.8 0.7 0.6 P( θ ⋅deg) 0.5 0.4 0.3 0.2 0.1 0 0 15 30 45 60 75 90 θ Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 3 Ancho de haz entre ceros y –3dB 2 La posición del primer cero del diagrama es θ 0 = arcsin = 23.6 0 5 2 El ancho de haz entre ceros será el doble ∆θ 0 = 2arcsin = 47.2 0 5 Para determinar el ancho de haz a –3dB hay que determinar el valor en el que sin ( u−3 ) P P ( u−3 ) = max = Pmax ( u ) 2 −3 2 u = 1.39 El ángulo en el que la densidad de potencia es la mitad será 1.39 0 θ −3 = arcsin = 10.2 2.5 π y el ancho de haz a –3dB será el doble 20.4 0 Nivel de lóbulo principal a secundario El diagrama de radiación tiene el máximo en la dirección del eje z sin ( 0) P ( 0 ) = Pmax = Pmax ( 0 ) El primer cero aparece en u=ð, y el primer l óbulo secundario se encuentra aproximadamente en u=3ð/2 2 2 3π 2 sin 2 3π 2 P = Pmax = Pmax 2 3π 3π 2 El nivel de lóbulo principal a secundario es P NLPS = 10log max = 13.4 dB Psec Si no se realiza ningún tipo de aproximación , obteniendo una tabla de valores de la función sin u 20log u se puede observar que el valor exacto es 13.2 dB Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia