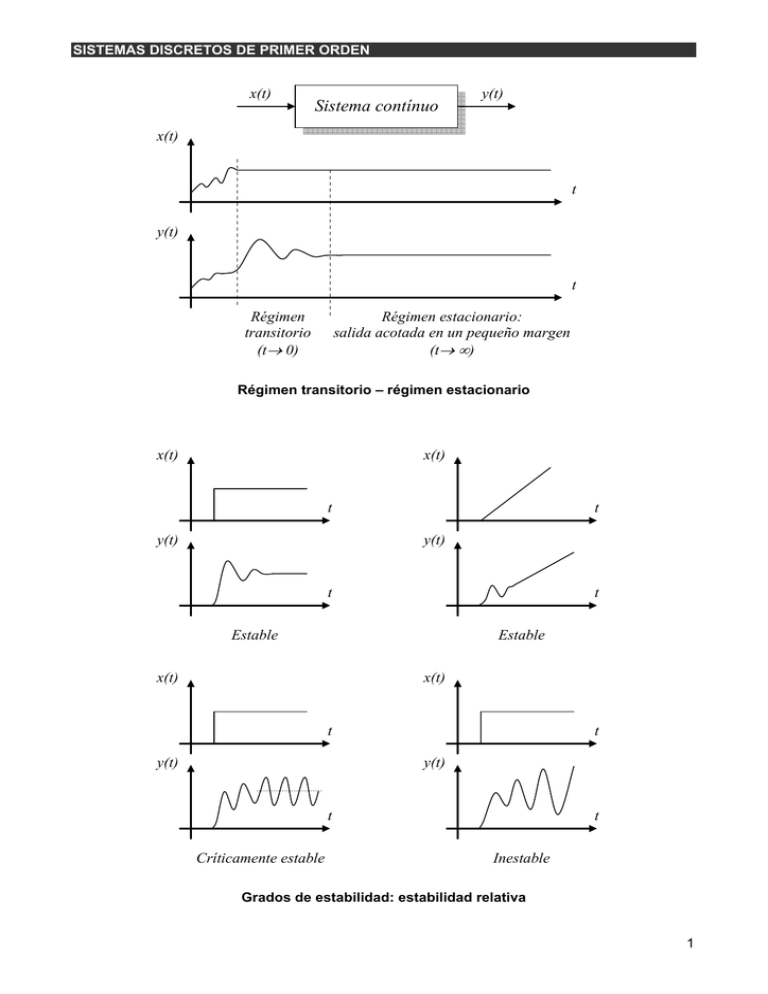
Sistema contínuo

SISTEMAS DISCRETOS DE PRIMER ORDEN
x(t)
Sistema contínuo
y(t)
x(t)
t
y(t)
t
Régimen
transitorio
(t→ 0)
Régimen estacionario:
salida acotada en un pequeño margen
(t→ ∞)
Régimen transitorio – régimen estacionario
x(t)
x(t)
t
y(t)
t
y(t)
t
t
Estable
Estable
x(t)
x(t)
t
y(t)
t
y(t)
t
Críticamente estable
t
Inestable
Grados de estabilidad: estabilidad relativa
1
SISTEMAS DISCRETOS DE PRIMER ORDEN
x(t)
t
y(t)
Sobreoscilación
Respuesta B
1,05K
0,95K
K
Error de
posición
Respuesta A
t
Tiempo de establecimiento
Régimen transitorio
Régimen
estacionario
B es más estable que A
Especificaciones de funcionamiento para la salida
Im(s)
Im(z)
Re(s)
s = α ± β·j ∈C
Zona donde deben estar los
polos de la función
transferencia de un sistema
para que sea estable
1
|z|
Re(z)
z = a ± b·j ∈C
Estabilidad en el plano z (transformada Z para sistemas discretos)
en relación con el plano s (transformada de Laplace para sistemas continuos)
2
SISTEMAS DISCRETOS DE PRIMER ORDEN
x(k)
y(k)
yk = a·yk-1 + b·xk
X(z)
G( z) =
Y(z)
b· z
z−a
Sistema de primer orden
g(k)
Im(z)
a2
b
a1
a2
a1
0
Re(z)
1
2
3
4
5
6
7
8
k
1
y(k)
a1
b
1 − a
b
0
1
2
3
4
5
6
7
8
k
Polos y respuestas del sistema cuando a>0
g(k)
Im(z)
b
a3
k
-b
a4
a3
a4
Re(z)
0
1
1
2
3
4
5
6
7
8
g(k)
b
b/(1-a)
a3
k
0
1
2
3
4
5
6
7
8
Polos y respuestas del sistema cuando a<0
3
SISTEMAS CONTINUOS DE SEGUNDO ORDEN
G( s) =
x(t)
X(s)
y(t)
Y(s)
G(s)
K ·ωn2
s 2 + 2·ζ ·ωn ·s + ωn2
=
K ·ωn2
( s + σ − ωd j )( s + σ + ωd j )
s 2 + 2·ζ ·ωn ·s + ωn2 = 0 → s1,2 = −ζ ·ωn ± ωn · 1 − ζ 2 j
σ = ζ ·ωn
⎫⎪
⎬ → s1,2 = −σ ± ωd j
ωd = ωn · 1 − ζ 2 ⎪⎭
Sistema continúo de segundo orden
Im(s)
ωn
s1
ωd j
α
Re(s)
-σ
cos α =ζ
s2
-ωd j
Polos complejos conjugados de un sistema continúo de segundo orden
y(t)
yp
tr =
Mp
1,05K
0,95K
K
0,9K
π −α
tp =
ωd
π
ts ≈
0,1K
t
tr
Mp =
ωd
π
σ
yp − K
=e
K
−
·100 =
σ ·π
ωd
·100
tp
ts
Respuesta temporal a un escalón del sistema continúo de segundo orden
4
SISTEMAS DISCRETOS DE SEGUNDO ORDEN
x(k)
X(z)
yk + a· yk −1 + b· yk − 2 = c· xk
y(k)
Y(z)
G(s)
G( z) =
c· z 2
z 2 + a·z + b
Sistema discreto de segundo orden
Im(z)
Polo de G(z) en notación polar:
p1
Im(p1)
p1 = e −σ
⎫
−σ θ j
⎬ → p1 = e ·e
∠p1 = θ = e ⎭
/p1-1/
/p1/
θ
θj
γ
Re(z)
1
Re(p1)
p2
Polos complejos conjugados de un sistema discreto de segundo orden
A
A
⎧
e− k ·σ sen(k ·θ − γ ) k ≥ 1
+
⎪
y (k ) = ⎨1 − 2e −σ cos θ + e−2σ
p1 − 1 e−σ sen θ
⎪
k≤0
0
⎩
y(k)
Mp
1,05K
0,95K
ys
k
kr
kp
ks
Respuesta temporal a una secuencia escalón del sistema discreto de segundo orden
5
SISTEMAS DISCRETOS DE SEGUNDO ORDEN
ωn
s1
Im(s)
Im(z)
ωd j
Im(p1)
α
cos α =ζ
/p1/
θ
Re(s)
-σ
s2
p1
Re(z)
Re(p1)
Z = eT·s
-ωd j
p2
s1,2 = −ζ ·ωn ± ωn · 1 − ζ 2 j = −σ ± ωd j
T −σ ±ωd j )
z1,2 = eT ·s = e (
= e −Tσ e±T ·ωd j
z1 = e −Tσ = Re( z1 ) + Im( z1 )
2
∠z1 = θ = T ·ωd = arctg
2
Im( z1 )
Re( z1 )
Relación entre los polos de un sistema continúo de segundo orden y uno discreto
Im(s)
Im(z)
Re(s)
Estabilidad
Im(s)
Im(z)
ωd1
ωd2
Valores de ωd
constantes
Re(s)
ωd3
Re(z)
1
ωd1·T
ωd2·T
Re(z)
ωd3·T
Correspondencia entre un sistema continúo de segundo orden y uno discreto (I)
6
SISTEMAS DISCRETOS DE SEGUNDO ORDEN
Im(s)
Im(z)
Valores de σ
constantes
e σ2·T
1
Re(s)
σ1
σ2
e σ1·T
Im(s)
ζ1
Im(z)
α1
ζ2
Valores de ζ
constantes
α2
Re(z)
Re(s)
ζ1
ζ2
Re(z)
1
cos αi =ζ i
ζ2 > ζ1
Im(s)
Im(z)
Valores de ωn
constantes
ωn1
ωn2
Re(s)
ωn1
ωn2
Re(z)
Correspondencia entre un sistema continúo de segundo orden y uno discreto (II)
7
SISTEMAS DISCRETOS DE SEGUNDO ORDEN
Correspondencia entre un sistema continúo de segundo orden y uno discreto (III)
8
SISTEMAS DISCRETOS DE SEGUNDO ORDEN
r(k)
R(z)
e(k)
E(z)
u(k)
U(z)
Gc(z)
u(t)
U(s)
H(s)
G(s)
Bloqueador
(D/A)
Controlador
y(k)
Y(z)
y(t)
Y(s)
Planta
T
Ge(z)
A/D
Ge ( z ) = Ζ
{L
−1
{H (s)·G(s)}}
Sistema de control digital directo
r(k)
R(z)
e(k)
E(z)
G(z)=Gc(z)·Ge(z)
y(k)
Y(z)
F.T. de bucle abierto
Sistema de control digital directo simplificado (con realimentación unitaria)
E( z) =
1
1 + G( z)
(
R( z )
)
e∞ = lim e(k ) = lim 1 − z −1 E ( z )
k →∞
z →1
(
e∞ = lim 1 − z −1
z →1
) 1 + G1 ( z) R( z)
1
z
⎧
Secuencia
escalón
1,1,1,1,...
Z
=
=
⎡
⎤
{
}
⎣
⎦
⎪
1-z −1 z − 1
⎪
R( z ) = ⎨
T ·z
⎪ Secuencia rampa Z ⎡⎣{0, T , 2T ,3T ,...}⎤⎦ =
⎪⎩
( z − 1)2
Cálculo del error en régimen estacionario con el teorema del valor final
9
SISTEMAS DISCRETOS DE SEGUNDO ORDEN
e∞ = e p =
y(k)
1
1+ Kp
ep
K p = lim G( z )
z →1
r(k)
kT
Error cuando la entrada es la secuencia escalón o “error de posición”
en un sistema de tipo 10
e∞ = ev =
T
ev
Kv
r(k)
Kv = lim ( z − 1) G( z )
z →1
y(k)
kT
Error cuando la entrada es la secuencia rampa o “error de velocidad”
en un sistema de tipo 1
Tipo
ep
1
ev
∞
0
1+ Kp
1
0
2
0
0
3
0
0
…
0
0
T
Kv
Tabla resumen de los errores para cada tipo de sistema
10