Tabla de Transformadas de Laplace δ
Anuncio
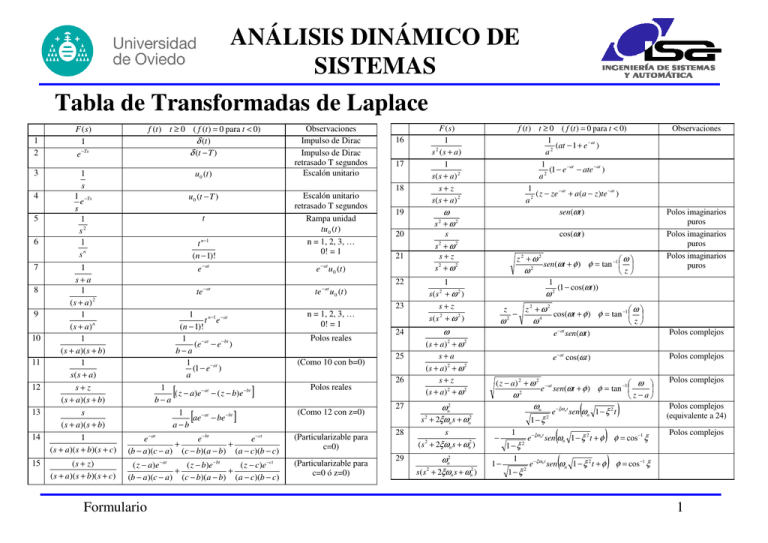
ANÁLISIS DINÁMICO DE SISTEMAS Tabla de Transformadas de Laplace F (s) 1 e −Ts f (t ) t ≥ 0 ( f (t ) = 0 para t < 0) δ (t ) δ (t − T ) 3 1 s u 0 (t ) 4 1 −Ts e s 1 s2 1 sn u 0 (t − T ) 1 2 5 6 7 8 9 10 11 12 13 14 15 Observaciones Impulso de Dirac Impulso de Dirac retrasado T segundos Escalón unitario 16 17 18 Escalón unitario retrasado T segundos Rampa unidad tu 0 (t ) n = 1, 2, 3, … 0! = 1 t t n−1 (n − 1)! − at e u 0 (t ) te − at te − at u 0 (t ) 20 21 e − at e− bt e− ct + + (b − a )(c − a) (c − b)(a − b) (a − c)(b − c) (Particularizable para c=0) (s + z) ( s + a )( s + b)( s + c) ( z − a)e − at ( z − b)e − bt ( z − c)e −ct + + (b − a )(c − a) (c − b)(a − b) ( a − c)(b − c) (Particularizable para c=0 ó z=0) 23 n = 1, 2, 3, … 0! = 1 Polos reales (Como 10 con b=0) 1 ( z − a)e− at − ( z − b)e −bt b−a 1 ae− at − be −bt a −b [ [ Formulario ] ] Polos reales (Como 12 con z=0) cos(ωt ) s s + ω2 s+z 2 s + ω2 2 22 1 t n−1 e − at (n − 1)! 1 (e− at − e− bt ) b−a 1 (1 − e− at ) a ω s +ω2 2 − at 1 s+a 1 (s + a) 2 1 (s + a) n 1 ( s + a)( s + b) 1 s ( s + a) s+z ( s + a)( s + b) s ( s + a)( s + b) 1 ( s + a)( s + b)( s + c) e 19 f (t ) t ≥ 0 ( f (t ) = 0 para t < 0) 1 (at − 1 + e − at ) a2 1 (1 − e −at − ate −at ) a2 1 ( z − ze − at + a (a − z )te −at ) a2 sen(ωt ) F (s ) 1 s 2 (s + a) 1 s( s + a) 2 s+z s( s + a) 2 24 26 27 ω2 1 s(s 2 + ω 2 ) s+z s( s 2 + ω 2 ) z ω 2 z +ω2 − ω4 29 ω cos(ωt + φ ) φ = tan −1 z − at e sen(ωt ) Polos complejos e− at cos(ωt ) Polos complejos 2 ( s + a) + ω s+a ( s + a) 2 + ω 2 s+z ( s + a) 2 + ω 2 ω Polos imaginarios puros Polos imaginarios puros Polos imaginarios puros ω 2 ( z − a) 2 + ω 2 ω2 ω e − at sen(ωt + φ ) φ = tan −1 z −a ωn 2 n s 2 + 2ξωn s + ωn2 28 ω sen(ωt + φ ) φ = tan −1 z 1 (1 − cos(ωt )) 2 ω 2 25 z2 + ω2 Observaciones 1− ξ 2 s ( s 2 + 2ξωn s + ωn2 ) − ωn2 s ( s 2 + 2ξωn s + ωn2 ) 1− 1 1−ξ 2 1 1− ξ 2 ( e−ξω nt sen ωn 1 − ξ 2 t ) ( ) φ = cos−1 ξ ( ) φ = cos−1 ξ e−ξω nt sen ωn 1 − ξ 2 t + φ e−ξω n t sen ωn 1 − ξ 2 t + φ Polos complejos Polos complejos (equivalente a 24) Polos complejos 1 ANÁLISIS DINÁMICO DE SISTEMAS Sistemas de Primer Orden (I) K G(s) = 1 + T ·s X(s) G(s) g(t) y(t) K/T Y(s) x(t) y(t) K: ganancia estática o en régimen permanente T: constante de tiempo 0,37·K/T Tangente en el origen (pendiente K/T) y(t) • Respuesta impulsional: X(s)=1 K 0,95·K −t K y (t ) = L [Y ( s )] = L [G ( s )] = e T ·u0 (t ) T −1 t T −1 0,63·K • Respuesta a un escalón: X(s)=1/s T t 3·T −t G ( s) T y (t ) = L−1[Y ( s )] = L−1 = K ·( 1 − e )·u0 (t ) s y(t) T (pendiente K) • Respuesta a una rampa: X(s)=1/s2 −t G (s) y (t ) = L [Y ( s )] = L 2 = [ K ·(t − T ) + K ·T ·e T ]·u0 (t ) s −1 −1 t T -K·T Formulario 2 ANÁLISIS DINÁMICO DE SISTEMAS Sistemas de Segundo Orden (I) Si a,b>0, el sistema es estable K ·ω n2 K Ks G ( s) = 2 = = 2 1 2 2·ξ s + 2·ξ ·ω n ·s + ω n2 s + a·s + b · s + · s + 1 2 ωn 2 2 n s + 2·ξ ·ω n ·s + ω = 0 Las raíces del polinomio (polos del sistema) son : s1, 2 = −ξ ·ω n ± ω n · ξ 2 − 1 Si ξ < 1 las raíces son complejas ωn K: ganancia estática T=2·ξ/ωn: constante de tiempo ξ>0: coeficiente de amortiguamiento ωn>0: frecuencia natural del sistema σ>0: constante de amortiguamiento o factor de decrecimiento Si ξ<1, ωd : frecuencia amortiguada conjugadas : σ = ξ ·ω n ω d = ω n · 1 − ξ 2 s1, 2 = −σ ± j·ω d ωn -σ Im ωd θ ξ = cosθ Re -ωd Formulario 3 ANÁLISIS DINÁMICO DE SISTEMAS Sistemas de Segundo Orden (II) Sobreoscilación : −π ·ξ Mp =e 1−ξ 2 −π ·σ ·100[%] = e ωd ·100[%] = e −π ·cotgθ ·100[%] = Tiempo de subida : tr = π −θ = ωn 1 − ξ 2 π −θ ωd y(t) 1 M = r 2·ξ · 1 − ξ 2 si 0 < ξ < 0.707 2 ω r = ω n · 1 − 2·ξ ← Pico de Resonancia ← Frecuencia de Resonancia B− A ·100[%] A Pico de sobreoscilación B Ritmo de decrecimiento Tiempo de pico : tp = π ωn 1 − ξ = 2 π ωd A 0.9·A A±5% Entrada en régimen permanente Tiempo de establecimiento : ts = π π = ξ ·ω n σ (aprox.) 0.5·A Régimen transitorio Tiempo de retardo : 1+ td = ξ 2 ωn Régimen permanente 0.1·A (aprox.) Formulario td tr tp 2·π 3·π 4·π ωd ωd ωd ts t 4 ANÁLISIS DINÁMICO DE SISTEMAS Criterio de Estabilidad de Routh Indica si existen raíces con parte real positiva en un polinomio: El sistema que tenga como denominador ese a0 ·s n + a1 ·s n−1 + a2 ·s n−2 + ... + an−2 ·s 2 + an−1 ·s + an = 0 polinomio, será estable 1) ∀ai, ai>0 (es decir, todos con el mismo signo y sin nulos) si todos los ai>0 y todos 2) Se construye la siguiente tabla: los coeficientes de la a1 ·a2 − a0 ·a3 1 a0 a 2 b1 = =− primera columna de la s n a0 a2 a4 a6 ... a1 a1 a1 a3 tabla son también a a s n−1 a1 a3 a5 a7 ... a ·a − a ·a 1 4 b2 = 1 4 0 5 = − 0 estrictamente positivos. s n−2 s n−3 ... s2 s1 s0 b1 b2 c1 c2 ... ... u1 u 2 v1 w1 Formulario b3 c3 ... b4 c4 ... ... a1 a1 a5 a1 ·a6 − a0 ·a7 1 a =− 0 a1 a1 a1 a6 a7 a1 b3 = ... b1 ·a3 − a1 ·b2 1 a a = − 1 3 b1 b1 b1 b2 b ·a − a ·b 1 a a c2 = 1 5 1 3 = − 1 5 b1 b1 b1 b3 c1 = El polinomio tiene tantos polos con parte real positiva como cambios de signo se producen en la primera columna de la tabla 5