Revisión de conceptos básicos en estadística I.
Anuncio

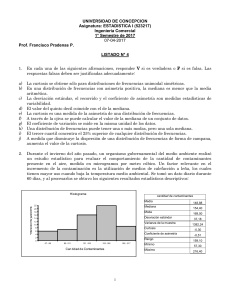
Jacobo Trébol López Dr Juan José de la Cruz (D-35). EPI. CLIN. 2-. REVISIÓN DE CONCEPTOS BÁSICOS EN ESTADÍSTICA 1: 0)-. DEFINICIÓN BIOESTADÍSTICA: Ciencia que estudia la obtención y condiciones de aplicación de determinados procedimientos que resuelvan científicamente el problema de recoger, organizar y analizar datos procedentes de la observación de fenómenos biológicos. Por sus procedimientos es una ciencia matemática (la ciencia de las probabilidades, nunca seguridad), por su naturaleza una ciencia aplicada y por su objetivo una ciencia metodológica. Representa la herramienta fundamental para la investigación biológica dado que nos da las reglas para: -formulación de hipótesis. -análisis de resultados. -obtención de conclusiones a partir de los anteriores. En esta y la próxima clase nos centraremos sobre todo en los dos últimos apartados a través de: -estadística descriptiva: se encarga de estructurar la información referente al fenómeno o experimento estudiado en la población de estudio. -estadística univariante: tipo de análisis que compara variables 2 a 2. -estadística multivariante: en este caso suele requerir un n grande y una metodología compleja (ejemplo colesterol frente a hábitat ajustado por edad). Los dos primeros se realizan siempre, el último es opcional. A)-. RECUERDO CONCEPTOS ESTADÍSTICOS 1-. POBLACIÓN, ELEMENTO Y CARACTERES Población: todo estudio estadístico ha de estar referido a un conjunto o colección de personas o cosas que denominamos población. La población puede ser según su tamaño de dos tipos: o Finita: Ej: número de alumnos de un centro de enseñanza, o grupo de clase. o Infinita: el número de elementos que la forman es infinito, o tan grande que pudiesen considerarse infinitos. Como por ejemplo si se realizase un estudio sobre los productos que hay en el mercado, hay tantos y de tantas calidades que esta población podría considerarse infinita. Denominamos N al tamaño de la población (número de elementos). Elementos o unidades muestrales: cada uno de los componentes que forman parte de la población. Muestra: representa un subconjunto de la población total con el cual podemos trabajar operativamente (la población no siempre es fácilmente accesible ni mucho menos económicamente accesible). n (minúscula) es el tamaño de la muestra. Caracteres o variables: cada elemento de la población tiene una serie de características o cualidades que pueden ser objeto de estudio estadístico. Así, por ejemplo, si consideramos como elemento a una persona, podemos distinguir en ella los siguientes caracteres: sexo, edad, nivel de estudios, profesión, peso, altura, color de pelo... Modalidad o categoría: cada uno de los posibles valores numéricos o descriptivos de 1 carácter. Ej para color de pelo rubio, moreno,… 1 2-. CONSIDERACIONES GENERALES SOBRE MUESTREO: Partimos de una población y queremos estudiar en ella un carácter. Para ello seleccionamos una muestra y después extrapolaremos a la población las conclusiones mediante el uso de estimadores (inferencia estadística o generalización). En este proceso hay 2 pasos trascendentales: -selección de la muestra: debe ser representativa de la población: número suficiente (para la magnitud de la diferencia que queremos demostrar según los errores que asumamos como muy bien debeis saber ya en 6º ) y además necesito que sus características sean muy parecidas a las de la población en unas variables que pueden influir y que pueden estar descritas (ej: TA y sexo, edad, hábitat) o no. Pero esto por supuesto me aumentará n. El ser tan complejo hace que haya muchas fórmulas y variantes de cálculo y selección. -estimación: usar estimadores con errores estándares,… Los tipos de parámetros estadísticos con los que trabajamos en cada nivel son: -población: media poblacional μ, varianza poblacional σ2, error estandar de la media (eem),… -muestra: media muestral (x con sombrero), varianza muestral S2n , cuasivarianza muestral S2n-1 y las estimaciones puntuales. 3-. TIPOS DE VARIABLES Y SUS REPRESENTACIONES GRÁFICAS 1)-. Cualitativas Describen cualidades de los elementos de la muestra. Ordinales: pueden establecerse con cierto orden (clase social, categorías de IMC). Nominales: categorías excluyentes y sin orden (sexo, HTA si/no). Deben ser universales: con las distintas categorías englobo toda la población. Las gráficas que mejor las definen son: o Diagramas de barras. o Gráficas de sectores (tartas o quesitos). 50 40 30 n 20 10 0 Varones 45% Alta Media Mujeres 55% Baja Clase social Puedo poner en el eje de abscisas también porcentajes. 2)-. Cuantitativas / numéricas 25 Frecuencias relativas acumuladas Devuelven valores numéricos para cada caso. Continuas: siempre existe un valor intermedio entre dos valores (talla). Discretas: sólo pueden tomar determinados valores (personas con fiebre, número de hijos aunque esta frecuentemente se toma como cuali). Gráficas: o Histogramas (pictograma: dibujo como un lápiz y polígonos de frecuencias). o Polígonos de frecuencias acumuladas. 20 15 n 10 5 1 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0 140 150 0 160 170 180 190 Talla (cm) Talla (cm) 200 2 B)-. ESTADÍSTICA DESCRIPTIVA: Para llevar a cabo la correcta descripción de una variable en la muestra debemos especificar siempre n y frecuencias (variables cualitativas y cuantitativas discretas) y para las continuas cuantitativas lo más importante son las medidas de localización (o posición) o tendencia central y medidas de dispersión o variabilidad. 1-. CUALITATIVAS Y CUANTITATIVAS DISCRETAS Frecuencia absoluta (ni): número de casos en cada categoría. Frecuencia relativa (fr): proporción de casos en cada categoría (tanto por 1). fr = ni / N (es decir el cociente entre ni y el tamaño muestral). Representa la probabilidad de pertenecer a una de esas categorías. Frecuencia porcentual (%): porcentaje en cada categoría. % = fr x 100 Razón (r): expresa una relación cuando las magnitudes son independientes. Ej: número de casos de un grupo entre los de otro distinto. Frecuencia absoluta acumulada (Ni) Suma de las frecuencias absolutas de las modalidades inferiores o iguales a xi. Frecuencia porcentual acumulada (Fi) Suma de las frecuencias relativas de las modalidades iguales o inferiores a xi. En este ejemplo se puede ver fácilmente cómo se calculan estas frecuencias. Personas Activas Número Familias Xi 1 2 3 4 Total ni 16 20 9 5 50 de fi 16/50 20/50 9/50 5/50 %i 32% 40% 18% 10% Ni 16 36 45 50 Fi 16/50 36/50 45/50 50/50 %i 32% 72% 90% 100% 2-. CUANTITATIVAS: 1-. MEDIDAS DE TENDENCIA CENTRAL Valor al que tienden a agruparse los datos. Media aritmética (x): suma de valores entre número de casos. x = i=1n Xi / n Mediana (Me): valor observado que, ordenados los valores de forma creciente, divide el número de casos en dos partes iguales. Es útil cuando hay gran asimetría, valores extremos. 50% Me 50%. Ej: es la mejor variable para calidad de vida y supervivencia. Moda (Mo): valor observado que tiene mayor ni (que más se repite). No tiene mucho interés. Se utiliza para ver por qué la distribución se hace bimodal. 2-. MEDIDAS DE DISPERSIÓN Miden la variabilidad o dispersión de los datos. Rango o amplitud (R): diferencia entre el valor máximo observado y el valor mínimo en la muestra. R= Máx - Mín Rango intercuartílico (Q3-Q1): si dividimos los valores de la muestra organizados de menor a mayor en 100 partes iguales tenemos los percentiles. Un percentil es el valor que deja % “i” de casos a su izquierda. Los cuartiles son cuartos de esta distribución de 3 valores (percentiles 25, 50, 75). Q1 deja por debajo el 25% valores y Q3 el 75 % luego Q3-Q1 me indica el rango del 50% central. Análogamente podemos definir el P15-P85 que coge el 70% de la distribución. Estas tres anteriores son válidas sobre todo para variables que no son bien descritas por la media (distribución no normal). Varianza (2): mide la distancia entre los valores y la media estimada. 2 = S2 = (xi - x )2 / n Desviación típica (): es la raíz cuadrada de la varianza. No es buena medida de dispersión si la distribución es asimétrica, en tal caso la medida de tendencia central mejor será la mediana y no la media (que sería buena si la distribución fuera continua). Es la medida más frecuentemente empleada en distribuciones normales. Coeficiente de variación (CV): se usa para comparar distribuciones. Suele expresarse en % (x100). CV= / x NOTA: Una distribución normal se representa como x +/- . Una distribución no normal se representa como Me +/- rango o rango intercuartílico. 3-. MEDIDAS DE FORMA: Son medidas de la forma de la distribución. No siempre se realizan. Permiten sobre todo conocer la descripción de gráficas de distribución de frecuencias. 3.1. Medidas de simetría: La simetría es importante para saber si los valores de la variable se concentran en una determinada zona del recorrido de la variable. Coeficiente de asimetría de Pearson: As= x - Mo / x Coeficiente de asimetría de Fisher: As = (x - x )3ni/N/x3 As<0 As=0 As>0 Asimetría Negativa a la Izquierda Simétrica Asimetría Positiva a la Derecha. 4 3.2-. Medidas de aplastamiento: coeficiente de Curtosis Analiza el grado de concentración que presentan los valores alrededor de la zona central de la distribución. Se definen 3 tipos de distribuciones según su grado de curtosis: El coeficiente de Curtosis viene definido por la siguiente fórmula: g2 = (1/n)x (xi-xm)4x ni -3 Si sale 0 la distribución es mesocúrtica, si mayor de 0 leptocúrtica y si menor de 0 platicúrtica ((1/n)x(xi-xm)4x ni))2 C) DISTRIBUCIÓN NORMAL: La mayoría de las variables aleatorias que se presentan en los estudios relacionados con las ciencias sociales, físicas y biológicas, por ejemplo, el peso de niños recién nacidos, talla de jóvenes de 18 años en una determinada región, son continuas y se distribuyen según una función de densidad, que tiene la siguiente expresión analítica : 1 x 2 1 2 f ( x) e 2 Donde μ es la media de la variable aleatoria y σ es su desviación típica. Este tipo de variables se dice que se distribuye normalmente. El área bajo la función de densidad es 1. La función de densidad, en el caso de la distribución Normal, tiene forma de campana : Aquí añado un par de conceptos del año pasado, que no los he incluido antes porque están muy sueltos: 5 o Error muestral (error estándar): mide la dispersión de los estadísticos de todas las posibles muestras de la población. o Intervalo de confianza: valores entre los que se encuentra el valor medio de la población con una probabilidad p. 6