Tema 2 Dado el vector r que divide al segmento AB en la razón
Anuncio
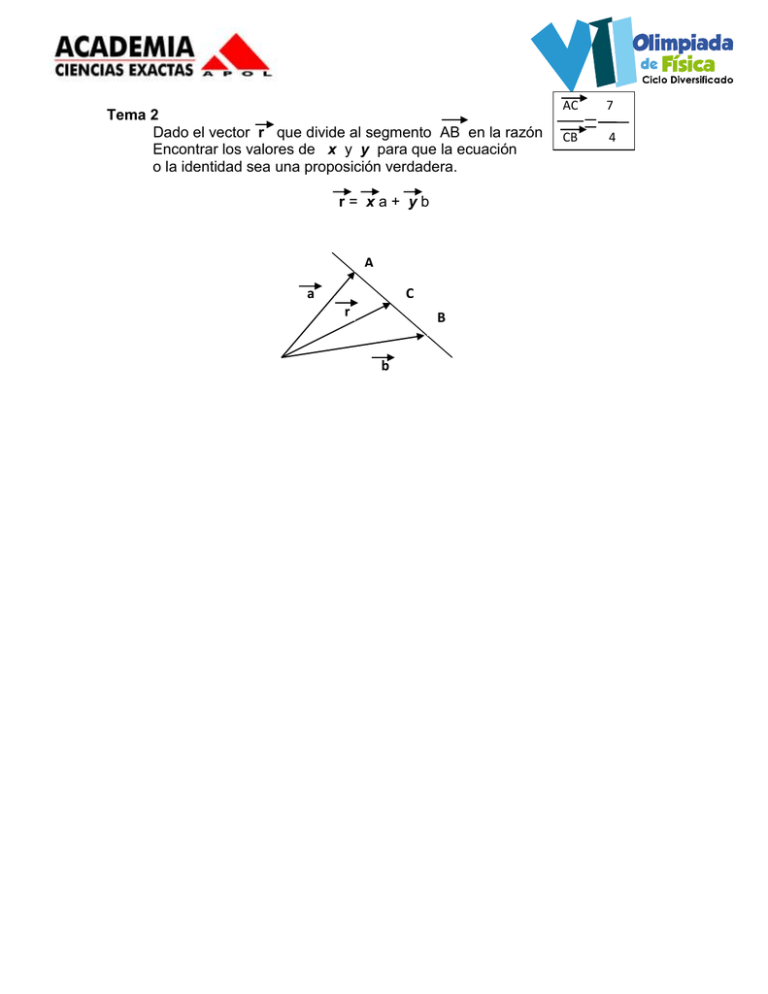
Tema 2 Dado el vector r que divide al segmento AB en la razón Encontrar los valores de x y y para que la ecuación o la identidad sea una proposición verdadera. r= xa+ yb A a C r B b AC 7 CB 4 Tema3 El siguiente gráfico muestra la variación de la velocidad v con respecto al tiempo t de un objeto moviéndose en línea – recta V 0 t 0 ¿Cuál de las siguientes gráficas representa mejor el cambio de la aceleración a con respecto al tiempo t? A. B.- a a 0 t 0 0 C.- t 0 D.- a a 0 0 0 t 0 Tema 4 Los dos bloques mostrados en la figura parten del reposo. El plano horizontal y la polea no tienen rozamiento y se supone que la polea es de masa despreciable. Determínese la aceleración de cada bloque y la tensión en cada cuerda. Tema 5 ¿Qué velocidad mínima debe tener la bola de masa m en el punto A para que pueda llegar hasta el punto B siguiendo la trayectoria curva (es decir, describiendo un arco de circunferencia de radio R) de la figura, sin desprenderse y suponiendo que no hay rozamiento en ningún punto de la trayectoria. Al final sustituye h= 1.5 R para obtener la velocidad pedida en función de g y R. Tema 6 Una barcaza con masa 1.50 X 105 kg, avanza rio abajo a 6.20 m/s entre niebla espesa, cuando choca de costado contra otra que cruza el rio horizontalmente. La segunda barcaza tiene una masa de 2.78 X 10 5 kg y se desplazaba a 4.30 m/s. Inmediatamente después del impacto, su curso se desvia 18.0º rio abajo y su rapidez aumenta a 5.10 m/s. La corriente era prácticamente cero en el momento del accidente. ¿Qué rapidez y dirección de movimiento tendrá la primera barcaza de inmediato después de la colisión? Tema7 Una escalera uniforme que pesa 200N esta reclinada contra una pared. La escalera se desliza cuando Ѳ = 60°. Suponiendo que los coeficientes de fricción estática entre la pared y el suelo son los mismos, obtenga un valor para µ Tema 8 Un anillo de cobre de 21.6 g tiene un diámetro de 2.54000 cm a la temperatura de 0oC. Una esfera de aluminio tiene un diámetro de 2.54533 cm a la temperatura de 1000 C La esfera se situa sobre el anillo, y se deja que ambos lleguen al equilibrio térmico, sin que se disipe calor alguno al entorno. La esfera pasa justamente a través del anillo a la temperatura de equilibrio. Halle la masa de la esfera. CCU= 387 J/KgK 2.54533cm CAl= 900 J/KgK αCU= 17X 10-6/°C αAl= 23X 10-6/°C 00C Cu 2.54000cm Tema 9 Un bloque de madera flota en el agua sobresaliendo de la superficie 5 cm. Cuando se pone en glicerina, de densidad relativa 1.35, sobresalen 7.5cm de la superficie del líquido. Determinar la densidad relativa de la madera Tema 10 Tres cargas de valores Q1 =2 µC, Q2 = 2 µC y Q3 desconocida, están en el plano XY en los puntos Q1: (1,0), Q2: (-1,0) y Q3: (0,2), en metros. Determinar el valor de Q3 para que la fuerza sobre una carga situada en (0,1) sea nula. Tema 1 Un hito importante en la evolución del universo, justo después de la gran explosión es el tiempo planck tp. Cuyo valor depende de tres constantes fundamentales: Velocidad de la luz C = 3 x 108 m/s Constante de gravitación de Newton G= 6.67 X 10-11 m3/Kgs2 Constante de Planck h = 6.63 x 10-34 Kgm2/s Haciendo que el tiempo de Planck dependa de estas constantes tp = ci Gj hk donde i, j y k son exponentes a determinar, con base en un análisis dimensional. Escriba la expresión resultante, y encuentre el valor del tiempo Planck. Unidad S. I. Dimensión Longitud Masa Tiempo Rapidez Aceleración Densidad m L kg M s T m/s L/T m/s2 L/T2 kg/m3 M/L3











