Pag. 1 PROGRAMACIÓN LINEAL
Anuncio

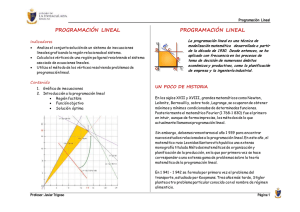
Pag. 1 PROGRAMACIÓN LINEAL Aquí verás cómo los sistemas de desigualdades vistos antes te pueden ayudar para optimizar algunas cantidades. La programación Lineal es una técnica matemática que se utiliza para solucionar los más diversos problemas ( de transporte, dieta, producción, etc) en que se desea optimizar (al máximo o al mínimo) una situación factible de expresarse como una función lineal de dos ó más variables, la cuál está sujeta a cierto número de restricciones, que corresponden a inecuaciones lineales. A continuación resolveremos problemas de dos variables, utilizando la técnica de la Programación Lineal. Para resolver un problema mediante esta técnica, es necesario determinar: La Función Objetivo: la representación algebraica de la situación que se busca optimizar. Esta Función Objetivo se designa como: F(x,y) = ax + by ; a, b . El conjunto de restricciones lineales para las variables que intervienen en la Función Objetivo y que conforman un sistema de inecuaciones lineales. Ejemplo1: Un problema de maximización En una industria se fabrican artículos, A y B, los cuales deben pasar por los procesos P1, P2 y P3 para su elaboración. La fabricación del artículo A requiere de 6 horas en P1, 4 horas en P2 y ninguna en P3. En cambio, la fabricación del artículo B demora 5 horas en P1, 7 horas en P2 y 8 horas en P3. En los procesos P1, P2 y P3 se pueden trabajar como máximo 40, 36 y 32 horas a la semana, respectivamente. Desarrollo: La Función Objetivo está determinada por la relación lineal existente entre la utilidad po cada artículo y la cantidad que se fabrica de él. Si la utilidad que se obtiene por cada artículo A es de $8.000 y por cada artículo B, de $26.000, se quiere determinar la cantidad óptima de producción semanal de cada artículo, para obtener una utilidad máxima. Como puedes ver, los datos de un problema de esta naturaleza son los numerosos, y conviene organizarlos en un cuadro como el siguiente: P1 P2 P3 Utilidad A 6 4 0 8.000 B 5 7 8 26.000 Tiempo máximo 40 36 32 El siguiente paso del desarrollo del problema consiste en designar las variables: Sea x = Cantidad de artículos A que se van a producir y = Cantidad de artículos B que se van a producir De acuerdo con los datos del problema, la maximización de la ganancia está dada por la optimización de la Función Objetivo siguiente: F (x,y) =8.000 x + 26.000 y El conjunto de las restricciones lineales, para las variables x, y está dado por el número de horas que toma su elaboración. P1 : 6x + 5y 40 P2 : 4x + 7y 36 P3 : 8y 32 Además debe cumplirse que: x 0, y 0; ya que el número de artículos que se fabrican no puede ser negativo. A continuación veremos como encontrar la solución de este problema por medio del denominado método gráfico. Resolver un problema de programación lineal consiste en determinar un par (x,y) de números reales que satisfaga todas las desigualdades del sistema y optimice la Función Objetivo. La resolución de un problema de programación lineal se apoya en el siguiente teorema: Pag. 2 Teorema Fundamental: “ Si existe una solución que optimice la función objetivo, esta debe encontrarse en uno de los vértices de la región determinada por las restricciones del problema “ Entonces para determinar la solución del problema por el método gráfico, se siguen los siguientes pasos: Se determina gráficamente la región solución del sistema de inecuaciones interceptando los semiplanos de cada inecuación. Esta región se llama región factible. Se determinan las coordenadas (x,y) de cada vértice de la región factible. Se reemplazan los valores (x,y) de cada vértice en la función objetivo. Se selecciona un vértice que determine el valor óptimo. Las coordenadas de este vértice son los valores que optimizan el problema, es decir, el par (x,y) es la solución del problema. Continuemos entonces, resolviendo el problema planteado anteriormente. Maximicemos la Función Objetivo F (x,y) =8.000 x + 26.000 y Sujeta a las restricciones: 6x + 5y 40 4x + 7y 36 8y 32 x 0 y 0