Veamos ahora lo que debe suceder al hacer girar la prepa
Anuncio

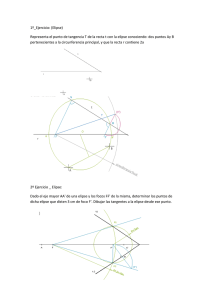
62 ANALES DE HISTORIA NATURAL. (22) Veamos ahora lo que debe suceder al hacer girar la p r e p a ración, ó lo que es lo mismo, al hacer girar un poro alrededor de su centro; y para ello partamos de la posición de coincidencia entre las secciones principales de los nicoles y los ejes de la elipse directriz, fijándonos solamente, para mayor sencillez, en el brazo vertical de la cruz. Si se efectúa el giro de derecha á izquierda, esto es, al contrario del movimiento de lasag-ujas de un reloj, el eje mayor de la elipse directriz (fig. 12) que en la posición inicial coincidía con la sección del analizador A A', se encontrará en a a' después de haber girado la cantidad angular A o a. Es evidente que las moléculas situadas sobre el eje menor b b', y que antes de empezar el giro estaban en condiciones de extinción de luz, no lo están ahora. ¿Lo estarán las que se encuentran sobre el diámetro í v, que coincide con la sección PP' del polarizador? Tampoco, por las razones que se van á exponer. Para hallar la fila de moléculas cuyos ejes de elasticidad sean perpendiculares y paralelos á la s e c ción PP' del polarizador, y que por lo mismo producirán obscuridad, es preciso determinar el punto de la elipse cuya t a n gente sea perpendicular á PP' y unirlo con el centro o y esta línea, ó mejor este diámetro de la elipse directriz será la p o sición que habrá tomado el brazo vertical de la cruz después del giro A o a. Para ello basta recordar que la tangente en el extremo de un diámetro es paralela á su diámetro conjugado, y por lo tanto, para hallar el punto de la elipse directriz cuya tangente es perpendicular á PP', ó lo que es lo mismo, p a r a lela al diámetro m n, bastará trazar su conjugado r s, y éste marcará la posición del brazo vertical de la cruz puesto que todas las moléculas sobre él situadas tienen sus ejes de elasticidad perpendiculares y paralelos á PP'. El ángulo mor que forman los dos diámetros conjugados m 11 y r s es por necesidad obtuso, y, por lo tanto, la línea r o s, que es ahora el brazovertical de la cruz, no coincide con PP' sino que está desviada hacia la derecha, en dirección contraria á la del giro de la preparación, lo que está conforme con lo que realmente s u cede (1). (]) Tal vez no estará de más recordar que se llaman, en Geometría analítica, d i á metros conjugados de la elipse, «dos diámetros tales que cada uno biseca las cuerdasparalelas al otro», y que, «la tangente en la extremidad de un diámetro es paralela á,