S_ntesis_de_la_Geometr_a_Anal_tica
Anuncio

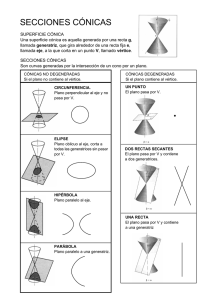
LA GEOMETRÍA ANALÍTICA Conceptos básicos: Punto: Es la representación de una posición fija del espacio. No es un objeto físico, es decir, carece de forma y dimensiones. Los puntos se localizan en un plano cartesiano o plano de coordenadas, haciendo que una coordenada sea un punto, una ubicación en X y Y. Recta: Puede describirse como la sucesión continua e indefinida de puntos en una sola dimensión, sin tener un principio o fin. Se extiende en una misma dirección y está compuesta de infinitos segmentos. Esto podemos observarlo en las gráficas lineales. Puede ser definida por dos puntos a los que une recorriendo su menor distancia. Hay tres formas algebraicas para representar una recta. 1. Y=mx+b 2. mx+nb=b 3. forma general: Ax+Bx+c=0 Plano: Superficie reglada generada por el movimiento de una generatriz (g), que se mantiene en contacto con una directriz (d) recta, siendo paralelas todas las posiciones de la generatriz. Esto viene siendo un plano cartesiano, el cual sirve para localizar puntos que nos den coordenadas específicas. Esto es lo que se usa en los radares, donde dan la posición exacta de un objeto. Secciones Cónicas: El estudio de las cónicas es de gran importancia en los campos de la óptica, astronomía, física, biología, informática e ingeniería, entre otras, ya que son la base del diseño de lentes, espejos, y superficies elípticas, circulares parabólicas e hiperbólicas. Son componentes esenciales de: microscopios, telescopios, radares, antenas parabólicas, teodolitos, distanciómetros y muchos otros instrumentos de gran uso en estas ciencias, pues es aquí donde tienen su aplicación estas secciones. 0 0 Parábola: Se forma cuando a =b . Es el conjunto de todos los puntos de un plano que son equidistantes de un punto fijo llamado foco y de una recta fija llamada directriz. Este término incluso se utiliza en física fundamental, al realizar tiro parabólico. La expresión algebraica que describe una parábola que ocupe cualquier posición en un plano es: ax² + bxy +cy² +dx + ey + ƒ =0 Hipérbola: Se forma cuando a0>b0. Es el lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos llamados focos es constante. Ecuación de una hipérbola con centro en el punto h , k (x-h)²/a² - (y-k)²/b² = 1 Elipse: Se forma cuando a0<b0. Es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante. No importa la ubicación de un punto en la elipse, pues al sumar las distancias al punto "A" al punto "B", siempre saldrá lo mismo. La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es: x²/a² + y²/b² = 1