Reguladores de cancelación
Anuncio

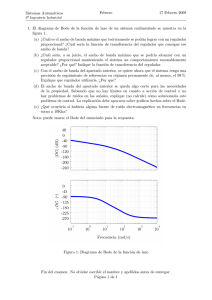
Práctica de Diseño de Sistemas Avanzados de Control: método de cancelación Abel Alberto Cuadrado Vega 24 de abril de 2007 1. Introducción Se trata de obtener un regulador C(z) para el control de un sistema G(z) obteniéndose un sistema en cadena cerrada M (z). El lazo de control tiene la siguiente estructura: R(z) E(z) U(z) C(z) G(z) Y(z) - y se denotarán los polinomios de numeradores y denominadores de las funciones de transferencia como: G(z) = B(z) A(z) C(z) = Q(z) P (z) M (z) = N (z) L(z) (1) y donde A(z) tiene grado n, B(z) tiene grado m, P (z) tiene grado d, Q(z) tiene grado c, L(z) tiene grado ν y N (z) tiene grado µ. 2. Método de cancelación Se trata de obtener el regulador C(z) simplemente partiendo de la relación de realimentación: C(z)G(z) M (z) = (2) 1 + C(z)G(z) en la que despejando C(z) se obtiene: C(z) = M (z) G(z)[1 − M (z)] 1 (3) y sustituyendo todos los polinomios de numeradores y denominadores y operando, queda: A(z)N (z) C(z) = (4) B(z)[L(z) − N (z)] Se observa que por tener el regulador a A(z) en el numerador como factor, en principio, éste cancela todos los polos de G(z). Análogamente, por tener el regulador a B(z) en el denominador como factor, en principio, éste cancela todos los ceros de G(z). Nótese que este método (en principio) nos permite elegir tanto los ceros como los polos deseados para M (z) (cadena cerrada). 3. Consideraciones en la aplicación del método de cancelación A la hora de aplicar este método hay que tener en cuenta ciertas cuestiones relacionadas con la implementación real de las soluciones. 3.1. Realización fı́sica A la hora de elegir el sistema que se quiere obtener en cadena cerrada, hay que asegurarse de que tanto éste como el regulador obtenido son realizables fı́sicamente (causales). Ası́, si imponemos que el regulador obtenido a partir de (4) sea causal, los grados de los polinomios deben cumplir: gr(A) + gr(N ) ≤ gr(B) + gr(L − N ) (5) Si también imponemos causalidad en M (z), el grado de L(z) será mayor o igual que el de N (z) y por lo tanto la resta de estos dos polinomios nunca será de mayor grado que el de L(z): gr(L) ≥ gr(N ) ⇒ gr(L − N ) ≤ gr(L) (6) con lo que podemos sustituir en la primera relación gr(L − N ) por gr(L) y se sigue cumpliendo: gr(A) + gr(N ) ≤ gr(B) + gr(L) (7) y operando se llega a: gr(A) − gr(B) ≤ gr(L) − gr(N ) (8) que dice que la diferencia de grados entre denominador y numerador de M (z) tiene que ser mayor o igual que la de G(z), es decir, que el tiempo muerto de M (z) tiene que ser mayor o igual que el de G(z). 3.2. Estabilidad El regulador obtenido no debe cancelar ceros ni polos fuera de la circunferencia unidad porque la cancelación en la realidad nunca es exacta. Analizando la situación con el lugar de las raı́ces se puede deducir que con una de estas falsas cancelaciones se crea una rama entre el cero y el polo que da lugar a un polo inestable en cadena cerrada. Por lo tanto en la obtención del regulador deben imponerse condiciones para evitar estas cancelaciones. 2 4. 4.1. Enunciado de la práctica Obtención del regulador Realizar un programa Matlab para obtener un regulador por el método de cancelación, particularizando para el control del sistema con función de transferencia: 335 G(s) = 2 (9) s + 10,3s + 134 de tal forma que se obtenga un tiempo de pico tp = 100 ms, una sobreoscilación Mp = 10 % y un error nulo ante entrada. Usar un periodo de muestreo T m elegido según el criterio (redondeado a las milésimas): Tm = 2π 30ωn (10) donde ωn es el ancho de banda del sistema realimentado. Representar gráficamente con Matlab para el sistema realimentado resultante: Respuesta a escalón unitario de la salida (para comprobar que cumple las especificaciones). Respuesta a escalón unitario de la acción de control (para determinar qué escalón máximo se le puede introducir sin que la acción de control salga del rango ±5 y sature). Mapa de polos y ceros de la función de transferencia de cadena cerrada antes de aplicarle minreal y después (para hacer patentes las cancelaciones). NOTA: No cancelar el cero de G(z) que aparece a la frecuencia de Nyquist (cero real y negativo). ¿Qué le ocurre a la acción de control si se cancela? Funciones útiles de Matlab: conv (multiplicación de polinomios), minreal (eliminación de la función de transferencia de polos y ceros que se cancelan), dcgain (ganancia estática de un sistema), pzmap (mapa de polos y ceros de un sistema), pole (polos de un sistema), zero (ceros de un sistema). 4.2. Prueba experimental Probar experimentalmente el programa anterior aplicándolo al control del módulo electrónico de segundo orden, siguiendo los siguientes pasos: 1. Ajustar los parámetros del sistema Mp y ωn con los potenciómetros en su punto medio. 2. Conectar la salida del módulo amplificador con la entrada del sistema de segundo orden. 3. Colocar las sondas del osciloscopio en la entrada del amplificador (la de ganancia variable) y en la salida negada del sistema de segundo orden, que serán respectivamente la entrada y la salida del sistema a controlar G(s). 3 4. Ajustar la ganancia del amplificador de forma que el sistema a controlar tenga ganancia K = 2,5. Esto se puede hacer fácilmente poniendo 2 V/división en el canal de la entrada y 5 V/división en el canal de salida y haciendo que ante entrada cuadrada de periodo suficientemente largo se superpongan las dos señales para el régimen permanente. 5. Identificar el sistema, sustituir la función de transferencia G(s) del apartado anterior por la resultante y recalcular el regulador. 6. Comprobar que el control con dicho regulador cumple exactamente tanto las especificaciones del transitorio como del régimen permanente. 7. Observar cómo se ven afectados el transitorio y el permanente al disminuir la ganancia del amplificador, y especialmente el permanente cuando en dicha situación concurre otra de las dos siguientes: Los coeficientes del regulador se han tomado de manera que al coger un número limitado de decimales (los que dé el Matlab al sacar la función de transferencia en pantalla), los coeficientes del denominador de la función de transferencia suman cero. Idem sin sumar cero (forzar, si es necesario, modificando en una unidad el último dı́gito del a2 ). 4