Trabajo Práctico 6
Anuncio

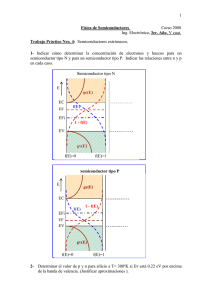
1 Física de Semiconductores Curso 2008 Ing. Electrónica, 3er. Año, V cuat. Trabajo Práctico Nro.6: Guía teórico-práctica: Juntura PN. Objetivos: Estudiar el comportamiento físico de una juntura PN abrupta. Obtener resultados numéricos, órdenes de magnitud de parámetros y comparar resultados. Introducción: Hasta ahora hemos estudiado los fenómenos físicos básicos que controlan las propiedades de los semiconductores. A partir de ahora veremos cómo utilizar estos conocimientos para entender el funcionamiento de estructuras más complejas denominadas junturas. Las junturas son uniones entre materiales. Las mismas pueden realizarse entre semiconductores de diferentes características (Juntura PN), entre semiconductores y metales (Juntura MetalSemiconductor) o entre semiconductores, metales y aislantes (Juntura Metal-AislanteSemiconductor). Las junturas constituyen las estructuras básicas de cualquier dispositivo electrónico discreto, formado por un dispositivo único, o de un circuito integrado formado por miles de dispositivos interconectados sobre un mismo chip1. La figura muestra una fotografía de un circuito integrado formado por miles de junturas. A continuación se presenta como diferentes tipos de junturas se utilizan en el desarrollo de dispositivos electrónicos de uso corriente. 1 Un circuito integrado (CI) es un circuito electrónico realizado completamente sobre una cara de una delgada pieza de silicio de un solo cristal al que los fabricantes denominan "pastilla" o "chip". 2 Tipos de junturas Semiconductor- Semiconductor homojunturas Metal- Semiconductor heterojunturas Uniones del mismo material Uniones de diferentes materiales Diodo Schottky Contacto rectificante Una sola juntura Diodo rectificador Más de una juntura Metal- Aislante- Semiconductor Diodo túnel Diodo Zener Diodos Transistores Diodo varicap Fotodiodo Diodo emisor de luz Diodos de microondas Transistor bipolar de unión BJT Transistor de efecto de campo de juntura JFET Rectificador Controlado de Silicio SCR Transistor bipolar de puerta aislada IGBT Otros Diodo Schottky Contacto óhmico Capacitor MIS Transistor de efecto de campo de puerta aislada MOSFET Estructura CMOS (MOS Complementaria) 3 1- Formación de una juntura PN Una juntura PN se forma cuando se ponen en contacto regiones de tipo P y de tipo N de un mismo material semiconductor (homojuntura) o de materiales semiconductores diferentes (heterojunturas), figura 1. En principio, estudiaremos una juntura PN de silicio. La interface que separa las regiones P y N se denomina unión metalúrgica. En realidad, este contacto no puede ser realizado colocando en forma adyacente un material con otro debido a la discontinuidad que se produciría. Según la forma en que se realiza la transición desde la región P a la región N, las junturas pueden clasificarse en: abruptas y graduales. La juntura abrupta es aquella en la cual la transición se realiza en una distancia muy corta. Para la juntura gradual la distancia es mayor. Región tipo P Región tipo N P N Contacto y electrodo Unión metalúrgica Figura 1 Generalmente, la juntura PN se obtiene cambiando el dopaje del material de tipo N a tipo P (o viceversa) por diferentes procesos: el proceso de difusión durante el crecimiento de la muestra cristalina o el proceso de implantación iónica. En el proceso de difusión, figura 2, se calienta el silicio a una temperatura muy alta en una atmósfera que contiene el compuesto del elemento que ha de agregarse, por ejemplo Boro, para crear una dopaje tipo P. A temperaturas altas el Boro se descompone y se deposita sobre el silicio. Algunos átomos se difunden sobre la superficie sustituyendo átomos de silicio, moviéndose hacia el interior del cristal. Cuando se enfría se forma una delgada capa de silicio de tipo P cuya profundidad puede controlarse variando el tiempo, la temperatura (900 ºC - 1100 ºC) y la atmósfera para la difusión. En la implantación de iones, figura 3, se utiliza un haz de iones de energía muy alta (30 - 100 keV) que bombardea directamente el cristal. El potencial de aceleración controla la profundidad de implantación. Este método proporciona un mejor control de la distribución del contaminante y en general, se emplea para producir uniones poco profundas. T ~ 900ºC - 1100ºC Haz de iones B+ de alta energía Flujo de gas con compuesto de Boro Oblea de silicio Cámara de vacío Oblea de silicio Figura 3 Figura 2 La distribución del contaminante en función de la profundidad recibe el nombre de perfil de contaminación. 4 2- Principio básico de operación La figura 4 muestra un esquema de la juntura PN y de la concentración de impurezas en las regiones P y N, para el caso de una juntura abrupta uniformemente dopada. Inicialmente, al ponerse en contacto los materiales y sin polarización externa aplicada, en la zona de unión metalúrgica hay un gradiente de concentración de electrones y huecos. P N NA ND Difusión de huecos Difusión de electrones x x=0 Figura 4 Los electrones, portadores mayoritarios en la región N tenderán a difundirse hacia la región P, y los huecos, portadores mayoritarios en la región P se difundirán hacia la región N. Sin embargo, este proceso no puede continuar en forma indefinida. Cuando los electrones se difunden hacia la región P dejan átomos donadores cargados positivamente. Del mismo modo, los huecos que se difunden hacia la región N dejando átomos aceptores cargados negativamente. La diferencia de carga neta positiva y negativa induce un campo eléctrico en la región cercana de la unión y dirigido desde la carga positiva hacia la negativa, es decir, desde la región N a la región P, figura 5. Impurezas ionizadas (NA) Impurezas ionizadas (ND) Región N neutra Región P neutra P Fuerza de difusión sobre los huecos - - - - - - - - - - + + + + + + + + + + + + Región de carga espacial N Fuerza de difusión sobre los electrones Campo eléctrico E Componente de deriva sobre los huecos Componente de deriva sobre los electrones Figura 5 La región en la cual se produce el campo eléctrico se denomina región de carga espacial. Los electrones y los huecos son barridos por el campo eléctrico hacia afuera de la región de carga espacial, dejando esta zona desprovista de portadores móviles, y por ello se la suele denominar zona o región de agotamiento. 5 Puede considerarse que el gradiente de concentración en los bordes de la región de carga espacial produce una fuerza de difusión sobre los portadores. El campo eléctrico E en esta región produce una fuerza de deriva sobre los portadores opuesta a la fuerza de difusión, de modo que en el equilibrio las dos fuerzas tenderán a equilibrarse provocando que, sin polarización externa, la corriente neta que circula sea nula, y el nivel de Fermi sea continuo en todo el sistema. Lo anterior puede expresarse a través de las siguientes relaciones para huecos y electrones respectivamente, y del diagrama de bandas de energía resultante de la unión en equilibrio, figura 6. dp Jp q p p E - Dp 0 dx dn Jn q n n E Dn 0 dx P EC N e q Vbi EFi EC EF (EF - EFi)P EF EV (EF - EFi)N h EFi q Vbi EV Figura 6 Las bandas de conducción y de valencia se curvan en la región de carga espacial porque hay un cambio en la posición del nivel de Fermi intrínseco entre las regiones P y N. Los electrones en la banda de conducción de la región N ven una barrera de potencial de altura (q Vbi) cuando tratan de moverse hacia la banda de conducción de la región P. Lo mismo ocurre con los huecos en la banda de valencia. La altura de esta barrera de energía potencial es igual a la suma de las diferencias entre el nivel de Fermi respecto al nivel intrínseco en cada región (P y N). El potencial de la barrera se denomina potencial de contacto Vbi (built-in potential barrier) y está dado por: Vbi kT NA ND ln q ni2 ND y NA son las concentraciones de impurezas en las zonas N y P respectivamente. 3- Análisis de la región de carga espacial: aproximación de vaciamiento El principio físico que gobierna el comportamiento eléctrico en la región de carga espacial es el teorema de Gauss que relaciona el campo eléctrico con la concentración de carga espacial. Para un tratamiento unidimensional queda expresado por: dE dx 6 donde E es el campo eléctrico, la concentración de carga espacial y es la permitividad dieléctrica del material semiconductor. El teorema de Gauss en la región de carga espacial puede expresarse como: dE q (N D - NA) dx porque en esta zona la carga de las impurezas inmóviles (NA, ND) domina la concentración de carga. Como el campo eléctrico se relaciona con el potencial en la forma: dV E(x) dx resulta la forma conocida como ecuación de Poisson: d 2V dx 2 - q (ND - NA) Para poder calcular las distribuciones de carga, campo eléctrico y potencial en la región de carga espacial suele utilizarse la aproximación de vaciamiento. Esta aproximación se basa en la hipótesis de que toda la capa de carga espacial está desprovista de portadores de carga móvil, es decir, huecos y electrones, de modo que la carga en esta zona está determinada solamente por la distribución de impurezas. La figura 7 compara la distribución real en la zona de carga espacial y la resultante de aplicar la aproximación de vaciamiento, para un caso general. Con esta aproximación hay una región de carga negativa debida a aceptores ionizados que se extiende desde la zona de unión hasta el punto xp en el lado P, y una región de carga positiva debida a donadores ionizados que se extiende desde el punto de unión hasta el punto xn sobre el lado N. El ancho total de la región de carga espacial w estará dado por w = x p + xn. Además, la carga total negativa y positiva tienen la misma magnitud de modo que se cumple: xp NA = xn ND Distribución real q ND Aproximación de vaciamiento -xp 0 xn x w - q NA Figura 7 4- Cálculo de campo eléctrico máximo y ancho de la región de agotamiento Se aplicará la aproximación de vaciamiento al caso mostrado en la figura 8. Se debe tener en cuenta que por neutralidad de la carga: xp NA = xn ND 7 Como puede verse de la figura 8, se tiene: (x) = 0 (x) = - q NA (x) = q ND (x) = 0 para - < x < -xp para -xp < x < 0 para 0 < x < xn para xn < x < + q ND xn -xp x xn x 0 - q NA xp x E x Emáx V Vbi x Figura 8 Se pretende encontrar una expresión para la altura de la barrera de potencial Vbi, el campo eléctrico máximo Emáx y el ancho de la región de carga espacial o de agotamiento w. El campo eléctrico se puede hallar aplicando el teorema de Gauss a la distribución de carga espacial. dE dx Integrando esta ecuación se obtiene una expresión para el campo eléctrico sujeta a las restricciones impuestas por las condiciones de contorno. El campo eléctrico debe anularse en x= - xp y x = xn porque en estos puntos se definen los límites de la región de agotamiento y además se considera campo eléctrico nulo en las regiones masivas. Si nos basamos en la definición de integral de una función como el área debajo de la curva definida por ésta, obtenemos directamente que el campo eléctrico resulte dado por el área de un rectángulo. Aplicando para x < 0 y considerando un x cualquiera: q NA E(x) x donde x = x - (-xp) 8 El campo aumentará linealmente con x llegando al valor máximo (Emáx) en el punto x= 0 (x = xp), resultando: q NA Emáx xp Cumpliendo con la condición de neutralidad de carga: q NA q ND Emáx xp xn Para x > 0 el campo eléctrico disminuye pues debe anularse en x = xn. Para calcular la altura de la barrera de potencial se considera la relación entre el campo eléctrico y el potencial dado por: dV Edx Aplicando un criterio similar al anterior para calcular la integral resulta que la altura de la barrera de potencial Vbi, es aproximadamente igual al valor, cambiado de signo, del área del triángulo que corresponde al campo eléctrico: 1 1 Vbi - Emáx (x n xp) - Emáx w 2 2 2 1 1 w Vbi q NA ND Emáx - 2q Vbi 1 1NA 1ND 5- Juntura PN con polarización inversa Con una polarización inversa VR, el lado P es más negativo que el N. P - - - - - - E - - - - + + + + + + + + + + + + N w ER - + N P EC EFi (EF - EFi)P EF EV Vo = Vbi + VR VR (EF - EFi)N EC EF EFi Vo = Vbi + VR EV Al campo eléctrico E en la región de carga espacial se suma el campo ER inducido por la tensión inversa VR. La estructura de bandas se modifica, y la altura de la barrera de potencial aumenta. 9 6- Juntura PN con polarización directa Va Con una polarización inversa Va, el lado P es más positivo que el lado N. El campo eléctrico E en la región de carga espacial tiene sentido opuesto al campo Ea inducido por la tensión directa Va. La estructura de bandas se modifica y la altura de la barrera de potencial disminuye. - - - - - - -E - - - - P + + + + + + + + + + + + N w Ea + - N P EC Vo = Vbi - Va EFi EF EV (EFi - EF)P EC EF Va (EF - EFi)N EFi EV Ejercicios propuestos: Ejercicio 1 Se tienen las siguientes muestras de silicio con las cuales se formará una juntura abrupta a T=300ºK: Si tipo P (NA) NA = 1017 cm-3 Si tipo N (ND) ND = 5x1016 cm-3 a) Calcular el nivel de Fermi respecto al nivel de Fermi intrínseco para cada material antes de la unión. Graficar el diagrama de bandas de energía. b) Dibujar el diagrama de bandas de energía al formarse la unión sin polarización externa aplicada. c) Explicar las condiciones físicas de juntura en equilibrio para polarización nula. ¿Qué sucede con el nivel de Fermi a lo largo del sistema? ¿Por qué se forma una barrera de energía potencial? ¿Qué es el potencial de contacto, Vbi (built-in potential barrier)? ¿De qué parámetros depende? Obtener una expresión que permita calcular el potencial de contacto y calcular su valor para los datos del problema. 10 Ejercicio 2 La aproximación de vaciamiento es un método que permite obtener los valores de la carga, el campo eléctrico y el potencial electrostático en la zona de carga espacial. Esta aproximación se basa en la hipótesis de que toda la capa de carga espacial esté desprovista o vacía de portadores de carga móviles, huecos y electrones. Toda la capa de carga espacial puede ser tratada como una capa de vaciamiento, es decir, una región en la cual la carga espacial viene determinada por la distribución de impurezas. a) Utilizando la aproximación de vaciamiento graficar la distribución de carga espacial (x), campo eléctrico E(x) y potencial V(x) en una juntura PN abrupta de Silicio en la cual NA=ND. b) Deducir las expresiones que permiten calcular xp, xn y w = xn+xp (ancho total de la región de agotamiento), el campo eléctrico máximo (Emáx) y el potencial (Vbi). Calcular los valores a T=300ºK si NA = ND = 1016 cm-3. c) Cómo se modificarán los gráficos obtenidos en a) si: NA << ND, ó NA >> ND. Sacar conclusiones. Calcular xp, xn, w, Emáx y Vbi para los siguientes casos: NA =1015 cm-3 , ND= 1017 cm-3 NA =5x1017 cm-3 , ND= 1015 cm-3 d) Comparando los resultados obtenidos verificar que cuando se realiza una juntura PN abrupta entre dos materiales semiconductores con un dopaje muy desigual, el ancho de la región de agotamiento w queda determinado por la concentración de impurezas del material menos dopado. Ejercicio 3 Un diodo de unión abrupta de Si se fabrica sobre un sustrato de tipo N (ND =1016 cm-3 ) sobre el que se difunde Indio para formar una región de tipo P (NA= 1018 cm-3). Calcular, justificando aproximaciones: a) las posiciones de los niveles de Fermi de las regiones N y P antes de la unión b) el potencial de contacto Vbi c) el ancho de las regiones de agotamiento N y P y el ancho total w. Ejercicio 4 Se tiene una juntura de GaAs uniformemente dopada a T=300ºK. Sin polarización, sólo el 20 por ciento de la región de carga espacial se encuentra en la región P. El potencial de barrera es Vbi = 1.2V. Determinar: NA, ND, xn, xp y Emáx. Justificar las aproximaciones que se realicen. (Obtener datos de tablas) Ejercicio 5 Un diodo de unión abrupta de silicio tiene un dopado NA = 1017 cm-3 y ND = 1015 cm-3. Si kT= 0.026 eV y ni = 1.5x1010 cm-3, calcular: 11 a) el potencial de contacto Vbi, xn, xp, w y el campo eléctrico máximo, sin polarización externa aplicada. b) Si se aplica un potencial externo V= -3V calcular los nuevos valores c) De los resultados del punto b) calcular el cambio en porcentaje en xn y w respecto del caso sin potencial externo. d) Dibujar aproximadamente la densidad de carga, campo eléctrico y potencial para las condiciones de polarización del punto b). e) Recalcular el punto a) para V= -5 V y V= -10 V. f) Comparar resultados y sacar conclusiones. Ejercicio 6 Se tiene una juntura abrupta ideal N+P de silicio. La relación de dopaje es ND = 50 NA , el potencial de barrera es Vbi = 0.752V y el máximo campo eléctrico es Emáx= 1.14x105 V/cm para una polarización inversa de 10V a T=300ºK. Determinar: NA, ND, xp. ( Justificar aproximaciones). Ejercicio 7 Se tiene una juntura abrupta de silicio a T = 300 °K con los siguientes datos: NA = 5x1015 cm-3 y ND = 1014 cm-3, ni = 1.5x1010 cm-3. Calcular: a) Vbi b) xn y xp para polarización nula. c) ¿Qué potencial inverso se tendrá que aplicar para tener x n = 30 m, si se considera que xp << xn ? Ejercicios para el alumno Ejercicio 1 Una juntura PN abrupta de Si con: NA= 4x1017 cm-3, ND=1016 cm-3, ni= 10x1010 cm-3, se encuentra a temperatura ambiente (kT/q=0.026V) sin polarización aplicada. Suponiendo válida la aproximación de vaciamiento calcular: a) El campo eléctrico en x=0, el potencial de contacto Vbi, xn, xp y w. b) Para los datos dados qué porcentaje de w corresponde a xn y cuál a xp? c) Dibujar en forma aproximada la densidad de carga y el campo eléctrico para los datos del problema. d) Dibujar el diagrama de bandas de energía indicando la posición del nivel de Fermi y la altura de la barrera de potencial. Ejercicio 2 Dada una juntura PN abrupta de silicio calcular, suponiendo válida la aproximación de vaciamiento: a) la altura de la barrera de energía potencial (Eo), el potencial de contacto (Vbi), el 12 campo eléctrico máximo (Emáx), el ancho de la región de agotamiento (w) y los valores de xn y xp, si se aplica un potencial externo de valor V= -2 V para los siguientes casos: a1) NA = ND = 1015 cm-3 a2) NA = 1017 cm-3 y ND = 1014 cm-3 a3) NA = 1014 cm-3 y ND = 1017 cm-3 Comparar los resultados numéricos obtenidos y graficar densidad de carga, campo eléctrico y potencial. b) ¿Cómo se modificarían los resultados anteriores si se aplica un potencial externo de valor V= -10 V?. Comparar resultados y sacar conclusiones. Ejercicio 3 Una juntura abrupta de silicio P+N debe ser diseñada de modo que para una polarización inversa de 10V el máximo campo eléctrico sea Emáx = 106 V/cm. Determinar cuál deberá ser la concentración de dopaje de la región N. (T=300ºK). Justificar aproximaciones. Bibliografía sugerida: El diodo de unión PN - G. Neudeck Dispositivos semiconductores, J. Singh Semiconductor physics & devices- D. Neamen, Cap. 6 Electrónica física y modelos de circuitos de transistores (Cap. 2) -S.E.E.C. vol. 2