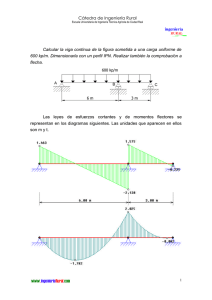
Determinar el ancho b de una viga de sección rectangular, de canto
Anuncio

Cátedra de Ingeniería Rural Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real Determinar el ancho b de una viga de sección rectangular, de canto h=20 cm, con el criterio de que la flecha en el extremo del voladizo sea δc=1 cm. La carga es de 2.5 t/m, y el módulo de elasticidad vale E=2⋅106 kg/cm2. 2.5 t/m A B C 2m 6m Figura 1. Viga biapoyada con un voladizo. La deformada de la viga se muestra en la figura 2: Figura 2. Deformada real de la viga. Forzando el diagrama para facilitar su estudio, se tiene: C' C A θ B A' l B C0 l/3 Figura 3. Análisis del problema. 1 Cátedra de Ingeniería Rural Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real En primer lugar se calcula el ángulo girado por B. Para ello se aplica Mohr entre A y B. θB = AA ' δ AB = = L L ∫ L 0 M ⋅ x ⋅ dx [1] E ⋅I L Para obtener el momento, se analiza el esquema de la figura 4. Para hacer más genéricos los cálculos, los valores numéricos se sustituyen por su variable representativa. Así, q=2.5 t/m y L=6 m. 2.5 t/m A B x C x' RA RB Figura 4. Diagrama para la obtención de momentos. ∑M B RA = = 0 → RA ⋅ L − q ⋅ L ⋅ L L L + q⋅ ⋅ = 0 2 3 6 4 ⋅ q ⋅L 9 Por tanto, M = 4 q⋅ x2 ⋅ q⋅L ⋅ x − . Introduciendo este valor en [1], se 9 2 obtiene el valor de δAB: 4 q ⋅ x2 ⋅ q ⋅ L ⋅ x − ∫0 9 2 = E ⋅I L δ AB ⋅ x ⋅ dx 5 q ⋅ L4 = ⋅ 216 E ⋅ I 2 Cátedra de Ingeniería Rural Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real Al ser δAB>0, el punto A está situado por encima de la tangente en B, y por ello el ángulo girado será en sentido contrario a las agujas del reloj, tal y como se muestra en la figura 2, de valor: 5 q ⋅ L3 θB = − ⋅ 216 E ⋅ I El enunciado nos da la deformación del punto C. Así, atendiendo a la notación de la figura 3, se tiene: δ C = C 0 C = 1 cm = C 0 C' − CC' Al haber calculado el ángulo girado por B (θB), la determinación de la magnitud C 0 C' es sencilla, pues se realiza por triangulación. Así, C 0 C' = θ B ⋅ L 5 q ⋅ L4 = ⋅ 3 648 E ⋅ I Por último, sólo falta calcular la distancia CC' , y para ello se aplica de nuevo Mohr entre B y C, pues corresponde a la deformada de C respecto a la tangente trazada por B. Así: δ CB ∫ = L/3 0 M ⋅ x'⋅dx ' E ⋅I q ⋅ x' 2 Entre B y C el momento se expresa por M = − 2 Operando, se tiene: δ CB = ∫ L/3 0 − q ⋅ x' 2 ⋅ x'⋅dx ' − 1 q ⋅ L4 2 = ⋅ E ⋅I 648 E ⋅ I Por tanto, 1 cm = 5 q ⋅ L4 1 q ⋅ L4 1 q ⋅ L4 ⋅ − ⋅ = ⋅ 648 E ⋅ I 648 E ⋅ I 162 E ⋅ I 3 Cátedra de Ingeniería Rural Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real Sustituyendo las variables por sus valores, se tiene: q = 2.5 t/m = 25 kg/cm L = 600 cm E = 2⋅106 kg/cm2 I= 1 1 ⋅ b ⋅ h3 = ⋅ b ⋅ 20 3 12 12 Así, despejando la anchura de la sección rectangular b, se obtiene: 12 ⋅ q ⋅ L4 b= 162 ⋅ E ⋅ h 3 y dando valores numéricos b= 12 ⋅ 25 ⋅ 600 4 = 15 cm 162 ⋅ 2 ⋅ 10 6 ⋅ 20 3 Por tanto, la sección rectangular buscada tiene de canto 20 cm y de anchura 15 cm. 4