Cátedra de Ingeniería Rural Calcular la viga continua de la figura

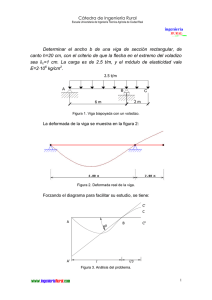
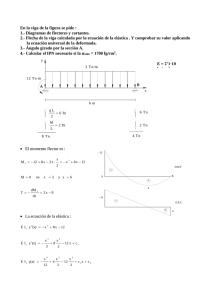
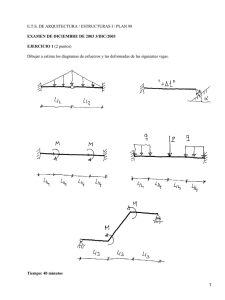
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
Calcular la viga continua de la figura sometida a una carga uniforme de
600 kp/m. Dimensionarla con un perfil IPN. Realizar también la comprobación a
flecha.
600 kp/m
A
B
6m
C
3m
Las leyes de esfuerzos cortantes y de momentos flectores se
representan en los diagramas siguientes. Las unidades que aparecen en ellos
son m y t.
1
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
Se puede comprobar que la sección más desfavorable es el apoyo B,
donde coinciden el cortante máximo con el momento flector máximo. Estas
solicitaciones son:
Q = 0.875 ⋅ q ⋅ l + 1.188 ⋅ q ⋅ l = 2.063 ⋅ 600 ⋅ 3 = 3713.4 kp
M = 0.375 ⋅ q ⋅ l2 = 0.375 ⋅ 600 ⋅ 32 = 2025 m ⋅ kp
Tanteando, sin tener en cuenta las tensiones cortantes:
M
≤ 1733 kp/cm 2
W
Por tanto, el módulo resistente de la viga ha de superar el valor:
W≥
M
202500
=
= 117 cm3
1733
1733
Elegimos un perfil IPN 200.
W x=214 cm3.
Aalma=159· 7.5=1192.5 mm2.
τ=
Q
3713.4
=
= 311.4 kp / cm2
A alma 11.925
σ=
M 202500
=
= 946.3 kp/cm 2
W
214
σco = σ2 + 3 ⋅ τ2 = 946.3 2 + 3 ⋅ 311.42 = 1089.2 kp/cm 2 < 1733
2
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
Comprobación a flecha
La viga continua original puede calcularse superponiendo dos estados
de carga. Se suprime el apoyo superabundante B, estudiándose la ecuación de
la elástica en el tramo AB, introduciendo la condición de que la deformación
suma de los dos estados de carga virtuales debe ser nula.
Los estados de carga son:
Las deformadas de estos estados de carga son:
3
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
Analíticamente:
y=
q⋅ x
6⋅x
⋅ x 3 − 2 ⋅ l ⋅ x 2 + l3 =
⋅ x 3 − 2 ⋅ 900 ⋅ x 2 + 9003 =
6
24 ⋅ E ⋅ I
24 ⋅ 2.1⋅ 10 ⋅ 2140
-11
4
5.56297 ⋅ 10 ⋅ x − 1.00133 ⋅ 10− 7 ⋅ x 3 + 4.05541⋅ x
(
)
(
)
P ⋅ l ⋅ b ⋅ x  b2 x 2  − 3713.4 ⋅ 900 ⋅ 300 ⋅ x  3002
x2 
=



y AC =
⋅ 1 −
−
⋅ 1− 2 − 2  =
2
2 
6 ⋅ E ⋅ I 
l
l 
6 ⋅ 2.1⋅ 106 ⋅ 2140
900
900


-2
3
−8
- 3.30521⋅ 10 ⋅ x + 4.59058 ⋅ 10 ⋅ x
Sumando ambas expresiones, se obtiene:
y = 5.56297 ⋅ 10 -11 ⋅ x 4 − 5.42277 ⋅ 10 −8 ⋅ x 3 + 7.50200 ⋅ 10−3 ⋅ x
Para determinar la posición del máximo en este tramo, se deriva e iguala
a cero, de modo que:
y' = 2.22519 ⋅ 10-10 ⋅ x 3 − 1.62683 ⋅ 10 −7 ⋅ x 2 + 7.50200 ⋅ 10−3 = 0
Resolviendo la ecuación, se determinan las raíces:
x1 = −191.2 cm
x 2 = 270.6 cm
x 3 = 651.7 cm
De ellas, únicamente la segunda tiene significado físico. Por tanto, la
flecha vale:
y = 5.56297 ⋅ 10 -11 ⋅ 270.6 4 − 5.42277 ⋅ 10 −8 ⋅ 270.63 + 7.50200 ⋅ 10−3 ⋅ 270.6 = 1.25 cm
La deformada de la viga se muestra en la imagen de la página siguiente,
en la que se muestran los valores de las deformaciones en cm.
4
Cátedra de Ingeniería Rural
Escuela Universitaria de Ingeniería Técnica Agrícola de Ciudad Real
Como no se dispone de ninguna restricción a la hora de determinar la
flecha máxima admisible, ya que no aparece en el enunciado, será el alumno
L
600
quien determine el límite. Así, para el menos exigente,
=
= 2.4 cm , la
250 250
viga dimensionada con un perfil IPN 200 es admisible. En cambio, si se adopta
L
600
=
= 1.2 cm , el perfil seleccionado no sería
el límite más exigente,
500 500
válido.
5