EJERCICIOS DE TRIGONOMETRÍA
Anuncio

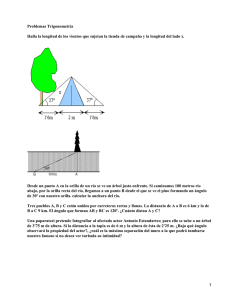
EJERCICIOS DE TRIGONOMETRÍA EJERCICIOS PROPUESTOS 1. El vigía de un barco pirata observa el punto más alto de un acantilado bajo un ángulo de 60º. Si el barco se aleja 100 m se observa bajo un ángulo de 45º. Calcula la altura del acantilado. Solución: 150 + 50 3 metros. 2. Resuelve el triángulo conociendo B̂ = 60º y el cateto b = 25 cm. Solución: Ĉ = 30º, la hipotenusa a = 50 3 25 3 cm y el otro cateto c = cm. 3 3 3. Calcula la longitud de los lados de un triángulo, sabiendo que su altura mide 10 m y que el ángulo desigual es de 120º. Solución: Los lados iguales miden 20 m, y el lado desigual, 20 3 m. 4. Calcula la altura de una torre, sabiendo que a 300 m de su pie se ve bajo un ángulo de 10º. Solución: h = 52,89 m. 5. Halla la altura de un edificio sabiendo que desde dos puntos alineados con la base y distantes entre sí 80 m, se ve bajo ángulos de 60º y 45º, respectivamente. ción: Solu- x = 197,37 m 6. Dos caminos rectos que se cortan forman un ángulo de 30º. En uno de ellos, a 1000 m del cruce, hay una gasolinera. Encontrar la menor distancia desde la estación de gasolina hasta el otro camino. 7. Una carretera asciende 3m por cada 100 m de recorrido. ¿Qué ángulo forma con la horizontal?. Solución: 1º 43’ 9’’. 8. Calcula la longitud de los lados de un triángulo isósceles, sabiendo que su altura mide 10 m y que el ángulo desigual es de 120º. Ejercicios de Trigonometría 4ºE.S.O. Página 1 EJERCICIOS RESUELTOS 1. De un triángulo rectángulo se conocen b= 20cm y c= 40 cm. Resolverlo. Las Incógnitas son: Bˆ , Cˆ y a C tgBˆ = a b (con una calculadora) b 20 Cˆ = 90º −26º 33′54′′ = 63º 26′6′′ ; senBˆ = = ⇒ a a 20 20 a= = =24,57 cm sen 26º33′54 ′′ 0,4472135 B A b 20 1 = = ⇒ Bˆ = 26º33′54′′ c 40 2 c 2. Resolver un triángulo rectángulo del que se conocen B=45º y c = 20 cm Solución: Bˆ + Cˆ = 90º ⇒ Cˆ = 45º c c 20 40 cos Bˆ = ⇒ a = = = = 20 2cm a cos Bˆ 2 2 2 b 2 senBˆ = ⇒ b = a ⋅ senBˆ = 20 2 ⋅ = 20cm a 2 3. Hallar la inclinación de la sombra proyectada por un edificio de 200 m de altura cuando la inclinación de los rayos del sol es de 30º. Como: C tg 30º = AB = 30º 200 AB 200 ⇒ AB = 346,41 m tg 30º 200 m B Ejercicios de Trigonometría 4ºE.S.O. Página 2 4. Desde un punto del suelo se ve el punto más alto de una torre formando ángulo de 30º con la horizontal. Si nos acercamos 10 m hacia su pie, éste ángulo es de 60º. Hallar la altura de la torre. h h 3= tg 60º = x x ⇔ tg 30º = h 3= h x + 10 3 x + 10 h Despejamos h de las dos ecuaciones 60º 0 x 30º e igualamos los resultados: 10 m h= h = 3⋅x 3⋅ x= nemos: 3 ⋅ ( x + 10) 3 3 ⋅ ( x + 10) podemos dividir los dos miembros de la ecuación por 3 x= 3 y te- x + 10 ⇔ 3x = x + 10 ⇔ 2 x = 10 ⇔ x = 5 Pero como nos piden la altura: 3 h = 3 ⋅ x = 3 ⋅ 5 ≅ 8,66 m 5. Un faro tiene una altura de 36 m sobre el nivel del mar. El ángulo de depresión de una embarcación es de 15º. Hallar a qué distancia está la embarcación del faro. FA RO tg15º = 15º 36 NE 36 m 15º NE = N Ejercicios de Trigonometría 36 = 134,35 m tg15º E 4ºE.S.O. Página 3 6. En el punto más alto de una pequeña elevación de terreno hay un poste de 3m de altura. Desde un punto A situado en el terreno llano se ve el pie B, del poste, bajo un ángulo de 38º 30’, y el C 3m B extremo superior c bajo un ángulo de 45º 15’. Hallar la altura del montículo: Los triángulos CPA y BPA son rectángulos x A P y En el primero: 3+ x = tg 45º15′ y ⇒ 3 + x = y ⋅ tg 45º15′ En el segundo: x = tg 38º 30′ ⇒ x = y ⋅ tg 38º 30′ . y donde: De 3 + x tg 45º15′ = = 1,2682 ⇒ x ≅ 11,2 m x tg 38º 30′ x = tg 38º 30′ ⇒ x = y ⋅ tg 38º 30′ y 7. Desde F, el punto más alto de un faro situado a 200 m sobre el nivel del mar, se divisa un barco B, con ángulo de depresión igual a 18º 45’. Cinco minutos más tarde la posición del barco es C y se divisa desde F bajo un ángulo de 15º 15’. Calcular la velocidad del barco sabiendo que la trayectoria CB es perpendicular a la PB, siendo P el pie del faro Los triángulos FPB y FPC son rectángulos en P y el PBC es rectángulo en B Ejercicios de Trigonometría 4ºE.S.O. Página 4 F 18º 45' 200 15º 15' C 90º 18º 45' 90º B P En el FPB: 200 200 = tg18º 45' ⇒ PB = = 589,2 m PB tg18º 45' En el FPC: 200 200 = tg15º15' ⇒ PC = = 733,6 m PC tg15º15' ByC están en el mismo plano, en el mar En el PBC: BC = PC 2 − PB 2 = 191.012,32 = 437,05 m El espacio recorrido es de 437,05 m en 5 minutos, luego la velocidad es v = 5,245 km/h SOLUCIONES A LOS EJERCICIOS PLANTEADOS EN EL MENÚ Resolución de triángulos: Cuando el ángulo es de 30º, la longitud de la sombra es aproximadamente de 38 m. Si el ángulo es de 40º, la longitud de la sombra es aproximadamente 26 m. Ejercicios de Trigonometría 4ºE.S.O. Página 5 Ejercicio de la buceadora: Aplicando la tangente del ángu100 m lo conocido a los dos triángulos rectángulos: x 100-x 35,0 ° 30,0 ° tg 30º = h x tg 35º = h 100 - x h Resolviendo el sistema por igualación, obtenemos que h = 31,64 m. Ejercicio avioneta: A h 30,0 ° 50,0 ° P2 P1 x 350 m Sean P1 y P2 los dos portaviones y A la avioneta. Aplicando tangentes en los dos triángulos rectángulos: tg 50º = h x h tg 30º = 350 + x Resolviendo el sistema, obtenemos que la altura a la que vuela la avioneta es aproximadamente h = 391,96 m. Ejercicios de Trigonometría 4ºE.S.O. Página 6 Ejercicio pagoda: h' h 45,0 ° x 30,0 ° 10 m 1,60 m 1,60 m 10 m La altura de la pagoda será h = h’ + 1,60 tg 45º = h′ x tg 30º = h′ Resolviendo el sistema, obtenemos h’ = 13, 67 m x + 10 Por lo tanto la pagoda mide aproximadamente h = 13,67 + 1,60= 15,27 m Ejercicios de Trigonometría 4ºE.S.O. Página 7