ÁNGULOS. A B O D C
Anuncio

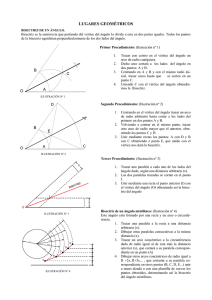
ÁNGULOS. ÁNGULO IGUAL A OTRO DADO. (Ilustración nº 1). A D B O O' C ILUSTRACIÓN Nº 1 Los ángulos se miden por su mayor o menor abertura y no por la longitud de sus lados, por ello para trazar un ángulo igual a otro, debemos proceder de la siguiente manera: 1. Centrando en el vértice del ángulo dado, trazamos un arco de radio cualquiera que cortará a los lados de dicho ángulo en los puntos A y B. 2. Con el mismo radio trazar otro arco sobre otra semirrecta centrando en uno de sus extremos obteniendo el punto C donde el arco la corte. 3. Centrando en C transportar sobre el arco anterior la magnitud AB, obteniendo el punto D que unido al origen de la semirrecta nos dará un ángulo igual al primero dado. SUMA DE ÁNGULOS. (Ilustración nº 2). A B A+B A B Se trata de construir dos ángulos consecutivos e iguales a los dados. Para resolver este problema utilizaremos el método anteriormente explicado: 1. Trazamos primero uno de los dos ángulos dado (procedimiento anterior). 2. Sumamos al otro ángulo por el mismo método de manera que el ángulo resultante (suma de los dos) tendrá un extremo del primero y otro del segundo ángulo. ILUSTRACIÓN Nº 2 A RESTA DE ÁNGULOS. (Ilustración nº 3). A-B A El procedimiento es parecido al anterior varía en que al transportar uno de los ángulos no se hace a continuación, sino sobre el otro; el espacio que quede sin cubrir será el resultado de la recta B B ILUSTRACIÓN Nº 3 B DIVISIÓN DE UN ÁNGULO RECTO EN TRES PARTES IGUALES. D (Ilustración nº 4). 1. Con centro en el vértice del ángulo (O) y con radio cualquiera trazamos un arco que corte a los lados del ángulo en A y B. C 2. Con el mismo radio y centrando en A y B trazamos dos arcos que corten al anterior en los puntos C y D. 3. Uniendo C y D con O tendremos divido el ángulo. A O ILUSTRACIÓN Nº 4