LUGARES GEOMÉTRICOS

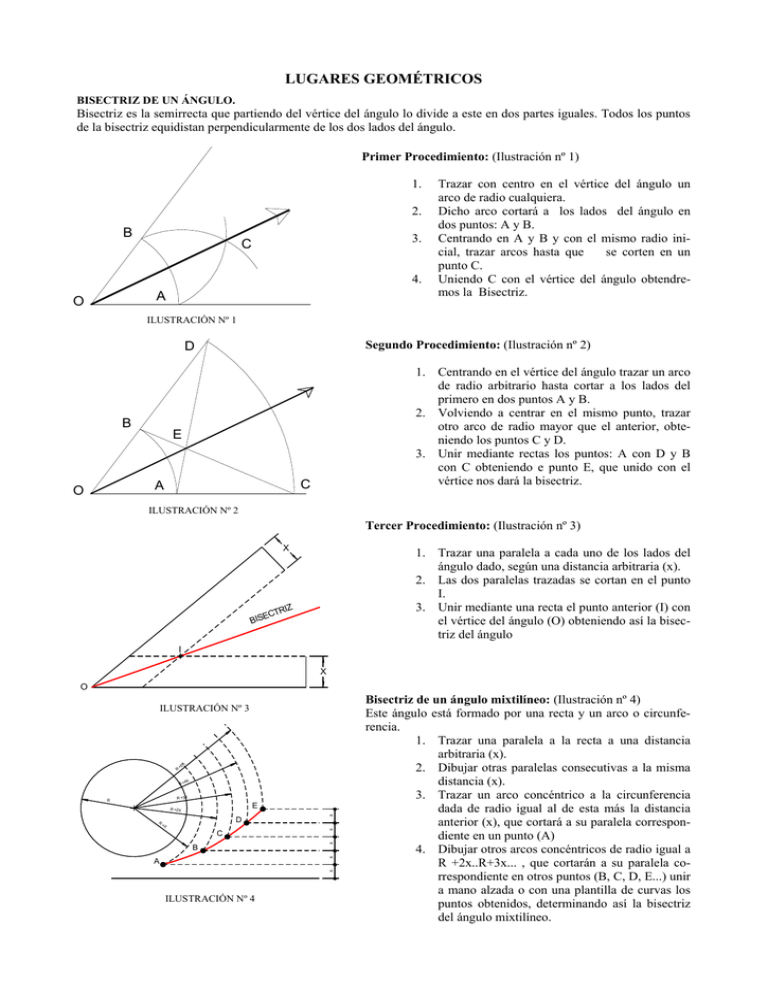
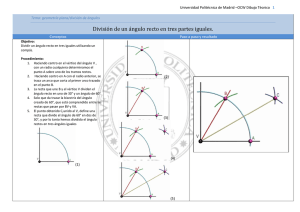
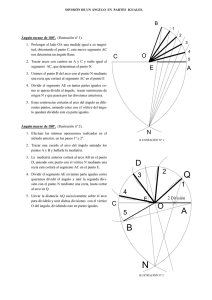
LUGARES GEOMÉTRICOS
BISECTRIZ DE UN ÁNGULO.
Bisectriz es la semirrecta que partiendo del vértice del ángulo lo divide a este en dos partes iguales. Todos los puntos
de la bisectriz equidistan perpendicularmente de los dos lados del ángulo.
Primer Procedimiento: (Ilustración nº 1)
1.
2.
B
3.
C
4.
A
O
Trazar con centro en el vértice del ángulo un
arco de radio cualquiera.
Dicho arco cortará a los lados del ángulo en
dos puntos: A y B.
Centrando en A y B y con el mismo radio inicial, trazar arcos hasta que
se corten en un
punto C.
Uniendo C con el vértice del ángulo obtendremos la Bisectriz.
ILUSTRACIÓN Nº 1
Segundo Procedimiento: (Ilustración nº 2)
D
B
E
C
A
O
1. Centrando en el vértice del ángulo trazar un arco
de radio arbitrario hasta cortar a los lados del
primero en dos puntos A y B.
2. Volviendo a centrar en el mismo punto, trazar
otro arco de radio mayor que el anterior, obteniendo los puntos C y D.
3. Unir mediante rectas los puntos: A con D y B
con C obteniendo e punto E, que unido con el
vértice nos dará la bisectriz.
ILUSTRACIÓN Nº 2
Tercer Procedimiento: (Ilustración nº 3)
X
1. Trazar una paralela a cada uno de los lados del
ángulo dado, según una distancia arbitraria (x).
2. Las dos paralelas trazadas se cortan en el punto
I.
3. Unir mediante una recta el punto anterior (I) con
el vértice del ángulo (O) obteniendo así la bisectriz del ángulo
RIZ
ECT
BIS
I
X
O
ILUSTRACIÓN Nº 3
R
X
+5
4X
R+
R +3X
D
+X
C
X
B
X
R
X
E
R +2X
X
R
X
A
ILUSTRACIÓN Nº 4
Bisectriz de un ángulo mixtilíneo: (Ilustración nº 4)
Este ángulo está formado por una recta y un arco o circunferencia.
1. Trazar una paralela a la recta a una distancia
arbitraria (x).
2. Dibujar otras paralelas consecutivas a la misma
distancia (x).
3. Trazar un arco concéntrico a la circunferencia
dada de radio igual al de esta más la distancia
anterior (x), que cortará a su paralela correspondiente en un punto (A)
4. Dibujar otros arcos concéntricos de radio igual a
R +2x..R+3x... , que cortarán a su paralela correspondiente en otros puntos (B, C, D, E...) unir
a mano alzada o con una plantilla de curvas los
puntos obtenidos, determinando así la bisectriz
del ángulo mixtilíneo.