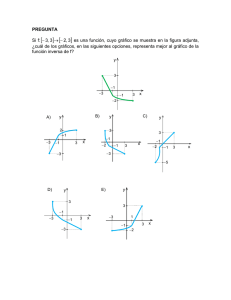
Guía n°3: Función Inversa
Anuncio
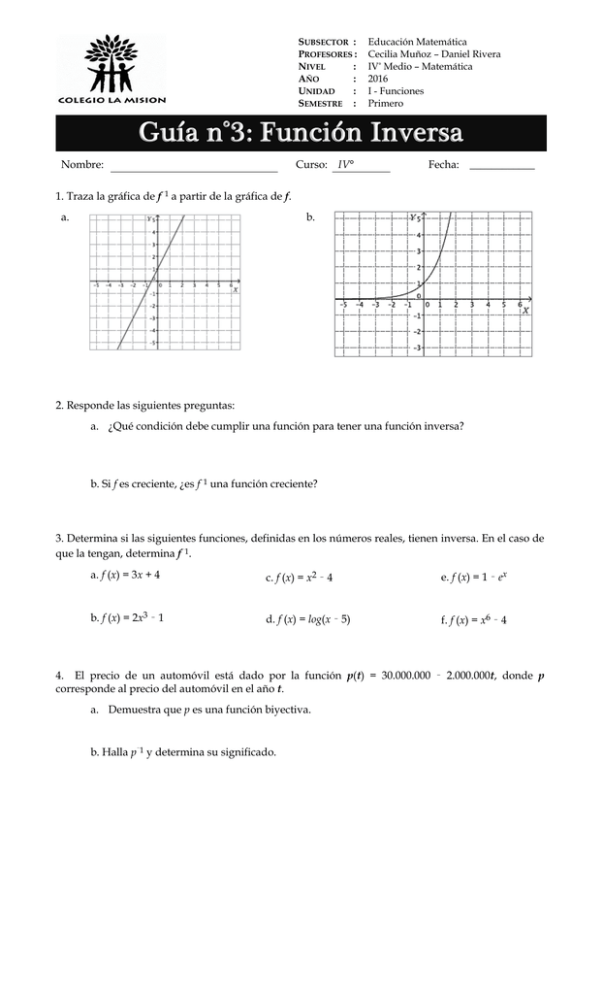
SUBSECTOR : PROFESORES : NIVEL : AÑO : UNIDAD : SEMESTRE : Educación Matemática Cecilia Muñoz – Daniel Rivera IV° Medio – Matemática 2016 I - Funciones Primero Guía n°3: Función Inversa Curso: IV° Nombre: Fecha: ____________ 1. Traza la gráfica de f–1 a partir de la gráfica de f. a. b. 2. Responde las siguientes preguntas: a. ¿Qué condición debe cumplir una función para tener una función inversa? b. Si f es creciente, ¿es f–1 una función creciente? 3. Determina si las siguientes funciones, definidas en los números reales, tienen inversa. En el caso de que la tengan, determina f–1. a. f (x) = 3x + 4 c. f (x) = x2 – 4 e. f (x) = 1 – ex b. f (x) = 2x3 – 1 d. f (x) = log(x – 5) f. f (x) = x6 – 4 4. El precio de un automóvil está dado por la función p(t) = 30.000.000 – 2.000.000t, donde p corresponde al precio del automóvil en el año t. a. Demuestra que p es una función biyectiva. b. Halla p–1 y determina su significado. Cuarto año Medio 2016 – Educación Matemática Profesores Cecilia Muñoz – Daniel Rivera 5. Al colocar un objeto en el platillo de una balanza analógica, el puntero describe un arco de medida, en grados, directamente proporcional a la masa del cuerpo. Para 1 kg el puntero describe un arco de 36°. a. Escribe una función que exprese el desplazamiento del puntero en función de la masa corporal x de un objeto, con x < 10. b. Escribe una función que exprese la masa, en kilogramos, de un objeto colocado en la balanza, en función del desplazamiento x del puntero, con x < 360°. c. ¿Cuál es la relación entre las funciones obtenidas en los puntos anteriores? 6. La ley de enfriamiento de Newton permite determinar el momento de la muerte de una persona con la función T(t) = T0 + (T1 – T0)(0,97)t, donde T es la temperatura del individuo t horas después de su muerte. T0 es la temperatura ambiente y T1 la temperatura en el momento de su muerte. a. Halla T–1 y explica su significado. b. Si T0 = 25 oC, T1 = 37 oC y T = 31 oC, ¿cuánto tiempo ha pasado desde que murió la persona? 7. Argumenta por qué una función que tiene inversa debe ser biyectiva. 8. Explica como verificas que una función es la inversa de otra. Página - 2 - Cuarto año Medio 2016 – Educación Matemática Profesores Cecilia Muñoz – Daniel Rivera SOLUCIONARIO 1. a. b. 2. a. La función debe ser biyectiva. b. Si. 3. a. Si tiene inversa, f –1(x) = 𝑥–4 3 3 𝑥+1 b. Si tiene inversa, f (x) = √ –1 2 c. No tiene inversa. d. Si tiene inversa, f –1(x) = 10x + 5 e. Si tiene inversa, f –1(x) = ln(1 – x) f. No tiene inversa. 4. a. p es inyectiva, ya que: p(t1) = p(t2) 30000000 – 2000000t1 = 30000000 – 2000000t2 – 2000000t1 = – 2000000t2 t1 = t2 p es sobreyectiva, porque es una función lineal, luego, p es biyectiva. 30.000.000 – 𝑡 –1 b. p (t) = 2.000.000 Se puede interpretar como estimar los años de un automóvil, si se conoce su precio. 5. a. f(x) = 36x 𝑥 b. g(x) = 36 c. f y g son funciones inversas. 6. a. T –1(t) = 1 𝑙𝑛 0,97 ・ ln ( 𝑦 – 𝑇0 ) 𝑇1 – 𝑇0 b. 22 horas y 45 minutos, aproximadamente. 7. Debe ser inyectiva para que a cada elemento del dominio de f –1 (recorrido de f ) le corresponda una única imagen (preimagen de los elementos del recorrido de f ) y debe ser sobreyectiva para que exista la función f –1 para todo elemento del dominio de f –1 (recorrido de f ) . 8. Verificando que f(f –1(x)) = x. Página - 3 -