Calcula la potencia e intensidad de cortocircuito en los bornes del
Anuncio

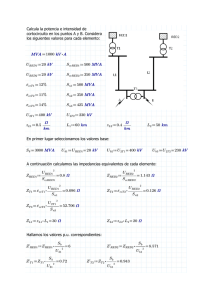
Calcula la potencia e intensidad de cortocircuito en los bornes del primario y del secundario del transformador 4. Considera los siguientes valores para cada elemento: ≔ 1000 ⋅ URED ≔ 132 SccRED ≔ 1500 εccT1 ≔ 12% Sn1 ≔ 20 εccT2a5 ≔ 4% Sn2a5 ≔ 6 U2T1 ≔ 20 U2T2a5 ≔ 6 zL1 ≔ 0.07 ―― L1 ≔ 3 zL2a6 ≔ 0.12 ―― L2 ≔ 900 L3 ≔ 700 L4 ≔ 500 L5 ≔ 800 L6 ≔ 900 En primer lugar seleccionamos los valores base: Sb ≔ 6 Ub1 ≔ URED = 132 Ub2 ≔ U2T1 = 20 A continuación calculamos las impedancias equivalentes de cada elemento: URED 2 ZRED1 ≔ ――― = 11.616 SccRED URED 2 ZT1 ≔ εccT1 ⋅ ――― = 104.544 Sn1 U2T1 2 ZT4 ≔ εccT2a5 ⋅ ―― = 2.667 Sn2a5 ZL1 ≔ zL1 ⋅ L1 = 0.21 ZL2 ≔ zL2a6 ⋅ L2 = 0.108 ZL3 ≔ zL2a6 ⋅ L3 = 0.084 ZL4 ≔ zL2a6 ⋅ L4 = 0.06 ZL5 ≔ zL2a6 ⋅ L5 = 0.096 ZL6 ≔ zL2a6 ⋅ L6 = 0.108 Hallamos los valores p.u. correspondientes: Sb = 0.004 Z'RED1 ≔ ZRED1 ⋅ ―― Ub1 2 Sb Z'T1 ≔ ZT1 ⋅ ―― = 0.036 Ub1 2 Sb Z'T4 ≔ ZT4 ⋅ ―― = 0.04 Ub2 2 Sb Z'L1 ≔ ZL1 ⋅ ―― = 7.231 ⋅ 10 −5 2 Ub1 Sb Z'L4 ≔ ZL4 ⋅ ―― = 9 ⋅ 10 −4 2 Ub2 Sb Z'L2 ≔ ZL2 ⋅ ―― = 0.002 Ub2 2 Sb Z'L5 ≔ ZL5 ⋅ ―― = 0.001 Ub2 2 Sb Z'L3 ≔ ZL3 ⋅ ―― = 0.001 Ub2 2 Sb Z'L6 ≔ ZL6 ⋅ ―― = 0.002 Ub2 2 Cortocircuito en el primario del T4 1 Z'eq ≔ Z'RED1 + Z'L1 + Z'T1 + ―――――――――― = 0.042 1 1 + ―――――― ―――― Sb Z'L6 + Z'L5 Z'L2 + Z'L3 + Z'L4 = 143.667 Scc ≔ ―― Z'eq Scc = 4.147 Icc ≔ ―――― ‾‾ 3 ⋅ U2T1 Cortocircuito en el secundario del T4 1 Z'eq ≔ Z'RED1 + Z'L1 + Z'T1 + ―――――――――― + Z'T4 = 0.082 1 1 + ―――――― ―――― Sb Z'L6 + Z'L5 Z'L2 + Z'L3 + Z'L4 = 73.382 Scc ≔ ―― Z'eq Scc Icc ≔ ―――― = 2.118 ‾‾ 3 ⋅ U2T1