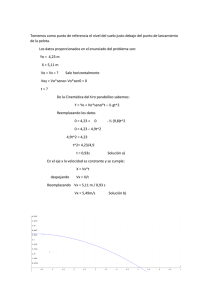
Solución al examen del tema 2

Cuestiones
1. Una bola pequeña rueda en el interior de un recipiente cónico de eje vertical
y semiángulo α en el vértice ¿A qué altura h sobre el vértice se encontrará la
bolita en órbita estable con una velocidad de v?
La situación es el que se muestra en la figura 1. Sobre la bola las únicas fuerzas que actúan son el peso, en
N
dirección vertical y hacia abajo, y la normal que realiza
R
la superficie del cono sobre la bola, perpendicular a la
superficie del cono y formando un ángulo α con el plano
P
horizontal.
v
Se toma el eje x en la dirección horizontal hacia el
α h
centro de curvatura (plano horizontal), y el eje y en
α
h
la dirección vertical (figura 1b). La bola da vueltas a
y
una altura h respecto del vértice del cono, estacionaria,
por lo que ni sube ni baja, y la aceleración en el eje
x
y es igual a cero. Por otro lado, en el plano horizontal está describiendo una circunferencia con velocidad
(a)
(b)
v constante, por lo que la bola posee una aceleración
Figura 1: Cuestión 1
normal hacia el centro de curvatura.
Teniendo en cuenta las anteriores fuerzas, la segunda ley de Newton queda:
2
dirección x −→ N cos α = m vR
~
~
~
ΣF = P + N = m~a ⇒
dirección y −→ N senα − mg = 0
De la segunda ecuación se obtiene el valor del módulo de la normal, que resulta:
N=
mg
senα
Por otro lado, el radio de curvatura de la circunferencia que describe la bola depende de la
altura a la que gira, tal que
tan α =
R
por lo que R = h tan α
h
Sustituyendo las anteriores dos expresión de R y N en el equilibrio de fuerzas en la dirección
x resulta:
v2
cos α
mg
=m
senα
h tan α
y simplificando se obtiene la expresión que se pide de la altura en función de la velocidad
v2
h=
g
2. Una bola de billar choca con otra que inicialmente está en reposo. Determı́nese la relación que deben cumplir las masas de ambas bolas para que la
primera quede en reposo después del choque, en el caso de que el choque sea
elástico y en el caso de que sea inelástico.
Tanto si es elástico como si no, la interacción entre las dos bolas de billar es un choque
instantáneo, en el que no existe ninguna fuerza impulsiva en la dirección horizontal, por lo
1
que el momento lineal total del sistema en esta dirección se conserva. Si se supone el choque
unidimensional, p10 y p20 son el momento de la bola uno y la dos antes del choque, y p1f y p2f
son el momento de la bola uno y la dos después del choque, la conservación del momento lineal
queda:
p10 + p20 = p1f + p2f
Inicialmente, la bola 2 se encuentra en reposo, por lo que p20 = 0; mientras que tras el
choque es la bola 1 la que queda en reposo, es decir p1f = 0. Si se tiene en cuenta estas dos
condiciones, la definición del momento lineal (~p = m~v ) y se nota con m1 y m2 las masas de la
bola uno y la bola dos, la anterior ecuación de conservación resulta:
m1 v10 = m2 v2f
(1)
Esta ecuación se cumplirá tanto en el caso de choque elástico como inelástico. Vamos a estudiar
estos dos casos por separado.
Choque elástico En este caso, se tiene que la energı́a antes y después del choque es la misma.
Las energı́as antes (Eo ) y después del choque (Ef ) son:
1
1
2
2
y Ef = m2 v2f
Eo = m1 v1o
2
2
La igualdad de estas dos energı́as produce
1
1
2
2
2
2
m1 v10
= m2 v2f
=⇒ m1 v10
= m2 v2f
= (m2 v2f )v2f
2
2
Pero también debe cumplirse la ecuación (1), que sustituyendo en la anterior ecuación
produce:
2
m1 v10
= (m1 v10 )v2f =⇒ v10 = v2f
Si esto se sustituye en la ecuación (1), resulta:
m1 = m2
Choque inelástico En este caso se pierde energı́a en el choque, por lo que se cumple:
1 2
1 2
2
2
Eo > Ef =⇒ mv1o
> mv2f
=⇒ m1 v1o
> m2 v2f
= (m2 v2f )v2f
2
2
Al igual que en el anterior caso, también debe cumplirse la ecuación (1), que sustituyéndola
en la anterior ecuación produce:
2
m1 v10
> (m1 v10 )v2f =⇒ v1o > v2f
Si esto se substituye en la ecuación (1) resulta:
m1 < m2
2
Problemas
1. El parabrisas de un coche forma un ángulo de 60o con la horizontal. Cuando el coche acelera uniformemente, se coloca suavemente un paquete sobre él de
2 kg. Calcular el rango de aceleraciones que puede llevar el coche para que el paquete permanezca en reposo respecto del parabrisas si el coeficiente de rozamiento
estático entre el parabrisas y el paquete es de 0.3.
Cuando la aceleración del coche sea muy grande, el paquete se desplazará hacia arriba del
parabrisas, a lo que se opondrá una fuerza de rozamiento hacia abajo. Sin embargo, cuando la
aceleración sea muy pequeña, el paquete tenderá a desplazarse hacia abajo del parabrisas, a lo
que se opondrá una fuerza de rozamiento hacia arriba.
Por tanto, existen dos situaciones lı́mite: una en la que está apunto de irse hacia arriba
(figura 2(a)), y otra la que está a punto de irse hacia abajo (figura 2(b)).
a
a
y
N
60º
P
Fr
Fr
y
x
60º
(a)
N
x
P
(b)
Figura 2: Problema 1
Hagamos primero el caso en el que está a punto de irse hacia arriba. En este caso, si se
aplica la segunda ley de Newton, teniendo en cuenta la geometrı́a presente en la figura 2(a) se
tiene:
~ + F~r = m~a ⇒ dirección y −→ N cos α − mg − Fr senα = 0
ΣF~ = P~ + N
dirección x −→ N senα + Fr cos α = ma
donde α = 60o .
Como ésta es una situación lı́mite Fr = µe N , con lo que las anteriores ecuaciones quedan:
N cos α − mg − N µe senα = 0
N senα + N µe cos α = ma
De la primera resulta el módulo de la normal:
N=
mg
cos α − µe senα
Sustituyendo este valor en la segunda se llega a la expresión de la aceleración:
a=g
senα + µe cos α
= 41,45 m/s2
cos α − µe senα
Cualquier aceleración mayor que ésta hará que el paquete se desplace hacia arriba del parabrisas.
El caso en el que la aceleración es tan pequeña que está apunto de desplazarse hacia abajo
del parabrisas está esquematizado en la figura 2(b). En este caso la segunda ley de Newton
quedarı́a:
~ + F~r = m~a ⇒ dirección y −→ N cos α − mg + Fr senα = 0
ΣF~ = P~ + N
dirección x −→ N senα − Fr cos α = ma
3
Al igual que antes, ésta es una situación lı́mite, por lo que Fr = µe N y las anteriores ecuaciones
quedan:
N cos α − mg + N µe senα = 0
N senα − N µe cos α = ma
De la primera resulta el módulo de la normal:
N=
mg
cos α + µe senα
Sustituyendo este valor en la segunda se llega a la expresión de la aceleración:
a=g
senα − µe cos α
= 9,23 m/s2
cos α + µe senα
Cualquier aceleración menor que ésta hará que el paquete se desplace hacia abajo del parabrisas.
Por tanto, los valores de la aceleración para los cuales el paquete no desliza en el parabrisas
son:
9,23 m/s2 ≤ a ≤ 41,45 m/s2
2. Una bala de 7 g es disparada con un arma de fuego contra un bloque de
madera de masa 1 kg apoyado sobre el suelo y en contacto con una pared vertical;
la bala penetra en el bloque de madera hasta una profundidad de 8 cm. Ahora
se coloca el bloque de madera sobre una superficie horizontal sin rozamiento y
se dispara con el arma otra bala de 7 g contra el bloque. Suponiendo que las
velocidades de disparo son idénticas en ambos casos, ¿qué distancia penetrará la
bala en el bloque?
En el primer caso, toda la energı́a que inicialmente tenı́a la bala se ha perdido, ya que
después del choque el bloque y la bala quedan en reposo. Esta energı́a perdida se ha empleado
en penetrar en el bloque, con la consiguiente deformación. La energı́a perdida es:
1
∆E1 = mv02
2
donde m es la masa de la bala y v0 la velocidad que lleva antes del choque.
En el segundo caso, la bala se incrusta también en el bloque, pero después del choque
la bala y el bloque se mueven con una cierta velocidad. Esta velocidad final (vf ) se puede
calcular teniendo en cuenta que en este segundo caso no existe ninguna fuerza exterior impulsiva
actuando sobre el sistema bala-bloque en el dirección horizontal, por lo que el momento lineal
total del sistema se conservará en esta dirección:
ptotal
= ptotal
0x
fx
El momento lineal total inicial es ptotal
= mv0 , mientras que el momento lineal total final es
0x
ptotal
=
(m
+
M
)v
,
con
M
la
masa
del
bloque. Con esto, la conservación del momento lineal
f
fx
queda:
mv0 = (m + M )vf
lo que permite establecer una relación entre la velocidad después del choque y antes del choque:
m
vf = v0
m+M
Con esta velocidad final se puede calcular la energı́a perdida en el choque:
2
1 2 1
1 2 1
m
2
∆E2 = mv0 − (m + M )vf = mv0 − (m + M ) v0
2
2
2
2
m+M
4
1 mM 2
v
2m+M 0
La energı́a que se pierde en el choque es debida a la acción de las fuerzas de rozamiento
internas (Fr ), que son no-conservativas. Si se consideran estas fuerzas constantes durante el
tiempo que tarda la bala en incrustarse, el trabajo realizado por estas fuerzas será igual al valor
de la fuerza por la profundidad a la que se ha incrustado la bala. La energı́a perdida será por
tanto igual al trabajo de estas fuerzas de rozamiento, y por tanto, proporcional a la profundidad
a la que se ha incrustado la bala:
∆E1 = Fr d1
∆E2 = Fr d2
∆E2 =
donde d1 es la profundidad a la que se incrusta la bala en el primer caso y d2 la profundidad a
la que se incrusta la bala en el segundo caso. Dividiendo las energı́a se obtiene:
d1
∆E1
=
∆E2
d2
por lo que la profundidad a la que se incrusta la bala en el segundo caso es:
d2 = d1
∆E2
M
= d1
∆E1
M +m
d2 = 7,93 cm
3. Un hombre se encuentra sobre una barca de 200 kg en un lago. El hombre
se pone de pie y lanza una lata llena (masa 0,4 kg) con un ángulo de 45o , de
forma que llega justo hasta la orilla. Observa que la barca y él han retrocedido
1,2 m durante el tiempo que la lata ha estado en el aire. Sabiendo que el hombre
pesa 70 kg, calcúlese la distancia a la que se encuentra inicialmente de la orilla
y la velocidad con la que la lata fue lanzada.
Sobre el sistema barca-hombre-lata las únicas fuerzas que actúan son verticales, concretamente el empuje del agua sobre la barca y el peso, por lo que en la dirección horizontal el
momento total del sistema se conservará, durante todo el movimiento.
Por tanto, el momento total del sistema en la dirección horizontal antes (ptotal
0x ) y después
total
(pf x ) de haber lanzado la lata será el mismo (también lo será en la dirección vertical, pero
no resulta de utilidad en la resolución del problema). Como inicialmente está en reposo, esto
significa:
ptotal
= ptotal
0x
fx = 0
El momento total en la dirección horizontal después del lanzamiento será la suma del momento lineal de la lata, plx = ml vlx , en esa dirección más el momento lineal de la barca y el
hombre, pbhx = (mb + mh )vbhx ; con ml , mb y mh las masas de la lata, la barca y el hombre,
respectivamente, y vl y vbh los módulos de las velocidades de la lata y del sistema hombre-barca,
respectivamente. Como ya se ha dicho antes, la suma de los dos momentos tiene que ser nula:
pf x = plx + pbhx = ml vlx + (mb + mh )vbhx = 0
por lo que:
−ml
vlx
mb + mh
La lata se lanza con una velocidad vl y con un ángulo con la horizontal de α = 45o , por lo
que la velocidad horizontal de la barca y el hombre queda:
vbhx =
vbhx =
−ml
vl cos α = 0
mb + mh
5
Por otro lado, durante el tiempo que la lata está en el aire, la barca y el hombre retroceden
una distancia d1 = 1,2 m, de lo que se deduce que el tiempo que la lata ha estado en el aire t1
es:
d1 (mb + mh )
d1
=
t1 =
|vbhx |
ml vl cos α
El movimiento de la lata es una tiro parabólico, de forma que sus ecuaciones del movimiento
y la velocidad son:
1 2
x = x0 + v0x t
~r = ~r0 + ~v0 t + ~g t −→
y = y0 + v0y t − 12 gt2
2
vx = v0x
~v = ~v0 t + ~g t2 −→
vy = v0y − gt
Colocamos el origen de coordenadas en el punto en el que se lanza la lata, y suponemos
que la altura a la que se realiza el lanzamiento es la misma que la de la orilla, con lo que las
condiciones iniciales serán:
x0 = y0 = 0; v0x = vl cos α; v0y = vl senα
El punto en el que cae corresponde a y = 0, y el tiempo empleado en llegar a ese punto
corresponde al tiempo t1 , que ha aparecido con anterioridad. De esta forma:
1
1
1 2
0 = vl senαt1 − gt1 =⇒ 0 = t1 vl senα − gt1 =⇒ 0 = vl senα − gt1
2
2
2
Si se sustituye la expresión ya obtenida de t1 en la anterior ecuación, se obtiene una ecuación
donde la única incógnita es la velocidad de salida de la lata:
s
1 d1 (mb + mh )
gd1 (mb + mh )
0 = vl senα − g
⇒ vl =
2 ml vl cos α
2ml cos αsenα
vl = 89,1 m/s2
Para calcular la distancia a la que se encuentra la barca de la orilla inicialmente, d2 , sólo
hay que calcular la distancia horizontal recorrida por la lata:
d2 = vl cos αt1 = vl cos α
d1 (mb + mh )
d1 (mb + mh )
=
ml vl cos α
ml
d2 = 810 m
6