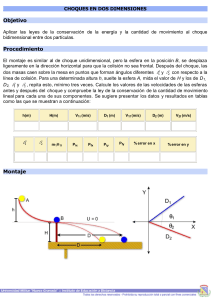
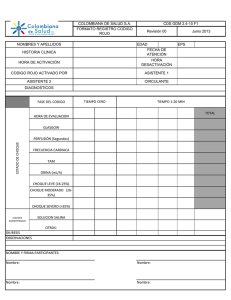
Como ω = rad 18 s ,el periodo es 1.

1.- Movimiento de la masa antes de que se rompa el muelle.
Es un movimiento armónico de amplitud
L
k
y pulsación ω=
.
4
m
Teniendo en cuenta las condiciones iniciales y en los ejes de la figura, la
ecuación queda:
x=
L
2
⎛
⎛ k
⎞⎞
1
1
t + π ⎟⎟ ⎟ → x = 1 + cos (18 t + π ) ( m )
⎜ 1 + cos ⎜⎜
⎜
⎟
2
2
⎝ m
⎠⎠
⎝
2.- Velocidad y aceleración de m en t1.
Basta con derivar dos veces la x(t) y sustituir el tiempo por su valor en t1.
x ( t1 ) =
L
= 1m
2
L k
m
=9
4 m
s
= 0 (x1 es el centro del m.a.s.)
v ( t1 ) =
a ( t1 )
3.-
Como ω = 18
rad
π
9
1
,el periodo es T = → t1 = T → 2 periodos y de periodo
s
9
4
4
4.- Por energías, como no hay variación de energía potencial, toda la energía
cinética se invierte en trabajo de la fuerza de rozamiento si queremos que la
masa se pare.
µ<
v12
→ µ < 4,05
gL
5.- Primero se resuelve el choque:
Conservación de la cantidad de movimiento: m v1 = m v1' +
Choque elástico: 1 = −
Es decir, v '2 =
m '
v2
2
v1' − v '2
v1 − v 2
4
m
v1 = 12 , y ésta es la velocidad inicial de un tiro horizontal.
3
s
Planteando las ecuaciones se obtiene que la coordenada x del punto del suelo
donde cae la masa m/2 es x3 = 6,8m