ANÁLISIS DE CORRIENTE DE MALLA (MÉTODO CONVENCIONAL)
Anuncio

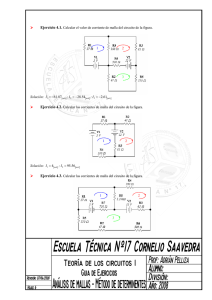
ANÁLISIS DE CORRIENTE DE MALLA (MÉTODO CONVENCIONAL) 1. Identificar mallas y súper mallas. 2. Asignar variables de corriente a cada malla independiente. 3. Escribir las ecuaciones de KVL para cada malla con el siguiente formato: (El voltaje de cada elemento en el circuito es igual al producto de la resistencia por la suma algebraica de las corrientes de malla que fluyen en el elemento. A11 I1 A12 I 2 ...A1n I n V An1 I1 An 2 I 2 ...Ann I n V 4. Si el circuito tiene fuentes dependientes, expresar la variable controladora en términos de la corriente de malla definida, sustituye esté en las ecuaciones de KVL. 5. Resuelve las ecuaciones resultantes. ANÁLISIS DE CORRIENTE DE MALLA (MÉTODO POR INSPECCIÓN) 1. Identificar mallas y súper mallas. 2. Asignar variables de corriente a cada malla independiente. 3. Construye el siguiente sistema de ecuaciones A C D B I1 I2 E F A = de las resistencias en la malla 1. B = de las resistencias en la malla 2. C = D = de las resistencias que tengan en comunes ambas mallas. Este valor es negativo si ambas corrientes de malla van en sentido opuesto, positivo si van en la misma dirección. 4. Si el circuito tiene fuentes dependientes, expresa la variable controladora en términos de las corrientes de malla que se definieron. 5. Para calcular las constantes E y F asume que las corrientes de malla son iguales a cero. I1=I2=0. 6. Para calcular E y F, hacer KVL en la malla correspondiente. Recuerda que las corrientes de mallas son iguales a cero. 7. Si el circuito tiene fuentes dependientes las constantes E y F van a tener variables. Para eliminar estas variables tienes que despejar estas variables dentro de la matriz de luego sustituir la variable controladora determinada en el paso 4. 8. Este método se puede expandir para sistemas de dos o más variables. Ver ejemplos en clase. By: Prof. Rubén Flores Flores ANÁLISIS DE VOLTAJE DE NODO (MÉTODO CONVENCIONAL) 1. Identificar nodos y súper nodos. 2. Asignar nodo de referencia. 3. Asignar variables de voltaje a cada nodo con respecto al de referencia (punto de menor potencial). 4. Asignar polaridad a cada elemento del circuito. 5. Asigna dirección positiva de la corriente (+ los que entran o + los que salen). 6. Escribe las ecuaciones de KCL a cada nodo (excepto el de referencia) midiendo el voltaje de cada elemento en termino de las variables definidas y luego aplica ley de ohm para determinar la corriente que entra o sale del nodo. 7. Si el circuito tiene fuentes dependientes, expresa la variable controladora en términos de las variables definidas y sustitúyelo en la ecuación. 8. Simplifica las ecuaciones resultantes. 9. Resuelve el sistema de ecuaciones para obtener los voltajes de cada nodo. ANÁLISIS DE VOLTAJE DE NODO (MÉTODO POR INSPECCIÓN) 1. Identificar nodos y súper nodos. 2. Asignar nodo de referencia. 3. Asignar variables de voltaje a cada nodo con respecto al de referencia (punto de menor potencial). 4. Asignar polaridad a cada elemento del circuito. 5. Asignar dirección positiva de la corriente que entran al nodo. 6. Construye el siguiente sistema de ecuaciones en forma de matriz. A D B C V1 V2 E F A = de los inversos de las resistencias conectadas al nodo 1. C = de los inversos de las resistencias conectadas al nodo 2. B = D = de los inversos de las resistencias que estén conectadas entre el nodo 1 y 2. 7. Si el circuito tiene fuentes dependientes, expresa la variable controladora en términos de las variables de voltaje definidos. 8. Para determinar las corrientes E y F asume que el voltaje V1 = V2 = 0. 9. Para calcular E, determina las corrientes que entran al nodo1. Mide los voltajes de cada elemento que este conectado al nodo y aplica ley de ohm. Recuerda que tienes que asumir que los voltajes V1 = V2 = 0. 10. Repite el paso 9 para cada nodo restante. 11. Si el circuito tenia fuentes dependientes las constantes E y F van a tener variables. Para eliminar estas variables tienes que despejar estas variables a dentro de la matriz. 12. Este método se puede expandir para sistemas de tres o más variables. Ver ejemplos de la clase de cómo expandir la matriz. By: Prof. Rubén Flores Flores