V Vx II = = 0 0 0 V kI IR VIR kI VIR kI VVV = - = - + - = - +
Anuncio
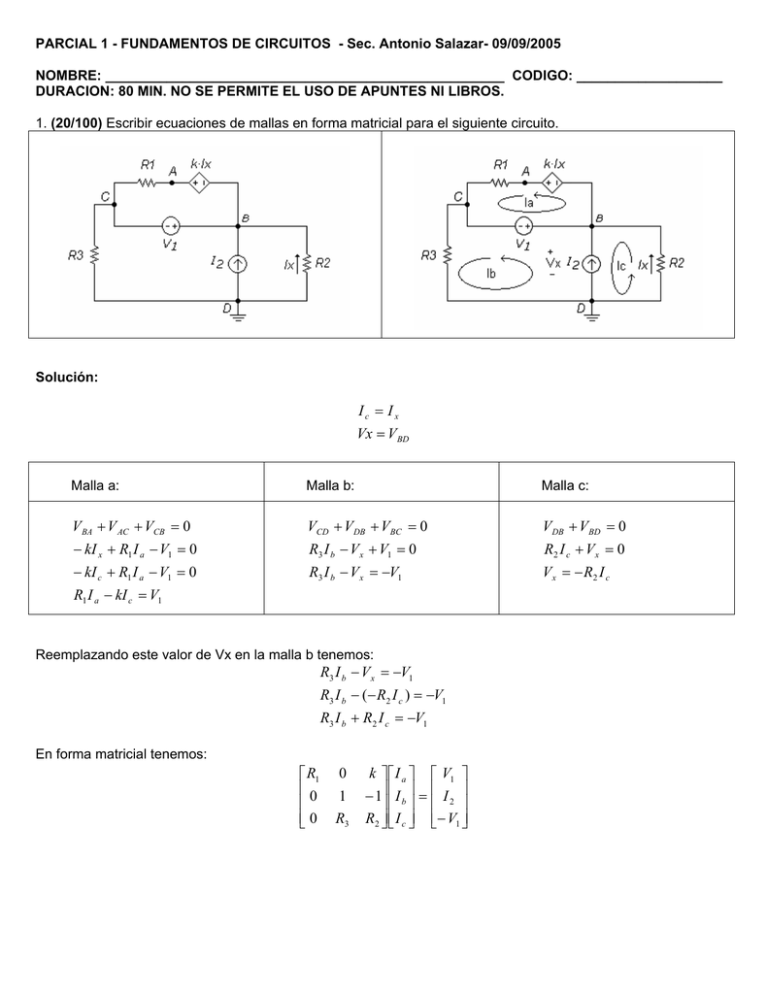
PARCIAL 1 - FUNDAMENTOS DE CIRCUITOS - Sec. Antonio Salazar- 09/09/2005 NOMBRE: ____________________________________________________ CODIGO: ___________________ DURACION: 80 MIN. NO SE PERMITE EL USO DE APUNTES NI LIBROS. 1. (20/100) Escribir ecuaciones de mallas en forma matricial para el siguiente circuito. Solución: Ic = I x Vx = VBD Malla a: Malla b: Malla c: V BA + V AC + VCB = 0 VCD + VDB + VBC = 0 V DB + VBD = 0 − kI x + R1 I a − V1 = 0 R3 I b − V x + V1 = 0 R2 I c + V x = 0 − kI c + R1 I a − V1 = 0 R3 I b − V x = −V1 V x = − R2 I c R1 I a − kI c = V1 Reemplazando este valor de Vx en la malla b tenemos: R3 I b − V x = −V1 R3 I b − (− R2 I c ) = −V1 R3 I b + R2 I c = −V1 En forma matricial tenemos: ⎡ R1 ⎢0 ⎢ ⎢⎣ 0 0 1 R3 k ⎤ ⎡ I a ⎤ ⎡ V1 ⎤ − 1⎥⎥ ⎢⎢ I b ⎥⎥ = ⎢⎢ I 2 ⎥⎥ R2 ⎥⎦ ⎢⎣ I c ⎥⎦ ⎢⎣− V1 ⎥⎦ 2. (20/100) Escribir las ecuaciones de nodos en forma matricial para el siguiente circuito si la tierra está en el nodo C y RAC=2, RBC= 4 y RDC = 1 y k =3. (Ayuda: en tierra también se cumple KCL). Solución: El nodo c es tierra por tanto VC = 0 . Tenemos entonces tres incógnitas y debemos buscar tres ecuaciones. Restricciones: V A − VD = 5 V D − VB = 10 Ya tenemos dos ecuaciones. La tercera sale del nodo C: VDC V BC V AC + + =0 1 4 2 En forma matricial tenemos: ⎡ ⎢1 ⎢0 ⎢1 ⎢ ⎣2 ⎤ − 1⎥ ⎡V A ⎤ ⎡ 5 ⎤ − 1 1 ⎥ ⎢⎢VB ⎥⎥ = ⎢⎢10⎥⎥ ⎥ 1 1 ⎥ ⎢⎣VD ⎥⎦ ⎢⎣ 0 ⎥⎦ 4 ⎦ 0 3. (30/100) Para el siguiente circuito: a. (15) Calcular la potencia disipada por cada elemento. b. (15) Comprobar el principio de conservación de potencia. Solución: Parte a: Primero necesitamos conocer Vx. Haciendo la malla tenemos: V X − (−10) + 5 ⋅ 2 = 0 V X = −20 Haciendo la ecuación del nodo tenemos: I1 + I 2 + I 3 = 0 4V X + I 2 + 3 =0 2 I 2 = 78.5 Cálculo de las potencias absorbidas: P1 = (I R ) R = (2 ) ⋅ 5 = 20W 2 2 P 2 = V ⋅ I = −(−10) ⋅ 2 = 20W P3 = V ⋅ I = −20 ⋅ 2 = −40W P 4 = V ⋅ I = 3 ⋅ 4V X = 3 ⋅ 4(−20) = −240W P5 = V ⋅ I = 3 ⋅ 78.5 = 235.5W P6 = (VR )2 R = (3)2 2 = 4.5W Parte b: 5 ∑ P = 0 = P1 + P2 + P3 + P4 + P5 + P6 = 20 + 20 − 40 − 240 + 235.5 + 4.4 = 0 i =1 i 4. (30/100) Escribir las ecuaciones de nodos en forma matricial para el siguiente circuito. Solución: Tenemos cinco nodos (A-E). Como el nodo e es tierra nos quedan cuatro por calcular: A, B, C y D. Por tanto requerimos cuatro ecuaciones. Las dos fuentes de voltaje nos dan dos restricciones (dos ecuaciones), el Supernodo nos da otra ecuación y la última la sacamos haciendo KCL en el nodo B. Para las restricciones de las fuentes de voltaje tenemos: VC − V A = kI X V D − V E = pI Z = VD Las variables controladoras son: IX = VB − VD R4 IZ = VE − V A − V A = R2 R2 Reemplazando estas dos últimas en las dos primeras tenemos: pI Z = V D = − VA R2 VA + VD = 0 (1) R2 y ⎛ V − VD VC − V A = kI X = k ⎜⎜ B ⎝ R4 VA + Nodo B: ⎞ ⎟⎟ ⎠ k k V B − VC − V D = 0 (2) R4 R4 V A − VB VD − VB VC − VB + + =0 R3 R4 R1 − ⎛1 VA 1 1 ⎞ V V + VB ⎜⎜ + + ⎟⎟ − C − D = 0 (3) R3 ⎝ R1 R3 R4 ⎠ R1 R4 Supernodo: 0 − V A VB − VC VB − V A + + + I1 − I 0 = 0 R2 R1 R3 ⎛ 1 ⎛ 1 1 ⎞ 1 ⎞ VC ⎟⎟ − ⎟⎟ + VB ⎜⎜ + = I 0 − I1 − V A ⎜⎜ + ⎝ R1 R3 ⎠ R1 ⎝ R2 R3 ⎠ (4) En forma matricial las ecuaciones 1 a 4 quedan: p ⎡ ⎢ R2 ⎢ ⎢ 1 ⎢ ⎢ ⎢ − 1 ⎢ R3 ⎢⎛ ⎢⎜ 1 + 1 ⎞⎟ ⎢⎣⎜⎝ R2 R3 ⎟⎠ 0 0 k −1 R4 ⎛ 1 1 1 ⎞ 1 ⎜⎜ + ⎟⎟ − + R1 ⎝ R1 R3 R4 ⎠ ⎛ 1 1 ⎞ 1 ⎟⎟ ⎜⎜ + − R1 ⎝ R1 R3 ⎠ ⎤ 1 ⎥ ⎥ k V − ⎥ ⎡⎢ A ⎤⎥ ⎡⎢ R4 ⎥ V B ⎥⎢ ⎥ = ⎢ 1 ⎥ ⎢V ⎥ ⎢ C − R4 ⎥ ⎢V ⎥ ⎢ I ⎥⎣ D ⎦ ⎣ 0 0 ⎥ ⎥⎦ 0 ⎤ 0 ⎥⎥ 0 ⎥ ⎥ − I1 ⎦








