tema 5.- grafos

TEMA 5.- GRAFOS
5.1.- DEFINICIONES BÁSICAS
Un grafo G es un par (V,E) donde V es un conjunto (llamado conjunto de vértices) y E un
subconjunto de VxV (conjunto de aristas).
Gráficamente representaremos los vértices por puntos y las aristas por líneas que los unen.
Un vértice puede tener 0 o más aristas, pero toda arista debe unir exactamente 2 vértices.
Llamaremos orden de un grafo a su número de vértices, |V|.
Si |V| es finito se dice que el grafo es finito. En este curso estudiaremos los grafos finitos,
centrándonos sobre todo en grafos no dirigidos. También supondremos, a no ser que se diga lo
contrario, que entre dos vértices hay, como mucho, una arista y que toda arista une dos
vértices distintos.
Aristas
Si la arista carece de dirección se denota indistintamente {a,b} o {b,a}, siendo a y b los
vértices que une.
Si {a,b} es una arista, a los vértices a y b se les llama sus extremos.
Vértices
Dos vértices v, w se dice que son adyacentes’ si {v,w}∈A (o sea, si existe una arista entre
ellos)
Llamaremos grado de un vértice al número de aristas de las que es extremo. Se dice que un
vértice es ‘par’ o ‘impar’ según lo sea su grado.
Caminos
Sean x, y ∈ V, se dice que hay un camino en G de x a y si existe una sucesión finita no vacía
de aristas {x,v1}, {v1,v2},..., {vn,y}. En este caso
-
x e y se llaman los extremos del camino
-
El número de aristas del camino se llama la longitud del camino.
-
Si los vértices no se repiten el camino se dice propio o simple.
-
Si hay un camino no simple entre 2 vértices, también habrá un camino simple entre
ellos.
-
Cuando los dos extremos de un camino son iguales, el camino se llama circuito o
camino cerrado.
-
Llamaremos ciclo a un circuito simple
-
Un vértice a se dice accesible desde el vértice b si existe un camino entre ellos. Todo
vértice es accesible respecto a si mismo
Ejemplos de Grafos
1.- Grafo regular: Aquel con el mismo grado en todos los vértices. Si ese grado es k lo
llamaremos k-regular.
Por ejemplo, el primero de los siguientes grafos es 3-regular, el segundo es 2-regular y el
tercero no es regular
2.- Grafo bipartito: Es aquel con cuyos vértices pueden formarse dos conjuntos disjuntos de
modo que no haya adyacencias entre vértices pertenecientes al mismo conjunto
Ejemplo.- de los dos grafos siguientes el primero es bipartito y el segundo no lo es
3.- Grafo completo: Aquel con una arista entre cada par de vértices. Un grafo completo con
n vértices se denota Kn.
A continuación pueden verse los dibujos de K3, K4, K5 y K6
Todo grafo completo es regular porque cada vértice tiene grado |V|-1 al estar conectado con
todos los otros vértices.
Un grafo regular no tiene por qué ser completo.
4.- Un grafo bipartido regular se denota Km,n donde m, n es el grado de cada conjunto
disjunto de vértices.
A continuación ponemos los dibujos de K1,2, K3,3, y K2,5
1.2.- PRIMEROS RESULTADOS SOBRE GRAFOS
Proposición.- La suma de los grados de los vértices es igual al doble del número de aristas
Demostración
Al realizar la suma de los grados de todos los vértices, como cada arista tiene 2 extremos se
cuenta exactamente 2 veces. Por tanto la suma de los grados de los vértices es igual al doble
del número de aristas
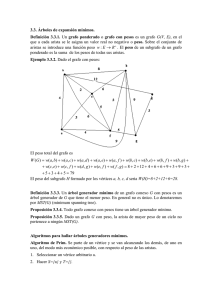
Definición (matriz de adyacencia de un grafo)
Sea G un grafo de orden n. Llamaremos matriz de incidencia de G a la matriz nxn que
llamaremos A = (aij) donde aij = 1 si {i,j}∈A y aij = 0 en otro caso.
La matriz de adyacencia siempre es simétrica porque aij = aji
Ejemplo:
v1
v2
v3
v4
v5
v1
0
1
1
0
0
v2
1
0
1
1
0
v3
1
1
0
1
1
v4
0
1
1
0
0
v5
0
0
1
0
0
v1
v2
v3
v5
v4
Teorema.- Sea G un grafo de n vértices con n > 1 y sea A su matriz de adyacencia. Se cumple
que el valor del coeficiente aijk de la matriz Ak es igual al número de caminos de longitud k con
extremos vi y vj
Demostración
Por inducción en k
Para k = 1 es la definición de A
Supongamos que es cierto para k y vamos a verlo para k+1.
La casilla (i,j) de Ak+1 es el producto de la fila i de Ak por la columna j de A, es decir, si
llamamos (a, b, c,...) a la fila i de Ak y (a’, b’, c’,...) a la columna j de A, entonces la casilla (i,j)
de Ak+1 es aa’ + bb’ +......
El número de caminos de longitud k+1 de i a j que pasan en último lugar por el vértice 1
será 0 si no hay arista de 1 a j o bien coincidirá con el número de caminos de longitud k de i a
1 si existe arista de 1 a j. En resumen, como el número de caminos de i a 1 es el primer
elemento de la fila i de Ak, y el primer elemento de la columna j de A vale 1 ó 0 dependiendo
de si hay o no arista de 1 a j, tendremos que el número de caminos de longitud k+1 de i a j que
pasan en último lugar por el vértice 1 será siempre aa’.
De manera análoga el número de caminos de longitud k+1 de i a j que pasan en último
lugar por el vértice 2 será siempre bb’, y así sucesivamente.
El número total de caminos de longitud k+1 de i a j será la suma de todos los anteriores, es
decir, aa’+bb’+cc’+...., es decir, el elemento (i,j) de la matriz Ak+1.
Nota.- Si existe un camino de longitud m (m ≥ n) entre 2 vértices cualquiera, entonces
existe un camino de longitud ≤ n-1 entre esos dos vértices.
Definición.- Un grafo G se dice conexo si cada par de vértices está unido al menos por un
camino.
Definición.- La relación entre vértices dada por v está relacionado con w si hay un camino
que los une es de equivalencia. Las clases de equivalencia de esta relación se llaman las
componentes conexas del grafo.
Nota.- Un método para comprobar si un grafo es conexo es el siguiente:
- Se halla la matriz de adyacencia y se eleva a la n-1-ésima potencia
- Se calcula la suma de las potencias de A hasta An-1
- Si todos sus elementos son ≠ 0, el grafo es conexo.
Definición.- Una arista de un grafo G se dice de separación si G es conexo pero al suprimir
la arista se divide en dos componentes conexos
Definición.- Dados dos grafos G=(V,E) y G´=(V´,E´), se denomina isomorfismo entre G y G´
a cualquier aplicación biyectiva f:G → G’ tal que si a, b ∈ V, entonces {a,b}∈E ⇔ {f(a),f(b)}∈E
´.
Es decir, es una aplicación biyectiva entre los vértices de V y los de V´ de modo que los
vértices conectados siguen estándolo. En este caso, diremos que G y G´ son isomorfos.
Si G y G’ son isomorfos son matemáticamente iguales y solo varía la apariencia, o sea, que
se mantienen las adyacencias, estructura, caminos, ciclos, nº de vértices, nº de aristas, etc.
4.3.- GRAFOS EULERIANOS Y HAMILTONIANOS
Grafos eulerianos
Llamaremos camino euleriano a un camino que contiene a todas las aristas del grafo,
apareciendo cada una exactamente una vez.
Un ciclo euleriano es un camino euleriano que comienza y acaba en el mismo vértice.
Definición.- Un grafo que admite un ciclo euleriano diremos que es un grafo euleriano.
Ejemplo:
1)
El primero no tiene ciclos ni caminos euleriano,
El segundo tiene ciclo euleriano
2) Si un grafo es isomorfo a un solo ciclo, siempre tiene ciclo euleriano
Proposición.- Si un grafo está formado por dos subgrafos eulerianos unidos al menos por
un vértice y sin aristas en común, entonces es euleriano
Demostración
Empezamos por uno de los vértices en común, v. Partiendo de él podemos recorrer el primer
subgrafo con un ciclo euleriano, volviendo al vértice de partida.
Ahora recorremos el segundo subgrafo con su ciclo euleriano. La unión de estos dos ciclos
vuelve a ser un ciclo que recorre todas las aristas exactamente una vez, por tanto es un ciclo
euleriano de todo el grafo.
Nota.- Lo mismo ocurre con una unión finita en las condiciones anteriores
Teorema.- Un grafo conexo G=(V,A) es euleriano ⇔ todo vértice tiene grado par.
Demostración:
“⇐“ (por inducción en |A|=m)
El menor número posible de aristas es 3. En este caso el grafo es un triángulo que es
euleriano.
Suponemos que el teorema es cierto para grados en las mismas condiciones y con menos de
m aristas. Tenemos un grafo G con todos los vértices de grado par, dado que G es conexo ⇒ ∀v
∈ V, gr(v) > 0. Empiezo por un vértice v cualquiera y voy recorriendo el grafo mientras pueda,
con la condición de no repetir nunca arista.
Si llego a un vértice w que no sea el del principio, puede pasar que no haya pasado antes
por él o que no sea la primera vez que pase por w.
En el primer caso, la única arista elegida es la que haya usado ahora para llegar a w
En el segundo caso, cada vez que haya pasado antes por w habré escogido dos aristas (una
para llegar y otra para salir) y, finalmente, habré escogido una más para llegar esta última vez
a w.
En cualquiera de los dos casos, he cogido un número impar de aristas en w. Como w tiene
grado par, tiene que haber alguna que no haya cogido todavía. En consecuencia, puedo seguir
recorriendo el grafo.
Como el número de aristas es finito, llegará un momento en que tenga que pararme, es
decir, llegará un momento en que al llegar a un vértice no pueda seguir porque ya haya
elegido todas las aristas que había en ese vértice. Por lo que hemos dicho antes, en ese
momento debo estar de vuelta en el vértice v y hemos construido un ciclo.
Consideremos el subgrafo formado por el ciclo anterior que es claramente euleriano.
Si ese subgrafo tiene todas las aristas del grafo, el grafo original coincide con el subgrafo,
por lo que G es euleriano.
En otro caso, consideremos el subgrafo formado por las aristas que no hayamos elegido.
Este subgrafo tiene un número menor de aristas que G. Además, el grado de los vértices ha de
seguir siendo par. En efecto, el grado de los vértices será el grado original (que era par), menos
las aristas que hayamos quitado. Pero, como lo que hemos quitado es un ciclo, el número de
aristas que quitamos en cada vértice es un número par (igual a dos veces el número de
ocasiones en que el ciclo pase por ese vértice). En consecuencia, el grado de cada vértices es
ahora par - par = par. Descomponiendo en componentes conexas, tendremos ahora una unión
disjunta de grafos que, por el principio de inducción, deben de ser eulerianos.
Ahora bien, la unión de estos grafos es G que era conexo, así que deben tener vértices en
común. Pero ya vimos que la unión de grafos eulerianos sin aristas en común y unidos por
vértices es euleriano.
“⇒” Como todas las aristas están una vez y sólo una en el ciclo, el grado de un vértice es el
número de aristas del ciclo que pasan por él. Si recorremos el ciclo, cada vez que pasamos por
un vértice tendremos dos aristas (una de llegada y otra de salida). Por tanto el grado de cada
vértice será dos veces el número de ocasiones que pase por él el ciclo euleriano. En
consecuencia el grado es par
Proposición.- Un grafo conexo tiene un camino abierto euleriano ⇔ tiene exactamente dos
vértices de grado impar.
Demostración
“⇐” Añadimos un nuevo vértice junto con dos aristas que lo unan a los dos vértices que
tenían grado impar. Ahora estos vértices, al haberles añadido una arista a cada uno, tienen
grado par y el nuevo vértice tiene grado 2, por tanto, todos los vértices son de grado par. Por el
teorema anterior, tendremos un ciclo euleriano. Si en dicho ciclo quitamos ahora el vértice y
las dos aristas que habíamos añadido, obtendremos un camino abierto que contiene
exactamente una vez a cada arista de nuestro grafo original.
“⇒” La demostración es similar a la del teorema de Euler.
Algoritmo de Fleury
Si G es un grafo euleriano siempre es posible seguir la siguiente construcción de un circuito
euleriano. Se empieza por un vértice arbitrario y se recorren las aristas arbitrariamente
sometida a dos condiciones:
1) Se borran las aristas a medida que son atravesadas
2) Solo se recorre una arista de separación si no queda otra alternativa
Caminos hamiltonianos
Un camino hamiltoniano es un camino que recorre todos los vértices de un grafo sin pasar
dos veces por el mismo vértice. Si el camino es cerrado se dice un ciclo hamiltoniano
Un grafo G se dice hamiltoniano si tiene un ciclo hamiltoniano.
Nota.- A diferencia de los grafos eulerianos, no hay una caracterización de cuando un grafo
tiene un ciclo o un camino hamiltoniano
Teorema.- Si un grafo es conexo con |V|≥ 3 y para cada par de vértices la suma de sus
grados es mayor o igual que el número de vértices entonces es hamiltoniano.
Problema del vendedor ambulante
En un grafo G con pesos se pretende encontrar un ciclo que pase por todos los vértices de
forma que la suma de los pesos de las aristas escogidas para formar el ciclo sea lo menor
posible.
4.4.­ ÁRBOLES
Definición.- Un grafo se dice un árbol si es conexo y no tiene ciclos.
Ejemplos: Los dos grafos siguientes grafos son árboles:
Mientras que el siguiente no lo es
Nota.- Por tanto, un grafo es un árbol ⇔ entre cada par de vértices existe un camino y sólo
uno.
Definición.- Un grafo se dice un bosque si sus componentes conexas son árboles.
Teorema.- Sea G(V,E) un grafo. Son equivalentes
a) G es un árbol
b) Cada par de vértices distintos de V esta conectado por un único camino.
c) G es conexo y toda arista de G es de separación
d) G no tiene ciclos y |V| = |E| + 1
e) G es conexo y |V| = |E| + 1
f) G no tiene ciclos pero al añadirle una arista a G se crea un único circuito
Demostración
“a⇒b” Por definición de árbol, G es conexo y entre cada par de vértices debe haber, al
menos, un camino. Si hubiese dos caminos distintos uniendo dos vértices, su unión formaría un
ciclo, pero los árboles no tienen ciclos
“b⇒c” Es conexo porque cada par de vértices está conectado por un camino. Una arista es
un camino entre dos vértices, por tanto es el único. Si quito esa arista, ya no hay caminos entre
los vértices que unía y el grafo deja de ser conexo. Por tanto toda arista es de separación.
“c⇒d” G no puede tener ciclos porque las aristas de los ciclos no son de separación
Veamos que |V|=|E|+1 por inducción en |V|
Para |V|=1 hay un único vértice v ⇒ |A| = 0 y |V| = |A| + 1
Supongamos que el teorema es cierto para grafos con menos de n aristas y vamos a verlo
si n = |A|.
Quito una arista e, que será de separación, y el grafo se parte en dos componentes conexas
G1 = (V1, E1) con |V1| < n y G2 = (V2, E2) con |V2| < n.
Por la hipotesis de inducción |V1| = |E1| + 1, |V2| = |E2| + 1, luego |V| = |V1| + |V2| = (|E1| +
+|E2| + 1) + 1 = |E| + 1
“d⇒e” Veamos que G es conexo. Si no lo fuera, lo parto en componentes conexas, G1,..., Gm.
Cada una de ellas es conexa y sin ciclos, por lo que |V1| = |E1| + 1, ..., |Vm| = |Em| + 1. Pero
entonces |V| = |V1| +...+ |Vm| = |E1| + 1 +.....+ |Em| + 1 = |E| + m en vez de ser |E|+1.
“e⇒f” Suponemos que existe un ciclo (con k aristas y k vértices) y vamos a llegar a una
contradicción. Pueden suceder 2 casos
1) k = n, |E| ≥ k = n, n = |V| pero por la hipótesis |V| = |E| + 1 luego |V| > |E|
2) los n - k vértices restantes necesitan al menos otras n - k aristas que les unan con los
demás para que G sea conexo, pero entonces |E| ≥ k + (n - k) = n = |V| pero por hipótesis |V|
= |E| + 1
“f⇒a” Si G no fuese conexo, habría dos vértices entre los que no habría ningún camino.
Entonces al añadir una arista entre ellos no formaríamos ningún ciclo
Definición.- Sea G un grafo, un árbol generador de G es un subgrafo conexo de G que tiene
los mismos vértices que G y no tiene circuitos
Nota.- Un árbol generador se puede crear de 2 modos:
1) Suprimir aristas que no sean de separación
2) Partiendo de los vértices coger aquellas aristas de forma que no creemos ningún
circuito
Supongamos que a cada arista se le asocia un número positivo (su peso). Un árbol
generador se dice de peso mínimo si la suma de los pesos de las aristas que lo componen es lo
menor posible
Para calcular el árbol de peso mínimo existen 2 algoritmos:
-
Kruskal: Se van cogiendo las aristas de menor peso hasta conseguir un árbol de peso
mínimo
-
Prim: Consiste en ir borrando las aristas de mayor peso posible y que no sean aristas
de separación.
Puede haber más de un árbol generador de peso mínimo, pero todos deben tener el mismo
peso.
Definición.- Un árbol con raíz es un árbol con un vértice distinguido llamado raíz.
Si le quitan la raíz quedan árboles con raíz T1,T2,...
En este tipo de árbol los vértices se llaman nodos. Se llama hijo de un nodo al vértice
adyacente que esta más alejado de la raíz que el nodo del que es hijo. Los nodos sin hijos se
llaman hojas.
Un árbol se dice n-ario cuando todos los nodos excepto los terminales tienen a lo sumo n
hijos.
Definición.- Se llama nivel de un vértice al número de aristas que le separan de la raíz. La
raíz tiene nivel 0.
Se llama altura de un árbol al máximo nivel de sus vértices.
4.5.- GRAFOS PLANOS
Definición.- Un grafo se dice plano si admite una representación gráfica en el plano de
modo que dos aristas pueden cortarse únicamente en un vértice.
Una representación gráfica de este tipo se llama un mapa.
Decimos que un mapa es conexo si representa a un grafo conexo.
Ejemplo:
Grafo plano Mapa del grafo plano
Un mapa divide al plano en varias partes llamadas regiones. Cada región de un mapa M está
delimitada por un ciclo si el mapa es conexo. También se cuenta como región la exterior a la
figura.
Ejemplo:
4
1 2
3
Definición.- Se llama grado de una región a la longitud del camino que la bordea.
Dos regiones de un mapa se consideran adyacentes si el circuito que las bordea tiene
alguna arista en común.
Teorema.- La suma de los grados de las regiones de un mapa es igual al doble del número
de aristas del grafo al que representa.
Demostración
Toda arista es frontera simple de 2 regiones o doble de la misma región, con lo que cada una
se cuenta doble.
Ejemplo de frontera doble:
Definición.- Llamaremos pseudomultigrafo dual de un mapa M, a aquel que se construye
asociando un vértice a cada región de M y si una arista es frontera común de dos regiones,
añadimos en el dual una arista uniendo los vértices correspondientes a esas regiones.
Como dos regiones pueden tener más de una arista como frontera común, nos vemos
obligados a permitir que haya más de una arista entre dos vértices. Así mismo, puede haber
aristas que empiecen y terminen en el mismo vértice.
Teorema.- Todo mapa conexo verifica
nº regiones + nº vértices – nº aristas = 2
Demostración:
Sea G un mapa conexo. Por inducción en |E|:
a) Si |E|=0 ⇒ Como es conexo, ha de ser |V|=1, |R|=1. Con lo que claramente se
verifica la fórmula de Euler.
b) Supongamos que |E|= m ≥ 1
Se dan dos casos
1) Si el mapa tiene algún ciclo. Consideremos el subgrafo G' resultante de
suprimir una arista perteneciente a un circuito. G' seguira siendo conexo
porque la arista pertenecía a un circuito y el número de regiones disminuye
en una unidad porque las aristas pertenecientes a un ciclo siempre son
fronteras de dos regiones distintas. Por la hipótesis de inducción, para M'
tenemos que ( R −1) + V − ( E −1) = 2 , luego R + V − E =2
2) Si el grafo no tiene ningún ciclo (es decir, si es un árbol). En este caso |R|=1.
Usando la relación entre el número de vértices y de aristas de un árbol,
tendremos R + V − E =2
Definición.- Una subdivisión elemental de un grafo G es el grafo G' obtenido colocando un
vértice en medio de una arista de G.
Una subdivisión de un grafo G es un grafo obtenido efectuando un número finito de
subdivisiones elementales sucesivas.
Teorema ( de Kuratowski)
Un grafo G es plano ⇔ no contiene ningún subgrafo isomorfo a una subdivisión de K5 o K3,3.
Demostración:
Demasiado complicada para este nivel.
4.6.- COLORACIONES DE GRAFOS
Definición.- Sea G = (V,E) un grafo y C = {1,2,..k} un conjunto de k colores. Una coloración
con k colores del grafo G es una aplicación de f : V → C de modo que si los vértices u, v, son
adyacentes entonces f(u) ≠ f(v).
Se llama número cromático del grafo G al menor k tal que G puede colorearse con k colores
Teorema (de los 4 colores).- El número cromático de un grafo plano es siempre menor o
igual que 4.
Definición.- Un grafo G se dice que es bipartido si se puede colorear con 2 colores
Teorema.- Un grafo es bipartito ⇔ no tiene circuitos de longitud impar.
Demostración
“⇒” Si G es bipartito, los vértices de cada circuito deben ir alternando de un color a otro.
Para que el color del primer y último vértice del circuito no coincidan, el número de aristas del
circuito debe ser par.
“⇐” Podemos suponer que el grafo es conexo.
Elijo un vértice cualquiera v y, dado otro vértice distinto, habrá siempre al menos un camino
que lo una a v.
Además, si hay más de un camino, cada dos de ellos formarán un ciclo que habrá de ser de
longitud par. Por tanto, los dos caminos serán simultáneamente de longitud par o impar. Por
tanto no hay problema en asociar el primer color a aquellos vértices que estén unidos a v por
caminos de longitud impar y dar el segundo color a los demás.
Si hay una arista entre dos vértices, u – w, cualquier camino de v a u se continúa hasta w al
añadir esta arista. Por tanto, si los caminos de v a u eran de longitud par, los de v a w serán de
longitud impar (así mismo, si los caminos a u son de longitud impar, los caminos a w serán de
longitud par). Por tanto la arista une siempre vértices de distinto color.
Definición.- Sea G un grafo bipartido, donde los vértices se descomponen en V 1 y V2 según
su color y siendo el número de vértices en V2 mayor o igual que el de V1. Un emparejamiento
en G es elegir para cada vértice de V1 otro de V2 tal que
1) Cada vértice de V1 está unido por una arista con el correspondiente vértice de V2
2) A dos vértices de V1 distintos les corresponden vértices distintos de V2
Condición de diversidad.- El grafo G cumple la condición de diversidad si, para cualquier
k menor o igual que el número de vértices de V1, y cualquier subconjunto de k vértices de V1,
hay al menos k vértices de V2 unidos a ellos.
Teorema.- En un grafo bipartido hay un emparejamiento si y sólo si se da la condición de
diversidad
Demostración
“⇒” Es obvio, ya que dados k vértices de V1 están unidos, al menos, a los
correspondientes k vértices de V que proporciona el emparejamiento
“⇐” Por inducción en n = número de vértices de V1
Para n = 1 es inmediato
Supongamos que es cierto para grafos en que V1 tiene menos de n vértices y vamos a
verlo para n. Pueden darse dos casos
Caso1.- Hay un número k < n tal que hay k vértices de V1 unidos exactamente a k
vértices de V2.
En este caso partimos el grafo en dos, G1 y G2. En el primero ponemos los k vértices de
V1 con los correspondientes k vértices de V2 y en el segundo ponemos los demás vértices.
Veamos que se da la condición de diversidad en los nuevos grafos por lo que, dado que
en ellos el primer subconjunto de vértices tiene menos de n vértices (tendrán k y n-k,
respectivamente), la hipótesis de inducción nos aseguraría que podíamos hacer
emparejamientos en ellos y, por tanto, en todo el grafo G.
En el primer subgrafo, dado un número r < k, en el grafo inicial había r vértices de V2
unidos a ellos, pero hemos escogido todos los posibles vértices de V 2 unidos a los k vértices de
V1, por tanto también estarán en el grafo G1 y en G1 se da la condición de diversidad.
Cojamos ahora r vértices de V1 que estén en G2. Junto con los k que puse en G1 tendré k
+ r vértices de V1 que, en G, debían estar unidos a k + r vértices de V 2. Como he quitado k
vértices de V2 que puse en G1, en G2 me quedan r vértices de V2 unidos a mis k + r vértices. No
pueden estar unidos a los de G1, por lo que deben estar unidos a los r vértices de G 1 y, una vez
más, se da la condición de diversidad.
Caso 2.- Para cualquier k y cualquier subconjunto de k vértices de V 1 hay al menos k+1
vértices de V2 unidos a ellos.
Elijo un primer vértice de V1 y lo emparejo con otro cualquiera de V2 unido a él. Los quito
y me queda un grafo G’ con n-1 vértices en V 1. Todo se reduce ahora a ver que en G’ también
se da la condición de diversidad y aplicar la hipótesis de inducción.
Cojo k vértices de V1 que estaban unidos al menos a k + 1 vértices de V2. Como en G’ he
quitado un vértice de V2, aún deben estar unidos al menos a k vértices de los que quedan. Por
tanto, en el grafo G’ se sigue dando la condición de diversidad y, por la hipótesis de inducción,
se puede hacer un emparejamiento. Dicho emparejamiento, junto con la primera elección de
emparejar un vértice de V1 con otro de V2, dan el emparejamiento global de G.