EXAMEN DE MATEMÁTICA DISCRETA •
Anuncio

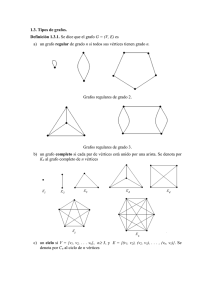
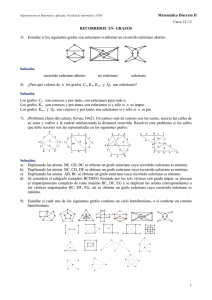
EXAMEN DE MATEMÁTICA DISCRETA • a) Estudia si es verdadera o no la siguiente equivalencia lógica (5 p). " x " y "z P(x,y,z) ! " z " y " x P(x,y,z) b) La física cuántica describe la naturaleza a base de observables clásicos o a base de estados abstractos. Si describe la naturaleza a base de observables clásicos, permite representar las cosas intuitivamente, pero exige la renuncia a la causalidad. Si describe la naturaleza a base de estados abstractos, prohibe la representación intuitiva pero permite conservar la causalidad. Concluir que no es cierto que si la física cuántica representa las cosas intuitivamente, no renuncie a la causalidad. (5 p) • a) Si n es un número que no es múltiplo de 2 y 3 comprueba que (5 p). a.1) n2−1 es divisible por 24. a.2) mcd(2n,4n+3=1. a.3) Calcula las dos últimas cifras de 3343 en base 10. b) Demuestra el teorema de Bezout (5 p). • a) Se consideran números de seis cifras en base diez. ¿En cuántos de ellos aparecen más de tres cifras distintas? (3 p). • ¿Cuántos números hay que sean menores que 106 y en los que aparecen exactamente tres cifras distintas? (7 p). • a) Probar que si x e y sin dos elementos de un álgebra de Boole entonces x = y ! xy' = yx' = 0 ! xy + y'x'=1 (5 p). b) Demuestra que en un álgebra de Boole todo elemento se puede escribir de forma única como suma de átomos (5 p). • a) (5 p). a.1) Demuestra que en un grafo conexo con n aristas hay como mucho n+1 vértices. a.2) Un grafo Kn se dice completo si cada par de vértices está unido por una arista. ¿Para qué valores de n tiene Kn un ciclo euleriano? ¿Y un camino euleriano? b) Demuestra que en un grafo bipartido hay un emparejamiento si y sólo si se da la condición de diversidad (5 p). NOTA.− Cada apartado vale 10 puntos, por lo que la nota definitiva es la suma total dividida por 5. 1