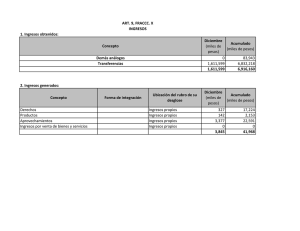
rendimiento-de-operaciones-financieras-problemas

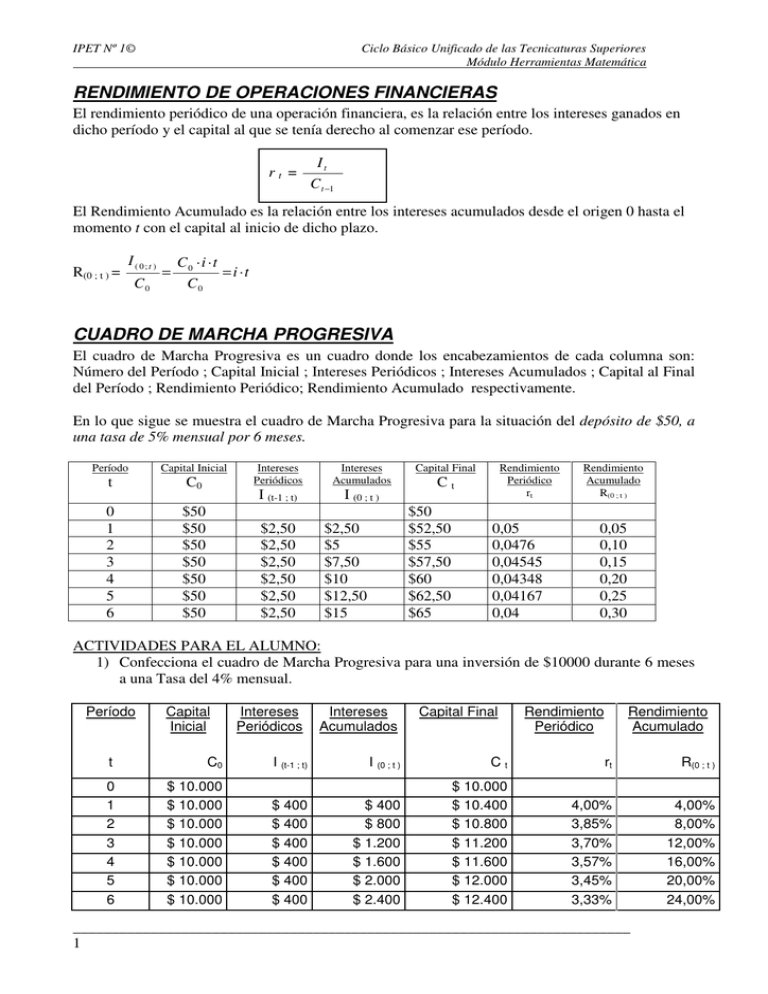
IPET Nº 1©
Ciclo Básico Unificado de las Tecnicaturas Superiores
Módulo Herramientas Matemática
RENDIMIENTO DE OPERACIONES FINANCIERAS
El rendimiento periódico de una operación financiera, es la relación entre los intereses ganados en
dicho período y el capital al que se tenía derecho al comenzar ese período.
rt =
It
C t −1
El Rendimiento Acumulado es la relación entre los intereses acumulados desde el origen 0 hasta el
momento t con el capital al inicio de dicho plazo.
R(0 ; t ) =
I ( 0;t )
C0
=
C0 · i · t
= i ·t
C0
CUADRO DE MARCHA PROGRESIVA
El cuadro de Marcha Progresiva es un cuadro donde los encabezamientos de cada columna son:
Número del Período ; Capital Inicial ; Intereses Periódicos ; Intereses Acumulados ; Capital al Final
del Período ; Rendimiento Periódico; Rendimiento Acumulado respectivamente.
En lo que sigue se muestra el cuadro de Marcha Progresiva para la situación del depósito de $50, a
una tasa de 5% mensual por 6 meses.
Período
Capital Inicial
C0
Intereses
Periódicos
Intereses
Acumulados
t
I (t-1 ; t)
I (0 ; t )
0
1
2
3
4
5
6
$50
$50
$50
$50
$50
$50
$50
$2,50
$2,50
$2,50
$2,50
$2,50
$2,50
Capital Final
Ct
$50
$52,50
$55
$57,50
$60
$62,50
$65
$2,50
$5
$7,50
$10
$12,50
$15
Rendimiento
Periódico
rt
0,05
0,0476
0,04545
0,04348
0,04167
0,04
Rendimiento
Acumulado
R(0 ; t )
0,05
0,10
0,15
0,20
0,25
0,30
ACTIVIDADES PARA EL ALUMNO:
1) Confecciona el cuadro de Marcha Progresiva para una inversión de $10000 durante 6 meses
a una Tasa del 4% mensual.
Período
Capital
Inicial
t
C0
0
1
2
3
4
5
6
$ 10.000
$ 10.000
$ 10.000
$ 10.000
$ 10.000
$ 10.000
$ 10.000
Intereses
Periódicos
I (t-1 ; t)
$ 400
$ 400
$ 400
$ 400
$ 400
$ 400
Intereses
Acumulados
Capital Final
Rendimiento
Periódico
Rendimiento
Acumulado
I (0 ; t )
Ct
rt
R(0 ; t )
$ 400
$ 800
$ 1.200
$ 1.600
$ 2.000
$ 2.400
$ 10.000
$ 10.400
$ 10.800
$ 11.200
$ 11.600
$ 12.000
$ 12.400
4,00%
3,85%
3,70%
3,57%
3,45%
3,33%
4,00%
8,00%
12,00%
16,00%
20,00%
24,00%
________________________________________________________________________
1
IPET Nº 1©
Ciclo Básico Unificado de las Tecnicaturas Superiores
Módulo Herramientas Matemática
FORMULAS:
Período
t
Capital Intereses
Intereses
Capital Final
Inicial Periódicos Acumulados
C0
I (t-1 ; t)
I (0 ; t )
Ct
0
1
$ 10.000
$ 10.000
C0.0,04.1
2
$ 10.000
3
Rendimiento
Periódico
rt
Rendimiento
Acumulado
R(0 ; t )
C0.0,04.1
$ 10.000
C0+C0.0,04.1 $ 400 / $ 10,000
$ 400 / $ 10,000
C0.0,04.1
C0.0,04.2
C0+C0.0,04.2 $ 400 / $ 10,400
$ 800 / $ 10,000
$ 10.000
C0.0,04.1
C0.0,04.3
C0+C0.0,04.3 $ 400 / $ 10,800
$ 1,200 / $ 10,000
4
$ 10.000
C0.0,04.1
C0.0,04.4
C0+C0.0,04.4 $ 400 / $ 11,200
$ 1,600 / $ 10,000
5
$ 10.000
C0.0,04.1
C0.0,04.5
C0+C0.0,04.5 $ 400 / $ 11,600
$ 2,000 / $ 10,000
6
$ 10.000
C0.0,04.1
C0.0,04.6
C0+C0.0,04.6 $ 400 / $ 12,000
$2,400 / $ 10,000
EL CÁLCULO DE LOS TIEMPOS EN FRACCIÓN.
Hay situaciones en los cuales la cantidad de período n no es entero. En esos casos se lo expresa
como número racional no entero. Por ejemplo 5años y 5 meses se lo puede tratar como 5 años +
5
año. Es decir, los 5 meses se transforma como fracción de año. La ventaja es que se puedes
12
adicionar ambas cantidades por estar en una misma unidad de medida.
5
65
Entonces: 5 años +
año =
año.
12
12
ACTIVIDADES PARA EL ALUMNO:
1) ¿Y cómo hace la Señora Díaz si quiere calcular los Intereses y el Monto para tiempos no
exactos o redondos? Describe cómo debe hacer si el tiempo es:
a. Un año y medio.
b. Dos años y tres meses.
c. Nueve meses.
d. 243 días
e. 126 días.
El problema mencionado tiene los siguiente dados: Capital: $1000 e i= 6% anual.
Tanto la fórmula de I y M son las mismas, con la única condición que, como los plazos cambian
debemos hacer compatibles a estos con la tasa de interés, de modo que ambas están en unidades
equivalentes. Es decir, que si expresamos el plazo en años por ejemplo: 1,5 (un año y medio), la
tasa debe estar expresada en años, por ejemplo: 6% anual. Si expresamos el mismo período (1,5
años) en meses, es decir 18 meses la tasa debe estar expresada en meses. Para esto debemos dividir
el valor de la tasa anual por 12: 6%/12 = 0,5%.
Plazos
Un año y medio.
Dos años y tres meses = 27 meses
Nueve meses
243 días
126 días.
Tasa: Partiendo de la tasa anual del 6%
6%
Pasamos la tasa a meses: 6% / 12 = 0.5%
Ídem anterior
Pasamos la tasa a días: 6% / 365 = 0.016%
Ídem anterior
________________________________________________________________________
2
IPET Nº 1©
Ciclo Básico Unificado de las Tecnicaturas Superiores
Módulo Herramientas Matemática
2) Calcular el monto que debe pagarse por una deuda de $20 000 el 22/6 si el pagaré se firmó
el 30/1 del mismo año ( no bisiesto), al 8% anual.
A mediano y largo plazo se usa 360 días en los cálculos, es el tiempo comercial; a corto plazo se
usa 365, es el tiempo real o exacto.
En este caso debemos en primer lugar calcular la cantidad de días que transcurrieron entre las
fechas mencionadas. Para ellos podemos hacer uso de una tabla o utilizar algún programa de
computadora como una planilla de cálculo para obtener el dato.
Entre el 30/Enero y el 22 del junio, transcurrieron 144 días.
La tasa anual debe ser transformada a tasa diaria. Usaremos 360 días: 8% / 360 = 0.022%
Aplicando la fórmula de monto obtenemos:
M = C 0 + C 0 .i.n = $20.000 + $20.000.0,022.144 = $20.000 + $640 = $20.640
Nota: si el año fuera bisiesto, deberíamos agregar un día más, ya que el período comprendido
incluye al mes de febrero.
TASAS PROPORCIONALES:
ACTIVIDAD PARA EL ALUMNO:
1) Completa el cuadro calculando las respectivas tasas proporcionales:
TNA
Cantidad de
15%
períodos por año:
TASA BIMESTRAL
6
15% / 6 = 2,5%
TASA TRIMESTRAL
4
15% / 4 = 3,75%
TASA CUATRIMESTRAL
3
15% / 3 = 5,0%
TASA SEMESTRAL
2
15% / 2 = 7,5%
TASA MENSUAL
12
15% / 12 = 1,25%
TASA DIARIA COMERCIAL
360
15% / 360 = 0,417%
2) Calcula el monto de dos maneras distintas obtenido por capitalización simple de un capital
de $15.300 al 15% de interés anual financiado durante:
Períodos
6 semestres = 36 meses / 12
meses = 3 años
3 trimestres = 9 meses / 12
meses = 0,75 años
5 meses = 5 meses / 12
meses = 0,417 años
120 días = 120 días /
360 días = 0,333 años.
7 cuatrimestres = 7
cuatrimestres / 3
cuatrimestres = 2,333 años
2 bimestres = 2 bimestres /
6 bimestres = 0,333 años
Cálculo del monto, usando tasa anual y llevando todos los
períodos a fracciones de años, con la ecuación de Monto
M= $15.300 · ( 1 + 0,15 · 3 ) = $ 22.185
6 semestres = 3 años
M= $15.300 · ( 1 + 0,15 · 0,75 ) = $ 17.021,25
3 trimestres = 0,75 años
M= $15.300 · ( 1 + 0,15 · 0,417 )= $16.256,25
5 meses = 0,417 años
M = $15.300 · ( 1 + 0,15 · 0,333 ) = $ 16.065
120 días = 0.333 años
M = $15.300 · ( 1 + 0,15 · 2,333 )= $20.655
7 cuatrimestres = 2,333 años
M = $15.300 · ( 1 + 0,15 · 0,333 )= $ 16.065
2 bimestres = 0,333 años
________________________________________________________________________
3
IPET Nº 1©
Ciclo Básico Unificado de las Tecnicaturas Superiores
Módulo Herramientas Matemática
Períodos
6 semestres = 36 meses / 12 meses
= 3 años
3 trimestres = 9 meses / 12 meses
= 0,75 años
5 meses = 5 meses / 12 meses =
0,417 años
120 días = 120 días /
360 días = 0,333 años.
7 cuatrimestres = 7 cuatrimestres
/ 3 cuatrimestres = 2,333 años
2 bimestres = 2 bimestres / 6
bimestres = 0,333 años
Cálculo del monto, usando tasa anual y llevando todos
los períodos a fracciones de años, con la ecuación de
Interés y sumándole el Monto
I = $15.300 · 0,15 · 3 = $ 6.885
M= $15.300 + $ 6.885 = $ 22.185
I= $15.300 · 0,15 · 0,75 = $ 1721,25
M= $15.300 + $ 1721,25 = $ 17.021,25
I= $15.300 · 0,15 · 0,417 = $ 956,25
M= $15.300 + $ 956,25 = $16.256,25
I= $15.300 · 0,15 · 0,333 = $ 765
M = $15.300 + $ 765 = $ 16.065
I= $15.300 · 0,15 · 2,333 = $ 5.355
M = $15.300 + $ 5.355 = $20.655
I = $15.300 · 0,15 · 0,333 = $ 765
M = $15.300 + $ 765 = $ 16.065
3) En la tarjeta de crédito Mastercard, aparece en el sector derecho las siguientes tablas:
TASA EN $
NOMINAL ANUAL
TASA EN U$
38,91
NOMINAL ANUAL
EFECTIVA MENSUAL
26,03
3,20
EFECTIVA MENSUAL
2,14
DIARIA FINANCIACIÓN
0,10700
DIARIA PUNITORIOS
0,05300
Investiga:
a. ¿Cómo se calculó la EFECTIVA MENSUAL?
Tasa Efectiva Mensual ( en $) =
38.91
⋅ 30 = 3,20
365
Tasa Efectiva Mensual ( en U$) =
26,03
⋅ 30 = 2,14
365
b. ¿Cómo se calculó la DIARIA DE FINANCIACIÓN? .
Tasa Diaria de Financiación ( en $) =
38.91
= 0,1070
365
c. Calcula la DIARIA DE FINANCIACIÓN para la TASA EN U$.
Tasa Diaria de Financiación ( en U$) =
26,03
= 0,0713
365
EJERCICIOS PROPUESTOS:
1-¿Qué interés tendrá un capital de inicial de $4000 al 1,5% mensual desde el 12/04 al 18/05 del
mismo año?. Calcula la rentabilidad.
I = ¿?
I = Co · i · n
i = 1,5% mensual
I = $ 4000 · 0.015 · 36/30
n = 36 días (Cantidad de días entre
C0 = $ 4000 · 0.015 · 1,2
el 12/04 y el 18/05.
C0 = $ 72
C0 = $ 4000
________________________________________________________________________
4
IPET Nº 1©
Ciclo Básico Unificado de las Tecnicaturas Superiores
Módulo Herramientas Matemática
Nota: Dividimos los 36 días por 30 para transformar en fracción de mes, ya que la tasa es mensual.
R =
It
$72
=
= 0,018 = 1,8%
$4.000
C t −1
2- Se compra mercadería y, al abonarla 125 días después, se recargan $500 en concepto de intereses
al 1,4% mensual. ¿Cuál es el valor de dicha mercadería en el momento de la compra?
I = $ 500
i = 1,4% mensual
n = 125 días.
C0 = ¿?
I = Co · i · n
$ 500 = Co · 0.014 · 125/30
C0 = $ 500 / 0.014 · 4,167
C0 = $ 8.571,43
3-¿Qué tasa anual de interés fue cargada en un préstamo de $5000, si en 20 días se pagan en
concepto de interés simple $65,75?
I = $ 65,75
i = ¿?
n = 20 días
M = $ 5000
$ 65,75 = $ 5000 · i · 20/30
i = $ 65,75 / $ 5000 · 0,667
i = 0,019725 . 100 = 1,9725% mensual
Tasa Annual = 1,9725% . 12 = 23,67%
Nota: Dividimos los 36 días por 30 para transformar en fracción de mes, ya que la tasa es mensual.
4-¿Cuántos días permanece depositado un capital de $600 al 19,2% nominal anual, si genera un
interés simple del $8?
$8 = $600 . 0,192 · n
C0 = $ 600
n = ¿?
I = $8
i = 19,2% anual
$8 / ($600 . 0.192) = n
n = 0.069 años (ya que la tasa que tomamos es anual)
Para obtener la cantidad de días debemos realizar el siguiente cálculo:
Días = 0,069 años . 365 días/año = 25,65 días
5-Silvana Torrijos compra un automóvil de $10000, pagando la mitad al contado y el resto con un
documento cuyo vencimiento se produce en 20 días desde la fecha de compra. Calcular el valor
nominal del mencionado documento, teniendo en cuenta que se cargaron intereses al 18% nominal
anual.
Valor del automóvil: $ 10000
M = $ 5000 · ( 1 + 0,18 · /365 . 20 )
Contado: 50% - Saldo: $ 5.000
Dividimos la tasa anual por 365 para obtener una tasa diaria.
M = ¿?
M = $ 5000 · ( 1 + 0,00986 ) = $ 5000 · 1,00986
i = 18% anual
M = $ 5049,32
n = 20 días
C0 = $ 5.000
________________________________________________________________________
5
IPET Nº 1©
Ciclo Básico Unificado de las Tecnicaturas Superiores
Módulo Herramientas Matemática
6- Si el negocio STOP promociona la venta de monitores Flat X17 cuyo precio de contado es de
$1.750, pero ofrece la opción de pagarlo en 2 cuotas, una entrega inicial del 50 % y el saldo a 60
días. Esta opción soportará un recargo del 3% sobre el precio de contado, cual es la tasa de interés
real de la operación?¿Porque?
Calculamos el porcentaje sobre el valor del precio de
contado:
Monitor Flat X17 = $ 1.750
Entrega inicial: 50% = $ 875
I = $ 65,75
i = 3%
n = 60 días
M = $ 5000
Recargo = $ 1.750 · 3% = $ 52,50
Y ahora calculamos la tasa de interés:
$52,50 = $ 875 . i . 60/30
i = $52,50 / ( $ 875 . 2)
i = 0,03 = 3% mensual
La tasa de interés es del 3% mensual y no del 1,5%, ya que el cálculo del recargo está hecho sobre
el monto original y no sobre el 50% restante a financiar.
7- Olga Álvarez depositó una suma de dinero durante 90 días al 1,8% mensual. Al finalizar el plazo
su saldo fue $6000. ¿Cuál fue el valor de su depósito inicial? Confecciona el Cuadro de Marcha
progresiva.
M = Co · (1+ i · n)
$ 6000 = Co (1 + 0,018 · 90/30)
C0 = $ 6000 / 1,054
C0 = $ 5.692,60
M = $ 6000
i = 1,8% mensual
n = 90 días
C0 = ¿?
Período
Capital Inicial
Intereses
Periódicos
t
C0
I (t-1 ; t)
0
1
2
3
$ 5.692,60
$ 5.692,60
$ 5.692,60
$ 5.692,60
$ 102,47
$ 102,47
$ 102,47
Intereses
Acumulados
I (0 ; t )
$ 102,47
$ 204,93
$ 307,40
Capital Final
Rendimiento
Periódico
Rendimiento
Acumulado
Ct
rt
R(0 ; t )
$ 5.692,60
$ 5.795,07
$ 5.897,53
$ 6.000,00
1,800%
1,768%
1,737%
1,800%
3,600%
5,400%
8-¿A qué tasa nominal mensual está calculada la financiación de artículos de indumentaria, si se
publica en vidriera una oferta donde a pagar dentro de 20 días la suma total es $200, mientras que
ofreciendo pago al contado piden $180?
C0 = $ 180
Los intereses que deberíamos pagar son:
i = ¿?
I = M - C0 = $ 200 - $ 180 = $ 20
n = 20 días
$ 20 = $ 180 · i · 20/30
M = $ 200
i = $ 20 / ($ 180 · 0,667)
i = $ 20 / ($ 180 · 0,667)
i = 0,1667 = 16,67%
Nota: Dividimos 20 días por 30 para transformar en fracción de mes y obtener una tasa mensual.
________________________________________________________________________
6
IPET Nº 1©
Ciclo Básico Unificado de las Tecnicaturas Superiores
Módulo Herramientas Matemática
9-Una persona invierte $48000 por el plazo de 10 meses, considerando intereses al 2% mensual
aplicable sobre el capital originario.
a) Confecciona el eje de plazos e importes.
0
1
2
3
4
5
6
7
8
9
10
$48.000 $48.960 $49.920 $50.880 $51.840 $52.800 $53.760 $54.720 $55.680 $56.640 $57.600
b) Confecciona el cuadro de marcha progresiva mensual de la operación de inversión
Período
Capital Inicial
Intereses
Periódicos
t
C0
I (t-1 ; t)
0
1
2
3
4
5
6
7
8
9
10
$ 48.000,00
$ 48.000,00
$ 48.000,00
$ 48.000,00
$ 48.000,00
$ 48.000,00
$ 48.000,00
$ 48.000,00
$ 48.000,00
$ 48.000,00
$ 48.000,00
$ 960,00
$ 960,00
$ 960,00
$ 960,00
$ 960,00
$ 960,00
$ 960,00
$ 960,00
$ 960,00
$ 960,00
Intereses
Acumulados
I (0 ; t )
$ 960,00
$ 1.920,00
$ 2.880,00
$ 3.840,00
$ 4.800,00
$ 5.760,00
$ 6.720,00
$ 7.680,00
$ 8.640,00
$ 9.600,00
Capital Final
Rendimiento
Periódico
Rendimiento
Acumulado
Ct
rt
R(0 ; t )
$ 48.000,00
$ 48.960,00
$ 49.920,00
$ 50.880,00
$ 51.840,00
$ 52.800,00
$ 53.760,00
$ 54.720,00
$ 55.680,00
$ 56.640,00
$ 57.600,00
2,000%
1,961%
1,923%
1,887%
1,852%
1,818%
1,786%
1,754%
1,724%
1,695%
2,00%
4,00%
6,00%
8,00%
10,00%
12,00%
14,00%
16,00%
18,00%
20,00%
10-Por la colocación de cierto capital a un interés del 13% anual durante 45 días considerando el
año real me darán $5080,14. ¿Cómo hago para calcular el valor de ese capital?
M = $ 5080,14
i = 13% anual
n = 45 días.
C0 = ¿?
M = Co · ( 1 + i · n )
$ 5080,14 = Co · ( 1 + 0,13 · 45/365 )
C0 = $ 5080,14 / 1,01603
C0 = $ 5.000,00
Nota: Dividimos 45 días por 365 (año real) para transformar en fracción de año, ya que la tasa es
anual.
________________________________________________________________________
7