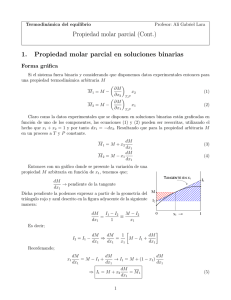
Pregunta 3:

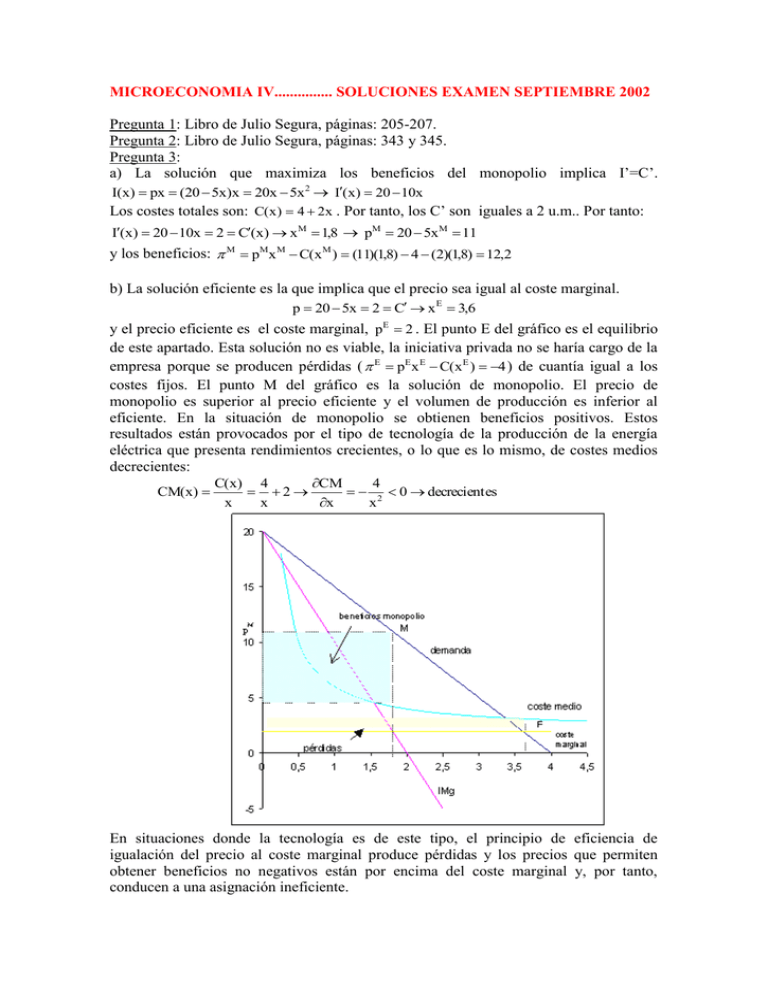
MICROECONOMIA IV............... SOLUCIONES EXAMEN SEPTIEMBRE 2002
Pregunta 1: Libro de Julio Segura, páginas: 205-207.
Pregunta 2: Libro de Julio Segura, páginas: 343 y 345.
Pregunta 3:
a) La solución que maximiza los beneficios del monopolio implica I’=C’.
I(x)  px  (20  5x)x  20x  5x 2  I(x)  20  10x
Los costes totales son: C(x)  4  2x . Por tanto, los C’ son iguales a 2 u.m.. Por tanto:
I(x)  20  10x  2  C(x)  x M  1,8  pM  20  5x M  11
y los beneficios:  M  pMx M  C(x M )  (11)(1,8)  4  (2)(1,8)  12,2
b) La solución eficiente es la que implica que el precio sea igual al coste marginal.
p  20  5x  2  C  x E  3,6
y el precio eficiente es el coste marginal, pE  2 . El punto E del gráfico es el equilibrio
de este apartado. Esta solución no es viable, la iniciativa privada no se haría cargo de la
empresa porque se producen pérdidas (  E  pE x E  C(x E )  4 ) de cuantía igual a los
costes fijos. El punto M del gráfico es la solución de monopolio. El precio de
monopolio es superior al precio eficiente y el volumen de producción es inferior al
eficiente. En la situación de monopolio se obtienen beneficios positivos. Estos
resultados están provocados por el tipo de tecnología de la producción de la energía
eléctrica que presenta rendimientos crecientes, o lo que es lo mismo, de costes medios
decrecientes:
CM(x) 
C(x) 4
CM
4
 2
  2  0  decrecient es
x
x
x
x
En situaciones donde la tecnología es de este tipo, el principio de eficiencia de
igualación del precio al coste marginal produce pérdidas y los precios que permiten
obtener beneficios no negativos están por encima del coste marginal y, por tanto,
conducen a una asignación ineficiente.
c) Una alternativa para que la empresa lance el volumen de producción eficiente y a la
vez cubra sus costes consiste en permitir la discriminación en los precios de venta. Es
decir, tarifas diferentes para cantidades distintas. Desde el punto de vista gráfico se
busca un valor x * tal que el área sombreada B sea igual al área sombreada A. Una
empresa que venda las x * primeras uds. al precio p * y las x E  x * restantes al
precio p E , logra cubrir sus costes y ofrecer la cantidad de producto eficiente x E . Por
tanto se busca el nivel de producción x * que cumpla la siguiente condición:
x* p( x* )  CM ( x* )  ( x E  x* ) CM ( x E )  p( x E )





4

 4



lo que con los datos del problema queda: x* 20  5x*  *  2  (3,6  x* )  2  2
3,6
x



4 *
x  5( x * ) 2  19,1x *  8  0
de donde: 20x *  5( x* ) 2  4  2x*  4 
3,6
y resolviendo esta ecuación de segundo grado se obtienen los valores buscados de
x * posibles (3,344 y 0,479). Por tanto, existen dos posibles soluciones:
- que la empresa venda las 3,344 primeras unidades al precio p*  3,281 y las restantes
x E  x*  0,256 al precio eficiente pE  2 , o ,
- que la empresa venda las 0,479 primeras unidades al precio p*  17,607 y las restantes
x E  x*  3,121al precio eficiente pE  2 .
Pregunta 4:
a) La solución se obtiene a través de la maximización de las funciones de beneficios de
ambas empresas:
 1  10  3x 1  x 2 x 1  x 1  9x 1  3x 12  3x 1 x 2
 2  10  3x 1  x 2 x 2  x 2  9x 2  3x 1 x 2  3x 22
y las condiciones de primer orden para ambos duopolistas son:
 1
dx 2
 9  6x 1  3x 2  3x 1
0
x 1
dx 1
 2
dx 1
 9  3x 1  3x 2
 6x 2  0
x 2
dx 2
Despejando x1 y x 2 de cada una de estas ecuaciones:
x1 
9  3x 2
9  3x 2
x2 
dx
dx
63 2
63 1
dx 1
dx 2
En el modelo de Cournot ambas empresas piensan que aunque ellos varíen su oferta, el
competidor no alterará la suya. Es decir: dx1/dx2= dx2/dx1=0. Por tanto:
x1 
3 1
3 1
 x 2 x 2   x1
2 2
2 2
Resolviendo este sistema obtenemos la solución de Cournot:
x2 
3 13 1 
3 3 1
3/ 4
   x 2   x 2    x 2  x C2 
 1  x 1C
2 22 2 
2 4 4
3/ 4
y el precio del equilibrio de Cournot será: p C  10  3x 1  x 2   4 . Y los beneficios:
 1C   2C  x i (p  c)  1(4 1)  3   TC  6
b) En el modelo de Stackelberg una de las empresas sigue siendo dependiente de la otra,
en este caso la 2. Cree que cuando ella varíe su volumen de producción, su competidora
no cambiará la suya. Es decir, dx 1 / dx 2  0 . La empresa líder adopta una posición
independiente. Cree que la otra variará su producción ante cambios en su volumen de
producción. Es decir: dx 2 / dx 1  0 . Por tanto, la curva de reacción de la empresa
seguidora será la misma que antes:
3 1
 x 1 . Sobre dicha función la empresa líder calculará la variación conjetural:
2 2
dx 2 / dx1  1/ 2 . Introduciendo este valor en la c.p.o. de la empresa 1, tenemos su curva
x2 
de reacción:
x1 
9  3x 2
2
 2 x2
1
3
63
2
El punto de corte de las curvas de reacción proporcionará el equilibrio.
x2 
3 1
3 1
2  3
1
2
1
 x 1    2  x 2    1  x 2  x 2   x S2  0,75
2 2
2 2
3  2
3
3
2
y por tanto: x1S  1,5 ; pS  3,25 ;  1S  1,6875 ,  2S  3,375 y  S   1S   2S  5,0625 .
c) En el modelo en el que ambos se comportan como líderes, cada una de las empresas
cree que la competidora ajustará su producción a la producción esperada de ellas. Por
tanto, ambas variaciones conjeturales son distintas de cero, y su valor concreto se
calcula sobre las curvas de reacción:
x1 
dx
3 1
1
 x2  1  
2 2
dx 2
2
x2 
dx
3 1
1
 x1  2  
2 2
dx 1
2
Sustituyendo estos valores de las variaciones conjeturales en las c.p.o. del problema:
9  3x 2
2
9  3x1
2
 x1  2  x 2
x2 
 x 2  2  x1
dx 2
dx
3
3
63
63 1
dx1
dx 2
2
2 
Resolviendo: x1  2   2  x1   x1I  1,2  x I2 , p  2,8 ;  1I   2I  2,16   I  4,32
3
3 
x1 